Байесовские методы машинного обучения (курс лекций, Д.П. Ветров, Д.А. Кропотов)/Задание 2

Материал из MachineLearning.

Перейти к: навигация, поиск

Перейти к основной странице спецкурса

Начало выполнения задания: 22 ноября 2010 г.
Срок сдачи: 6 декабря 2010 г., 23:59.

Модель Изинга

Прямоугольная система соседства

Треугольная система соседства

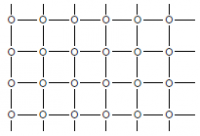
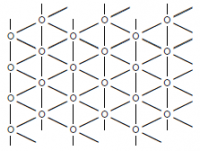
Модель Изинга — математическая модель статистической физики, предназначенная для описания намагничивания материала. Каждой вершине кристаллической решётки (рассматривается двумерный случай) сопоставляется число, называемое спином и равное +1 или −1 («поле вверх»/«поле вниз»). Каждому из $2^N$ возможных вариантов расположения спинов (где N — число атомов решётки) приписывается энергия, состоящая из взаимодействия спинов соседних атомов J и действия внешнего магнитного поля H:
$E(X) = -\left( \frac{1}{2} \sum_{(i,j) \in E} J x_i x_j + \sum_{i=1}^N H_i x_i \right),$
где $x_i$ — переменные, соответствующие спинам, E — система соседства (в данном задании рассматриваются две системы соседства: прямоугольная и треугольная). Вероятность нахождения в каждом конкретном состоянии задается распределением Гиббса:
$P(X) = \frac{1}{Z} \exp{\left( -\beta E(X) \right)}, \qquad \beta = \frac{1}{kT},$
где Z — нормировочная константа, T — температура, k — параметр.

Если $J = 1$ , то вещество называется ферромагнетиком. Если $J = -1$ , то вещество называется антиферромагнетиком.

Задание состоит из двух вариантов. Распределение по вариантам см. на основной странице спецкурса.

Вариант 1

Описание задания

Провести исследование модели Изинга методом Монте-Карло по схеме Гиббса. При этой схеме генерация значения очередного элемента решетки $x_i$ производится по следующим формулам:
$p(x_i = 1 | X_{/\{i\}}) = \frac{1}{1 + \exp(-2\beta b_i)}, \qquad b_i = \sum_{j: (i, j) \in E} J x_j + H_i,$
$p(x_i = -1 | X_{/\{i\}}) = \frac{\exp(-2\beta b_i)}{1 + \exp(-2\beta b_i)}.$

Задание

Пример иллюстрации состояния модели Изинга размера 20 на 20.

Вывести формулы генерации выборки по схеме Гиббса (вывод вставить в отчет).
Реализовать процедуру подсчета математического ожидания и дисперсии энергии (нормированной на количество спинов N), математического ожидания квадрата общей намагниченности модели $\mu = \left(\sum_{i=1}^N x_i \right) / N$ методом Гиббса (с заданным числом итераций) для заданных параметров $\beta$ и внешнего магнитного поля H. (Требования по эффективности реализации для 3-ого курса и выше: 1000 итераций метода Гиббса для решетки размером 20 на 20 и 100 значений параметра $\beta$ должны выполнятся не более 100 секунд. В отчете привести соответствующие замеры времени работы кода.)
Построить графики зависимости от температуры для треугольной и четырехугольной систем соседства, ферромагнетика и антиферромагнетика (всего 4 модели). Проинтерпретировать полученные результаты (в частности идентифицировать, локализовать и изучить фазовый переход). Для построения графиков использовать следующие значения параметров:
- размер решетки 20 на 20 (N = 400);
- $k = 1$ ;
- 10000 итераций метода Гиббса для каждой из температур;
- для ферромагнетика $J = 1$ , для антиферромагнетика $J = -1$ ;
- внешнее магнитное поле $H_i = 0$ ;
- температуры T = 0.5 : 0.1 : 10.
Для ферромагнетика с четырехугольной системой связности отобразить характерные отдельные конфигурации $X$ (см. рис.) в зависимости от температуры (низкая температура, окрестность фазового перехода, высокая температура). Проинтерпретировать результаты. Рассмотреть как минимум по одному примеру для не менее, чем пяти разных значений температур. Параметры генерации те же, что и в пункте 3.
Исследовать влияние константного внешнего магнитного поля на фазовый переход в ферромагнетике с прямоугольной системой соседства. Привести соответствующие графики. Параметры модели взять такие же, как в пункте 3.
Выполнить пункт 4 в присутствии внешнего магнитного поля со следующей структурой: на половине решетки H = 1, на другой половине H = -1.
Сравнить результаты применения метода Монте-Карло с результатами применения вариационного подхода. Рассмотреть ферромагнетик с прямоугольной системой соседства. Реализацию вариационного подхода взять у товарища, выполняющего вариант 2. Привести графики математического ожидания и дисперсии энергии, корня из математического ожидания намагниченности в одних осях для двух подходов.

Оформление задания

Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «Задание 2 <Номер_группы> <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Внимание: задания, в которых прототипы реализованных функций не будут удовлетворять предъявляемым требованиям, рассматриваться не будут!

В качестве программной среды реализации настоятельно рекомендуется использовать MATLAB. Тем не менее, никаких ограничений на выбор среды реализации не накладывается.

Присланный вариант задания должен содержать в себе:

ФИО исполнителя, номер группы и номер варианта задания.
Текстовый файл в формате PDF, содержащий описание проведенных исследований.
Все исходные коды с необходимыми комментариями.
Дополнительные комментарии или материалы, если необходимо.

Исходные коды должны включать в себя реализацию метода Гиббса для прямоугольной и треугольной систем соседств в виде отдельных функций (отдельных m-файлов). Прототипы функций имеют следующий вид:

Метод Гиббса

[E, magnet, samples] = generateIsing4(vS, hS, J, H, iter, betaAll) — прямоугольная система соседства

[E, magnet, samples] = generateIsing6(vS, hS, J, H, iter, betaAll) — треугольная система соседства

ВХОД

vS — размер решетки по вертикали;

hS — размер решетки по горизонтали;

J — параметр модели J;

H — внешнее магнитное поле, матрица размера vS на hS;

iter — количество итераций метода Гиббса;

betaAll — вектор значений параметра $\beta$ (в MatLab матрица размера 1 x $\beta_0$ ).

ВЫХОД

E — значения энергий на один спин $\left(\frac{1}{N}E\right)$ для каждой температуры и итерации, массив размера iter на $\beta_0$ ;

magnet — значения магнетизации $\left(\mu\right)$ для каждой температуры и итерации, массив размера iter на $\beta_0$ ;

samples — примеры конфигураций $X$ для всех температур, массив размера vS на hS на $\beta_0$ .