Статистические свойства МНК-оценок коэффициентов регрессии
Материал из MachineLearning.
Tatira (Обсуждение | вклад)
(Новая: Для того, чтобы '''МНК-оценки коэффициентов [[многомерная линейная регре...)
К следующему изменению →
Версия 22:12, 28 января 2009
Для того, чтобы МНК-оценки коэффициентов многомерной регрессии обладали полезными статистическими свойствами необходимо выполнение ряда предпосылок относительно оцениваемой регрессионной модели, называемых Основными Положениями.
Основные Положения
- ОП.0
(модель линейна по параметрам);
- ОП.1
- детерминированная
матрица,
(признаки линейно независимы);
- ОП.2 Регрессионные остатки
- 2.1. одинаково распределены;
- 2.2.
(модель несмещенная);
- 2.3.
(гомоскедастичность);
- 2.4.
(некореллированность).
- Дополнительное Предположение 3 (ДП3):
,
- т.е регрессионные остатки имеют нормальное распределение
, где
- единичная матрица размера
.
Свойства МНК-оценок без предположения о нормальности
Теорема Гаусса-Маркова. Пусть выполнены основные положения 0-2. Тогда оценка полученная по методу наименьших квадратов является эффективной в классе линейных (вида
) несмещенных оценок (Best Linear Unbiased Estimator, BLUE).
Исходя из этой теоремы можно выделить несколько основных свойств МНК-оценки
- Линейность:
-
где
-
- Несмещенность:
- Матрица ковариации равна:
- МНК-оценка
эффективна.
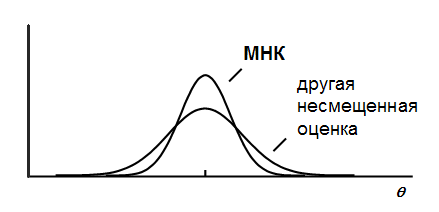
Итак, теорема Гаусса-Маркова утверждает, что любая другая линейная несмещенная оценка будет иметь большую дисперсию, чем МНК-оценка:
Нетрудно показать, что для любого вектора оценка
будет обладать теми же свойствами, что и МНК-оценка
. Поэтому:
- если взять
то получим что
- несмещенная, эффективная оценка
- если
то
- несмещенная, эффективная оценка