Метод потенциальных функций
Материал из MachineLearning.
(→Выбор параметров) |
|||
| Строка 24: | Строка 24: | ||
== Выбор параметров == | == Выбор параметров == | ||
| - | + | Как мы уже заметили, в основной формуле метода потенциальных функций используются две группы параметров: | |
| + | * <tex>\gamma(x_i)</tex> – «потенциал» объекта <tex>x_i \in X^l</tex>, <tex>i=\overline{1,l}</tex> | ||
| + | * <tex>h(x_i)</tex> – «ширина потенциала» объекта <tex>x_i \in X^l</tex>, <tex>i=\overline{1,l}</tex> – своеобразный аналог ширины окна в [[Метод парзеновского окна|методе парзеновского окна]]. | ||
| - | + | Ниже приведён алгоритм, который позволяет «обучать» параметры <tex>(\gamma(x_1), \dots, \gamma(x_n))</tex>, то есть подбирать их значения по обучающей выборке <tex>X^l</tex>. | |
| - | + | Вход: Обучающая выборка из <tex>l</tex> объектов – <tex>X^l</tex>. <br /> | |
| - | + | Выход: Значения параметров <tex>\gamma_i \equiv \gamma(x_i)</tex> для <tex>i=\overline{1,l}</tex> <br /> <br /> | |
| - | + | 1. Начало. Инициализация: <tex>\gamma_i:=0</tex> для всех <tex>i=\overline{1,l}</tex>; <br /> | |
| - | + | 2. Повторять {<br /> | |
| - | + | 3. Выбрать очередной объект <tex>x_i</tex> из выборки <tex>X^l</tex>;<br /> | |
| - | + | 4. Если <tex>a(x_i) \not= y_i</tex>, то <tex>\gamma_i:=\gamma_i+1</tex>;<br /> | |
| + | 5. } пока <tex>Q(a,X^l) > \varepsilon</tex> (то есть пока процесс не стабилизируется).<br /> | ||
Версия 11:06, 3 января 2010
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |
Метод потенциальных функций - метрический классификатор, частный случай метода ближайших соседей.
Введение
Общая идея метода иллюстрируется на примере электростатического взаимодействия элементарных частиц. Известно, что потенциал электрического поля элементарной заряженной частицы в некоторой точке пространства пропорционален отношению заряда частицы (Q) к расстоянию до частицы (r):
Основная формула
, где
-
– потенциальная функция. Константа
вводится чтобы избежать проблем с делением на ноль и берётся произвольно (например,
).
-
– расстояние от объекта u до i-того ближайшего к u объекта –
.
-
– параметр;
-
– параметр.
Вопрос о выборе параметров (их 2l). Необходимо обучать их по выборке.
Выбор параметров
Как мы уже заметили, в основной формуле метода потенциальных функций используются две группы параметров:
-
– «потенциал» объекта
,
-
– «ширина потенциала» объекта
,
– своеобразный аналог ширины окна в методе парзеновского окна.
Ниже приведён алгоритм, который позволяет «обучать» параметры , то есть подбирать их значения по обучающей выборке
.
Вход: Обучающая выборка изобъектов –
.
Выход: Значения параметровдля
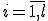
1. Начало. Инициализация:для всех
;
2. Повторять {
3. Выбрать очередной объектиз выборки
;
4. Если, то
;
5. } пока(то есть пока процесс не стабилизируется).

