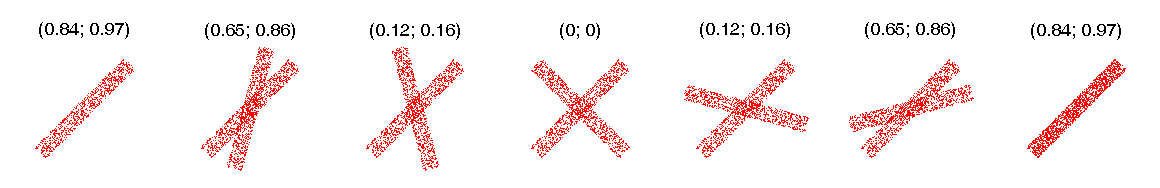Коэффициент корреляции Спирмена

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Содержание

1 Определение
2 Статистическая проверка наличия корреляции
3 Примеры
4 Связь коэффициентов корреляции Спирмена и Пирсона
5 Связь коэффициентов корреляции Спирмена и Кенделла
6 История
7 Примечания
8 Литература
9 Ссылки

Коэффициент корреляции Спирмена (Spearman rank correlation coefficient) — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.

Определение

Заданы две выборки $x = (x_1,\ldots,x_n),\;\; y = (y_1,\ldots,y_n)$ .

Вычисление корреляции Спирмена:

Коэффициент корреляции Спирмена вычисляется по формуле:

$\rho=1-\frac{6}{n(n-1)(n+1)}\sum_{i=1}^n(R_i-S_i)^2$ ,^[1] где $R_i$ - ранг наблюдения $x_i$ в ряду $x$ , $S_i$ - ранг наблюдения $y_i$ в ряду $y$ .

Коэффициент $\rho$ принимает значения из отрезка $[-1;\;1]$ . Равенство $\rho=1$ указывает на строгую прямую линейную зависимость, $\rho=-1$ на обратную.

Случай совпадающих наблюдений:

При наличии связок коэффициент корреляции Спирмена следует вычислять следующим образом:

$\rho = \frac{\sum_{i=1}^n{(R_i-(n+1)/2)(S_i-(n+1)/2)}}{n(n-1)(n+1)-\Delta},$ ^[1]

где $\Delta=\frac{1}{2}\sum_{l=1}^q{u_i^x((u_i^x)^2-1)+\frac{1}{2}\sum_{i=1}^{f}{u_i^y((u_i^y)^2-1)}}$ .

Здесь $q$ и $f$ — количество связок в выборках $x$ и $y$ , $u^x_1, \ldots, u^x_q$ , $u^y_1, \ldots, u^y_f$ — их размеры. Для элементов связок вычисляется средний ранг.

Обоснование критерия Спирмена:

Статистикой критерия Спирмена служит коэффициент корреляции Пирсона $\rho$ ранговых наборов $(R_1 \ldots R_n)$ и $(S_1 \ldots S_n)$ . Он определяется следующей формулой:

$\rho = \sum_{i=1}^n(R_i-\bar R)(S_i-\bar S) \left/ \left[ \sum_{i=1}^n(R_i-\bar R)^2 \sum_{i=1}^n(S_i-\bar S)^2 \right] ^ {1/2}.$ В этой формуле $\bar R = \bar S = \frac1n\sum_{i=1}^n i = \frac{n+1}{2}$ .

Воспользовавшись тем, что $\sum_{i=1}^ni^2 = \frac{n(n+1)(2n+1}{6}$ , получим:

$\sum_{i=1}^n(R_i-\bar R)^2 = \sum_{i=1}^n(S_i-\bar S)^2 = \sum_{i=1}^n\left( i - \frac{n+1}{2} \right)^2 = \frac{n(n-1)(n+1)}{12}$ .

Переставив пары $(R_i,\ S_i)$ в порядке возрастания первой компоненты, получим набор $(1,\ T_1) \ldots (n,\ T_n)$ . Тогда перепишем коэффициент корреляции Спирмена в виде:

$\rho = \frac{12}{n(n-1)(n+1)}\sum_{i=1}^n \left( i - \frac{n+1}{2} \right) \left( T_i - \frac{n+1}{2} \right)$ .

Таким образом, $\rho$ - линейная функция от рангов $T_i$ . Правую часть равенства можно представить в следующем виде:^[1]

$\rho = 1 - \frac{6}{n(n-1)(n+1)}\sum_{i=1}^n(i - T_i)^2 = 1 - \frac{6}{n(n-1)(n+1)}\sum_{i=1}^n \left( R_i - S_i \right)^2,$ который наиболее удобен для вычислений.

Статистическая проверка наличия корреляции

Нулевая гипотеза $H_0$ : Выборки $x$ и $y$ не коррелируют ( $\rho = 0$ ).

Статистика критерия: $\rho.$

Критерий (при уровне значимости $\alpha$ ):

Против альтернативы $H_1:\; \rho\ >\ 0$ :

если $\rho$ больше табличного значения критерия Спирмена $p$ ^[1] с уровнем значимости $\alpha/2$ , то нулевая гипотеза отвергается.

Асимптотический критерий:

Критическая область критерия Спирмена.

Рассмотрим центрированную и нормированную статистику Спирмена:

$\tilde{\rho} = \frac{\rho}{\sqrt{D_{\rho}}},$ , где $D_{\rho}=\frac{1}{n-1}$ .

Нулевая гипотеза отвергается (против альтернативы $H_2$ — $\left| \rho \right|\ >\ 0$ ), если:

$\left|\tilde{\rho}\right| \ge \Phi_{1-\alpha/2}$ ,^[1]^[1] где $\Phi_{1-\alpha}$ есть $(1-\alpha)$ -квантиль стандартного нормального распределения.

Аппроксимация удовлетворительно работает, начиная с $n\geq 50$ .^[1]

Поправка:^[1]^[1]

В 1978 году Р. Иман и У. Коновер предложили следующую поправку, значительно повышающую точность аппроксимации. Она использует линейную комбинацию нормальной и стьюдентовской квантилей. Положим:

$\tilde{\rho} ^{*} = \frac12 \tilde{\rho} \left[ \sqrt{n-1} + \sqrt{\frac{n-2}{1 - (\tilde{\rho})^2}} \right]$ .

Гипотеза $H_0$ отвергается в пользу альтернативы $H_1\ (\rho\ >\ 0)$ , если $\tilde{\rho} ^{*} \ge (x_{1-\alpha}+y_{1-\alpha})/2$ , где $x_{1-\alpha},\; y_{1-\alpha}$ обозначают соответственно квантили уровня $(1-\alpha)$ стандартного нормального распределения и распределения Стьюдента с $n-2$ степенями свободы.

Примеры

Ниже приведены примеры вычисления корреляций Кенделла и Спирмена. Значения коэффициентов указаны над каждым изображением в виде $(\tau,\ \rho)$ , где $\tau$ - корреляция Кенделла, $\rho$ - Спирмена. Заметно, что в большинстве случаев $\left| \rho \right|\ >\ \left| \tau \right|$ . Объяснение этого эффекта приводится ниже.

Направление линейной зависимости

Корреляции Кенделла и Спирмена. Нормальные сгущения.

Коэффициенты корреляции реагируют на изменение направления и зашумлённость линейной зависимости между переменными.

Наклон линейного тренда

Корреляции Кенделла и Спирмена. Вращающаяся полоса.

Коэффициенты корреляции реагируют на изменение направления, но не реагируют на изменение наклона тренда. На первом, четвёртом и седьмом рисунках дисперсия одной из переменных близка к нулю, поэтому не удаётся зафиксировать факт линейной зависимости.

Нелинейная зависимость

Корреляции Кенделла и Спирмена. Нелинейная зависимость.

Корреляции Кенделла и Спирмена не отражают меры нелинейной зависимости между переменными.

Линейная и нелинейная зависимости

На каждой из приведённых ниже иллюстраций осуществляется переход от линейной зависимости к нелинейной. Коэффициенты корреляции Кенделла и Спирмена реагируют на это одинаковым образом.

Корреляции Кенделла и Спирмена. Перекрещенные полосы.

Корреляции Кенделла и Спирмена. Расширяющаяся полоса.

Корреляции Кенделла и Спирмена. Синусоида с переменной амплитудой.

По мере смены линейной зависимости нелинейной значения коэффициентов корреляции падают.

Связь коэффициентов корреляции Спирмена и Пирсона

В случае выборок из нормального распределения коэффициент корреляции Спирмена $\rho$ может быть использован для оценки коэффициента корреляции Пирсона $r$ по формуле:

$r=2sin{\frac{\pi}{6}\rho}$ .^[1]

Связь коэффициентов корреляции Спирмена и Кенделла

Выборкам $x$ и $y$ соответствуют последовательности рангов:

$R_x=(R_{x_1},\ldots,R_{x_n})$ , где $R_{x_i}$ — ранг $i$ -го объекта в вариационном ряду выборки $x$ ;

$R_y=(R_{y_1},\ldots,R_{y_n})$ , где $R_{y_i}$ — ранг $i$ -го объекта в вариационном ряду выборки $y$ .

Проведем операцию упорядочивания рангов.

Расположим ряд значений $x_i$ в порядке возрастания величины: $x_1\leq x_2\leq\cdots\leq x_n$ . Тогда последовательность рангов упорядоченной выборки $x$ будет представлять собой последовательность натуральных чисел $1,2,\cdots,n$ . Значения $y$ , соответствующие значениям $x$ , образуют в этом случае некоторую последовательность рангов $T=(T_1,\cdots,T_n)$ :

$(R_{x_i},\;R_{y_i})\rightarrow^{sort} (i,\;T_i),\; i=1,\cdots,n$ .

Коэффициент корреляции Кенделла $\tau$ и коэффициент корреляции Спирмена $\rho$ выражаются через ранги $T_i,\; i=1,\cdots,n$ следующим образом:

$\rho=1-\frac{12}{n^3-n}\sum_{i<j}{(j-i)[T_i\ >\ T_j]};$

$\tau=1-\frac{4}{n^2-1}\sum_{i<j}[T_i\ >\ T_j];$

Заметно, что в случае $\rho$ инверсиям придаются дополнительные веса $(j-i)$ , таким образом $\rho$ сильнее реагирует на несогласие ранжировок, чем $\tau$ . Этот эффект проявляется в приведённых выше примерах: в большинстве из них $\left| \rho \right|\ >\ \left| \tau \right|$ .

Утверждение.^[1] Если выборки $x$ и $y$ не коррелируют (выполняется гипотеза $H_0$ ), то величины $\rho$ и $\tau$ сильно закоррелированы. Коэффициент корреляции между ними можно вычислить по формуле:

$corr(\rho,\;\tau)=\frac{2n+2}{\sqrt{4n^2+10n}}$ .

История

Критерий был предложен британским психологом Чарльзом Эдвардом Спирменом в 1904 году.

Примечания

Литература

Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 626-628 с.
Лагутин М. Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003. — 343-345 с.
Лапач С. Н., Чубенко А. В., Бабич П. Н. Статистика в науке и бизнесе. — Киев: Морион, 2002. — 182-184 с.

Ссылки

Ранговая корреляция
Коэффициент корреляции Кенделла — другой способ расчёта ранговой корреляции.
Коэффициент корреляции Пирсона
Коэффициент корреляции — статья в русскоязычной Википедии.
Spearman rank correlation coefficient — статья в англоязычной Википедии.

Данная статья является непроверенным учебным заданием.

Студент: Участник:Василий Ломакин

Преподаватель: Участник:Vokov

Срок: 31 декабря 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB%D1%8F%D1%86%D0%B8%D0%B8_%D0%A1%D0%BF%D0%B8%D1%80%D0%BC%D0%B5%D0%BD%D0%B0»

Категории: Прикладная статистика | Энциклопедия анализа данных | Корреляционный анализ | Непроверенные учебные задания

@@ Строка 1: / Строка 1: @@
 {{TOCright}}
+'''Коэффициент корреляции Спирмена''' (Spearman rank correlation coefficient) — мера линейной связи между случайными величинами. Корреляция Спирмена является [[Ранговая корреляция|ранговой]], то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.
+==Определение==
 Заданы две выборки <tex>x = (x_1,\ldots,x_n),\;\; y = (y_1,\ldots,y_n)</tex>.
-Обозначим через <tex>L_x</tex> — число [[вариационный ряд|связок]] в выборке <tex>x</tex>;
+'''Вычисление корреляции Спирмена:'''
-: <tex>T_{x_l}</tex> — число объектов в <tex>l</tex>-ой связке, <tex>l=1,\ldots,L_x</tex>;
-: <tex>L_y</tex> — число [[вариационный ряд|связок]] в выборке <tex>y</tex>;
+Коэффициент корреляции Спирмена вычисляется по формуле:
-: <tex>T_{y_l}</tex> — число объектов в <tex>l</tex>-ой связке, <tex>l=1,\ldots,L_y</tex>;
+:<tex>\rho=1-\frac{6}{n(n-1)(n+1)}\sum_{i=1}^n(R_i-S_i)^2</tex>,<ref>Лагутин М. Б. Наглядная математическая статистика. — 343 с.</ref> где <tex>R_i</tex> - ранг наблюдения <tex>x_i</tex> в ряду <tex>x</tex>, <tex>S_i</tex> - ранг наблюдения <tex>y_i</tex> в ряду <tex>y</tex>.
+Коэффициент <tex>\rho</tex> принимает значения из отрезка <tex>[-1;\;1]</tex>. Равенство <tex>\rho=1</tex> указывает на строгую прямую линейную зависимость, <tex>\rho=-1</tex> на обратную.
+'''Случай совпадающих наблюдений:'''
+При наличии [[Вариационный ряд|связок]] коэффициент корреляции Спирмена следует вычислять следующим образом:
+:<tex>\rho = \frac{\sum_{i=1}^n{(R_i-(n+1)/2)(S_i-(n+1)/2)}}{n(n-1)(n+1)-\Delta},</tex><ref>Лапач С. Н. Статистика в науке и бизнесе. — 182 с.</ref>
+:где <tex>\Delta=\frac{1}{2}\sum_{l=1}^q{u_i^x((u_i^x)^2-1)+\frac{1}{2}\sum_{i=1}^{f}{u_i^y((u_i^y)^2-1)}}</tex>.
+:Здесь <tex>q</tex> и <tex>f</tex> — количество связок в выборках <tex>x</tex> и <tex>y</tex>, <tex>u^x_1, \ldots, u^x_q</tex>, <tex>u^y_1, \ldots, u^y_f</tex> — их размеры. Для элементов связок вычисляется [[Вариационный ряд|средний ранг]].
+'''Обоснование критерия Спирмена:'''
+Статистикой критерия Спирмена служит [[Коэффициент корреляции Пирсона|коэффициент корреляции Пирсона]] <tex>\rho</tex> ранговых наборов <tex>(R_1 \ldots R_n)</tex> и <tex>(S_1 \ldots S_n)</tex>. Он определяется следующей формулой:
+:<tex>\rho = \sum_{i=1}^n(R_i-\bar R)(S_i-\bar S) \left/ \left[ \sum_{i=1}^n(R_i-\bar R)^2 \sum_{i=1}^n(S_i-\bar S)^2 \right] ^ {1/2}.</tex> В этой формуле <tex>\bar R = \bar S = \frac1n\sum_{i=1}^n i = \frac{n+1}{2}</tex>.
+Воспользовавшись тем, что <tex>\sum_{i=1}^ni^2 = \frac{n(n+1)(2n+1}{6}</tex>, получим:
+:<tex>\sum_{i=1}^n(R_i-\bar R)^2 = \sum_{i=1}^n(S_i-\bar S)^2 = \sum_{i=1}^n\left( i - \frac{n+1}{2} \right)^2 = \frac{n(n-1)(n+1)}{12}</tex>.
+Переставив пары <tex>(R_i,\ S_i)</tex> в порядке возрастания первой компоненты, получим набор <tex>(1,\ T_1) \ldots (n,\ T_n)</tex>. Тогда перепишем коэффициент корреляции Спирмена в виде:
+:<tex>\rho = \frac{12}{n(n-1)(n+1)}\sum_{i=1}^n \left( i - \frac{n+1}{2} \right) \left( T_i - \frac{n+1}{2} \right)</tex>.
+Таким образом, <tex>\rho</tex> - линейная функция от рангов <tex>T_i</tex>. Правую часть равенства можно представить в следующем виде:<ref>Лагутин М. Б. Наглядная математическая статистика. — 354 с., задача 3.</ref>
+:<tex>\rho = 1 - \frac{6}{n(n-1)(n+1)}\sum_{i=1}^n(i - T_i)^2 = 1 - \frac{6}{n(n-1)(n+1)}\sum_{i=1}^n \left( R_i - S_i \right)^2,</tex> который наиболее удобен для вычислений.
+==Статистическая проверка наличия корреляции==
+'''[[Нулевая гипотеза]]''' <tex>H_0</tex>: Выборки <tex>x</tex> и <tex>y</tex> не коррелируют (<tex>\rho = 0</tex>).
+'''Статистика критерия:''' <tex>\rho.</tex>
+'''Критерий''' (при [[уровень значимости|уровне значимости]] <tex>\alpha</tex>):
+Против альтернативы <tex>H_1:\; \rho\ >\ 0</tex>:
+: если <tex>\rho</tex> больше табличного значения критерия Спирмена <tex>p</tex><ref>Лагутин М. Б. Наглядная математическая статистика. — 455 с.</ref> с уровнем значимости <tex>\alpha/2</tex>, то нулевая гипотеза отвергается.
+'''Асимптотический критерий:'''
+[[Изображение:Standard_Normal_Density_-_Double-sided_Critical_Area.png|thumb|Критическая область критерия Спирмена.]]
+Рассмотрим центрированную и нормированную статистику Спирмена:
+:<tex>\tilde{\rho} = \frac{\rho}{\sqrt{D_{\rho}}},</tex>, где <tex>D_{\rho}=\frac{1}{n-1}</tex>.
+Нулевая гипотеза отвергается (против альтернативы <tex>H_2</tex> — <tex>\left| \rho \right|\ >\ 0</tex>), если:
+: <tex> \left|\tilde{\rho}\right| \ge \Phi_{1-\alpha/2} </tex>,<ref>Кобзарь А. И. Прикладная математическая статистика. — 627 с.</ref><ref>Лагутин М. Б. Наглядная математическая статистика. — 344 с.</ref> где <tex>\Phi_{1-\alpha}</tex> есть <tex>(1-\alpha)</tex>-[[квантиль]] стандартного нормального распределения.
+Аппроксимация удовлетворительно работает, начиная с <tex>n\geq 50</tex>.<ref>Лагутин М. Б. Наглядная математическая статистика. — 344 с.</ref>
+'''Поправка:'''<ref>Лагутин М. Б. Наглядная математическая статистика. — 345 с.</ref><ref>Кобзарь А. И. Прикладная математическая статистика. — 627 с.</ref>
+В 1978 году Р. Иман и У. Коновер предложили следующую поправку, значительно повышающую точность аппроксимации. Она использует линейную комбинацию нормальной и стьюдентовской квантилей. Положим:
+<tex>\tilde{\rho} ^{*} = \frac12 \tilde{\rho} \left[ \sqrt{n-1} + \sqrt{\frac{n-2}{1 - (\tilde{\rho})^2}} \right]</tex>.
+Гипотеза <tex>H_0</tex> отвергается в пользу альтернативы <tex>H_1\ (\rho\ >\ 0)</tex>, если <tex>\tilde{\rho} ^{*} \ge (x_{1-\alpha}+y_{1-\alpha})/2</tex>, где <tex>x_{1-\alpha},\; y_{1-\alpha}</tex> обозначают соответственно квантили уровня <tex>(1-\alpha)</tex> стандартного нормального распределения и распределения Стьюдента с <tex>n-2</tex> степенями свободы.
+==Примеры==
+Ниже приведены примеры вычисления корреляций Кенделла и Спирмена. Значения коэффициентов указаны над каждым изображением в виде <tex>(\tau,\ \rho)</tex>, где <tex>\tau</tex> - корреляция Кенделла, <tex>\rho</tex> - Спирмена. Заметно, что в большинстве случаев <tex>\left| \rho \right|\ >\ \left| \tau \right|</tex>. Объяснение этого эффекта приводится [[Коэффициент_корреляции_Кенделла#Связь коэффициентов корреляции Кенделла и Спирмена|ниже]].
+===Направление линейной зависимости===
+[[Изображение:Fig1.1-c2.png|left|frame|Корреляции Кенделла и Спирмена. Нормальные сгущения.]]<br clear="both" />
+Коэффициенты корреляции реагируют на изменение направления и зашумлённость линейной зависимости между переменными.
+===Наклон линейного тренда===
+[[Изображение:Kendall Spearman 2.png|left|frame|Корреляции Кенделла и Спирмена. Вращающаяся полоса.]]<br clear="both" />
+Коэффициенты корреляции реагируют на изменение направления, но не реагируют на изменение наклона тренда.  На первом, четвёртом и седьмом рисунках дисперсия одной из переменных близка к нулю, поэтому не удаётся зафиксировать факт линейной зависимости.
+===Нелинейная зависимость===
+[[Изображение:Kendall Spearman 3.png|left|frame|Корреляции Кенделла и Спирмена. Нелинейная зависимость.]]<br clear="both" />
+Корреляции Кенделла и Спирмена не отражают меры нелинейной зависимости между переменными.
+===Линейная и нелинейная зависимости===
+На каждой из приведённых ниже иллюстраций осуществляется переход от линейной зависимости к нелинейной. Коэффициенты корреляции Кенделла и Спирмена реагируют на это одинаковым образом.
+[[Изображение:Kendall Spearman 1.2.png|left|frame|Корреляции Кенделла и Спирмена. Перекрещенные полосы.]]<br clear="both" />
+[[Изображение:Kendall Spearman 1.3.png|left|frame|Корреляции Кенделла и Спирмена. Расширяющаяся полоса.]]<br clear="both" />
+[[Изображение:Kendall Spearman 1.4.png|left|frame|Корреляции Кенделла и Спирмена. Синусоида с переменной амплитудой.]]<br clear="both" />
+По мере смены линейной зависимости нелинейной значения коэффициентов корреляции падают.
+==Связь коэффициентов корреляции Спирмена и [[коэффициент корреляции Пирсона|Пирсона]]==
+В случае выборок из нормального распределения коэффициент корреляции Спирмена <tex>\rho</tex> может быть использован для оценки [[коэффициент корреляции Пирсона|коэффициента корреляции Пирсона]] <tex>r</tex> по формуле:
+:<tex>r=2sin{\frac{\pi}{6}\rho}</tex>.<ref>Кобзарь А. И. Прикладная математическая статистика. — 627 с.</ref>
+==Связь коэффициентов корреляции Спирмена и [[Коэффициент корреляции Кенделла|Кенделла]]==
 Выборкам <tex>x</tex> и <tex>y</tex>  соответствуют последовательности рангов:
-::<tex>R_x=(R_{x_1},\ldots,R_{x_n})</tex>, где <tex>R_{x_i}</tex> — ранг <tex>i</tex>-го объекта в [[вариационный ряд|вариационном ряду]] выборки <tex>x</tex>;
+:<tex>R_x=(R_{x_1},\ldots,R_{x_n})</tex>, где <tex>R_{x_i}</tex> — ранг <tex>i</tex>-го объекта в [[вариационный ряд|вариационном ряду]] выборки <tex>x</tex>;
-::<tex>R_y=(R_{y_1},\ldots,R_{y_n})</tex>, где <tex>R_{y_i}</tex> — ранг <tex>i</tex>-го объекта в [[вариационный ряд|вариационном ряду]] выборки <tex>y</tex>.
+:<tex>R_y=(R_{y_1},\ldots,R_{y_n})</tex>, где <tex>R_{y_i}</tex> — ранг <tex>i</tex>-го объекта в [[вариационный ряд|вариационном ряду]] выборки <tex>y</tex>.
-'''[[Коэффициент корреляции Спирмена]]''' равен
+Проведем операцию упорядочивания рангов.
-::<tex>\rho=\frac{\sum_{i=1}^n{(R_{x_i}-\frac{n+1}{2})(R_{y_i}-\frac{n+1}{2})}}{\frac{1}{12}(n^3-n)-\Delta},</tex>
-где <tex>\Delta=\frac{1}{2}\sum_{l=1}^{L_{x}}{T_{x_l}(T_{x_l}^2-1)+\frac{1}{2}\sum_{l=1}^{L_y}{T_{y_l}(T_{y_l}^2-1)}}</tex>
-==Связь коэффициента корреляции Спирмена с [[коэффициент корреляции Пирсона|коэффициентом корреляции Пирсона]]==
+Расположим ряд значений <tex>x_i</tex> в порядке возрастания величины: <tex>x_1\leq x_2\leq\cdots\leq x_n</tex>. Тогда последовательность рангов упорядоченной выборки <tex>x</tex> будет представлять собой последовательность натуральных чисел <tex>1,2,\cdots,n</tex>. Значения <tex>y</tex>, соответствующие значениям <tex>x</tex>, образуют в этом случае некоторую последовательность рангов <tex>T=(T_1,\cdots,T_n)</tex>:
-В случае выборок из нормального распределения коэффициент корреляции Спирмена <tex>\rho</tex> может быть использован для оценки [[коэффициент корреляциии Пирсона|коэффициента корреляции Пирсона]] <tex>r</tex> по формуле
+:<tex>(R_{x_i},\;R_{y_i})\rightarrow^{sort} (i,\;T_i),\; i=1,\cdots,n</tex>.
-:: <tex>r=sin{\frac{\pi\rho}{2}}</tex>
+[[Коэффициент корреляции Кенделла]] <tex>\tau</tex> и коэффициент корреляции Спирмена <tex>\rho</tex> выражаются через ранги <tex>T_i,\; i=1,\cdots,n</tex> следующим образом:
+:<tex>\rho=1-\frac{12}{n^3-n}\sum_{i<j}{(j-i)[T_i\ >\ T_j]};</tex>
+:<tex>\tau=1-\frac{4}{n^2-1}\sum_{i<j}[T_i\ >\ T_j];</tex>
+Заметно, что в случае <tex>\rho</tex> инверсиям придаются дополнительные веса <tex>(j-i)</tex>, таким образом <tex>\rho</tex> сильнее реагирует на несогласие ранжировок, чем <tex>\tau</tex>. Этот эффект проявляется в приведённых выше примерах: в большинстве из них <tex>\left| \rho \right|\ >\ \left| \tau \right|</tex>.
-== Литература ==
+'''Утверждение.'''<ref>Лагутин М. Б. Наглядная математическая статистика. — 345-346 с.</ref> Если  выборки <tex>x</tex> и <tex>y</tex> не коррелируют (выполняется гипотеза <tex>H_0</tex>), то величины <tex>\rho</tex> и <tex>\tau</tex> сильно закоррелированы. Коэффициент корреляции между ними можно вычислить по формуле:
-# ''Кобзарь А. И.'' Прикладная математическая статистика. — М.:&nbsp;Физматлит, 2006. — 816&nbsp;с.
+:<tex>corr(\rho,\;\tau)=\frac{2n+2}{\sqrt{4n^2+10n}}</tex>.
-{{UnderConstruction|[[Участник:Tsurko Varvara]] 16:00, 11 ноября 2008 (MSK)}}
+==История==
+Критерий был предложен британским психологом Чарльзом Эдвардом Спирменом в 1904 году.
+==Примечания==
+<references/>
+== Литература ==
+# ''Кобзарь А. И.'' Прикладная математическая статистика. — М.:&nbsp;Физматлит, 2006. — 626-628 с.
+# ''Лагутин М. Б.'' Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003. — 343-345 с.
+# ''Лапач С. Н., Чубенко А. В., Бабич П. Н.'' Статистика в науке и бизнесе. — Киев: Морион, 2002. — 182-184 с.
+==Ссылки==
+*[[Ранговая корреляция]]
+*[[Коэффициент корреляции Кенделла]] — другой способ расчёта ранговой корреляции.
+*[[Коэффициент корреляции Пирсона]]
+*[http://ru.wikipedia.org/wiki/Коэффициент_корреляции Коэффициент корреляции] — статья в русскоязычной Википедии.
+*[http://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient Spearman rank correlation coefficient] — статья в англоязычной Википедии.
-{{stub}}
 [[Категория:Прикладная статистика]]
 [[Категория:Энциклопедия анализа данных]]
+[[Категория:Корреляционный анализ]]
+{{Задание|Василий Ломакин|Vokov|31 декабря 2009}}