Символьная регрессия

Материал из MachineLearning.

(Различия между версиями)

Версия 19:13, 30 марта 2008

Символьная регрессия — метод построения регрессионных моделей путем перебора различных произвольных суперпозиций функций из некоторого заданного набора. Суперпозиция функций при этом называется «программой», а стохастический оптимизационный алгоритм построения таких суперпозиций называется генетическим программированием.

Генетическое программирование — модификация генетического алгоритма. Различие заключается в том, что для решения задач символьной регрессии необходима изменяющаяся длина хромосом, описывающих суперпозиции. Так как подобные алгоритмы являются переборными и требуют значительных вычислительных ресурсов, то публикации по данной теме стали появляться в 90-х годах, а значительное развитие они получили после 2000-го года. Наиболее известным исследователем является Джон Коза.

Постановка задачи

Задача отыскания оптимальной структуры регрессионной модели нескольких свободных переменных следующим образом. Задана выборка — множество $\{\mathbf{x}_1,\ldots,\mathbf{x}_N|\mathbf{x}\in\R^M\}$ значений свободных переменных и множество $\{y_1,\ldots, y_N| y\in\R\}$ соответствующих им значений зависимой переменной. Обозначим оба эти множества как множество исходных данных $D$ .

Также задано множество $G=\{g|g:\R\times\ldots\times\R\longrightarrow\R\}$ гладких параметрических функций $g=g(\mathbf{b},\cdot,\cdot,\ldots,\cdot)$ . Первый аргумент функции $g$ — вектор-строка параметров $\mathbf{b}$ , последующие — переменные из множества действительных чисел, рассматриваемые как элементы вектора свободных переменных. Рассмотрим произвольную суперпозицию, состоящую из не более чем $r$ функций $g$ . Эта суперпозиция задает параметрическую регрессионную модель $f=f(\mathbf{w},\mathbf{x})$ . Регрессионная модель $f$ зависит от вектора свободных переменных $\mathbf{x}$ и от вектора параметров $\mathbf{w}$ . Вектор $\mathbf{w}\in\R^W$ состоит из присоединенных векторов-параметров функций $g_1,\ldots, g_r$ , то есть, $\mathbf{w}=\mathbf{b}_1\vdots\mathbf{b}_2\vdots\ldots\vdots\mathbf{b}_r$ , где $\vdots$ — знак присоединения векторов. Обозначим $\Phi=\{f_i\}$ — множество всех суперпозиций, индуктивно порожденное элементами множества $G$ .

Требуется выбрать такую модель $f_i$ , которая доставляет максимум заданного функционала $p(\mathbf{w}|D)$ . Этот функционал определяет целевую функцию $S(\mathbf{w})$ , которая используется при вычислениях.

Процедура поиска оптимальной модели

Поиск оптимальной модели происходит на множестве порождаемых моделей на каждой итерации алгоритма. Перед работой алгоритма заданы множество измеряемых данных $D$ и множество гладких функций $G$ . Задан начальный набор конкурирующих моделей, $F_0=\{f_1,\ldots, f_{M}|f\in\Phi\}$ , в котором каждая модель $f_i$ есть суперпозиция функций $\{g_{ij}\}_{j=1}^{r_i}$ . Если нет начального набора моделей, то он порождается случайным образом. Далее выполняется последовательность шагов, приведенных ниже.

1. Методом сопряженных градиентов (или другим способом настройки параметров) минимизируются штрафные функции $S_i(\mathbf{w})$ для каждой модели $f_i, i=1,\ldots,M$ . Отыскиваются параметры $\mathbf{w}^\m_i$ и вычисляется значение штрафной функции каждой модели.

2. Заданы следующие правила построения производных моделей $f'_1,\ldots, f'_{M}$ . Для каждой модели $f_i$ строится производная модель $f'_i$ . В $f_i$ произвольно выбирается функция $g_{ij}$ . Выбирается произвольная модель $f_\xi$ из $F_0\backslash\{f_i\}$ и ее произвольная функция $g_{\xi\zeta}$ . Модель $f'$ порождается из модели $f$ путем замещения функции $g_{ij}$ с ее аргументами на функцию $g_{\xi\zeta}$ с ее аргументами.

3. С заданной вероятностью $\eta$ каждая модель $f'_i$ подвергается изменениям. В изменяемой модели выбирается $j$ -тая функция, причем закон распределения вероятности выбора функции $p(j)$ задан. Из множества $G$ случайным образом выбирается функция $g'$ и замещает функцию $g_j$ . Гиперпараметр $\alpha_{ij}$ этой функции определяется как $\max\limits_j(\alpha_{ij})$ . Вектор параметров этой функции $\mathbf{b}_{ij}$ равен нулю или назначается при задании $G$ .

4. При выборе моделей из объединенного множества родительских и порожденных моделей в соответствии с критерием $S(\mathbf{w})$ выбираются $M$ наилучших, которые используются в дальнейших итерациях.

Алгоритм остановливается при достижении ошибки, не превосходящей заданную, или через заданное количество раз.

Пример построения модели

Ниже описывается пример построения символьной регрессионной модели. На рис.1. сплошной кривой показаны исходные данные, пунктиром показаны значения регрессионной модели. По оси абсцисс отложено значение свободной переменной, по оси ординат — значение зависимой переменной. Выборка, представленная данной кривой, содержит четыре тысячи отсчетов. Экспертами было задано множество базовых функций $G$ из элементов которого порождаются регрессионные модели. Список функций приведен в таблице. Множество $F_0$ моделей начального приближения также было задано экспертами.

Выбор моделей производился из более тысячи порожденных моделей. В таблице 2 приведены три модели, полученные в результате работы алгоритма. Качество моделей оценивалось по ошибкам $\rho_1,\rho_2$ и числу параметров в векторе параметров $\mathbf{w}$ . Ошибка $\rho_1$ — среднеквадратичная относительная ошибка

$\rho_1=\sqrt{\frac{1}{N}\sum_{i=1}^n\left(\frac{y_i-f(\x_i)}{\max(y_i)}\right)^2},$

ошибка $\rho_2$ — максимальная относительная ошибка

$\rho_2=\max_{i=1,\ldots,N}\frac{|y_i-f(\x_i)|}{\max(y_i)}.$

В строке «Описание» таблицы 2 показана структура модели в виде дерева. В качестве примера рассмотрим модель 2. Эта модель состоит из суперпозиции восьми функций $f_2=g_1(g_2(g_3(g_4(g_5(x), g_6(x)), g_7(x)), x), g_8(x))$ . Функции $g_1=\times(\emptyset,\cdot,\cdot)$ и $g_2,\ldots, g_4=+(\emptyset,\cdot,\cdot)$ , сложения и умножения, имеют первым аргументом пустой вектор параметров; $g_5,\ldots, g_7=h(\mathbf{b}_i,\cdot)$ , $i=1,\ldots,3$ , и $g_8=l(\mathbf{b}_4,\cdot)$ . Функции $h=\frac{\lambda_i}{\sqrt{2\pi}\sigma_i}\mbox{exp}\left({-\frac{(x-\xi_i)^2}{2\sigma_i^2}}\right)$ имеют векторы параметров $\mathbf{b}_i=\langle\lambda_i,\mu_i,\sigma_i, a_i\rangle$ , и функция $l=(ax+b)$ имеет вектор параметров $\mathbf{b}_4=\langle{a, b}\rangle$ .

Модель $f_2$ можно переписать в виде $f(\mathbf{w},\x)=l(\mathbf{b}_4,x)^{-1}\times\left(x+\sum_{i=1}³h(\mathbf{b}_i, x)\right),$ где $\x=x$ и $\mathbf{w}=\mathbf{b}_1\vdots\mathbf{b}_2\vdots\mathbf{b}_3\vdots\mathbf{b}_4$ . Развернутый вид модели:

$y=(ax+b)^{-1}\left(x+\sum_{i=1}^3\frac{\lambda_i}{\sqrt{2\pi}\sigma_i}\mbox{exp}\left({-\frac{(x-\xi_i)^2}{2\sigma_i^2}}\right)+a_i\right).$

Литература

Zelinka, I., Nolle, L., Oplatkova, Z. Analytic Programming — Symbiloc Regression by Means of Arbitrfary Evolutionary Algorithms / Journal of Simulation. Vol. 6 No 9. P. 44—56.
Koza, J. R. Genetic Programming IV: Routine Human-Competitive Machine Intelligence. Springer. 2005.
Riolo, R., Soule, T., Worzel, B. (Eds.) Genetic Programming Theory and Practice V. Series: Genetic and Evolutionary Computation. Springer. 2008.
Madar, J., Janos, A., Szeifert, F. Genetic Programming for the Identification of Nonlinear Input-Output Models. citeseer.ist.psu.edu. 2005.
Hazan, A. et al. Modelling Expressive Performance: A Regression Tree Approach Based on Strongly Typed Genetic Programming / Applications of Evolutionary Computing. Springer. Vol. 3907/2006. P. 676—687.
Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection / Proceedings of 14 International Joint Conference of Artificial Intelligence. 2(12). P. 1137—1143.
Стрижов В.В. Поиск параметрической регрессионной модели в индуктивно заданном множестве. Журнал вычислительных технологий. 2007. No 1. С. 93-102. [1]

Внешние ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D0%B8%D0%BC%D0%B2%D0%BE%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F»

Категории: Регрессионный анализ | Энциклопедия анализа данных

@@ Строка 1: / Строка 1: @@
-'''Символьная регрессия''' — метод построения [[регрессионная модель|регрессионных моделей]]] путем перебора различных произвольных суперпозиций функций из некоторого заданного набора. Суперпозиция функций при этом называется "программой", а стохастический оптимизационный алгоритм построения таких суперпозиций называется [[генетическое программирование|генетическим программированием]].
+'''Символьная регрессия''' — метод построения [[регрессионная модель|регрессионных моделей]] путем перебора различных произвольных суперпозиций функций из некоторого заданного набора. Суперпозиция функций при этом называется «программой», а стохастический оптимизационный алгоритм построения таких суперпозиций называется [[генетическое программирование|генетическим программированием]].
-Генетическое программирование – модификация [[генетического алгоритма]]. Различие заключается в том, что для решения задач символьной регрессии необходима изменяющаяся длина хромосом, описывающих суперпозиции.
+Генетическое программирование — модификация [[генетического алгоритма]]. Различие заключается в том, что для решения задач символьной регрессии необходима изменяющаяся длина хромосом, описывающих суперпозиции.
+Так как подобные алгоритмы являются переборными и требуют значительных вычислительных ресурсов, то публикации по данной теме стали появляться в 90-х годах, а значительное развитие они получили после 2000-го года. Наиболее известным исследователем является [http://www.genetic-programming.com/ Джон Коза].
-Так как подобные алгоритмы являются переборными и требуют значительных вычислительных ресурсов, то публикации по данной теме стали появляться в 90-х годах, а значительное развитие они получили после 2000-го года. Наиболее известным исследователем является Джон Коза.
 == Постановка задачи ==
-Задача отыскания оптимальной структуры регрессионной модели нескольких свободных переменных следующим образом. Задана выборка&nbsp;— множество <tex>\{\mathbf{x}_1,…,\mathbf{x}_N|\mathbf{x}\in\R^M\}</tex> значений свободных переменных и множество <tex>\{y_1,…,y_N| y\in\R\}</tex> соответствующих им значений зависимой переменной. Обозначим оба эти множества как множество исходных данных&nbsp;<tex>D</tex>.
+Задача отыскания оптимальной структуры регрессионной модели нескольких свободных переменных следующим образом. Задана выборка&nbsp;— множество <tex>\{\mathbf{x}_1,\ldots,\mathbf{x}_N|\mathbf{x}\in\R^M\}</tex> значений свободных переменных и множество <tex>\{y_1,\ldots, y_N| y\in\R\}</tex> соответствующих им значений зависимой переменной. Обозначим оба эти множества как множество исходных данных&nbsp;<tex>D</tex>.
-Также задано множество <tex>G=\{g|g:\R\times…\times\R\longrightarrow\R\}</tex> гладких
+Также задано множество <tex>G=\{g|g:\R\times\ldots\times\R\longrightarrow\R\}</tex> гладких
-параметрических функций <tex>g=g(\mathbf{b},\cdot,\cdot,…,\cdot) </tex>. Первый аргумент функции&nbsp;<tex>g</tex>&nbsp;— вектор-строка параметров&nbsp;<tex>\mathbf{b}</tex>, последующие&nbsp;— переменные из множества действительных чисел, рассматриваемые как элементы вектора свободных переменных.
+параметрических функций <tex>g=g(\mathbf{b},\cdot,\cdot,\ldots,\cdot) </tex>. Первый аргумент функции&nbsp;<tex>g</tex>&nbsp;— вектор-строка параметров&nbsp;<tex>\mathbf{b}</tex>, последующие&nbsp;— переменные из множества действительных чисел, рассматриваемые как элементы вектора свободных переменных.
 Рассмотрим произвольную суперпозицию, состоящую из не более чем&nbsp;<tex>r</tex> функций&nbsp;<tex>g</tex>. Эта суперпозиция задает параметрическую регрессионную модель&nbsp;<tex>f=f(\mathbf{w},\mathbf{x}) </tex>. Регрессионная модель&nbsp;<tex>f</tex> зависит от вектора свободных переменных&nbsp;<tex>\mathbf{x}</tex> и от вектора параметров&nbsp;<tex>\mathbf{w}</tex>. Вектор&nbsp;<tex>\mathbf{w}\in\R^W</tex> состоит из присоединенных векторов-параметров
-функций&nbsp;<tex>g_1,…,g_r</tex>, то есть, <tex>\mathbf{w}=\mathbf{b}_1\vdots\mathbf{b}_2\vdots…\vdots\mathbf{b}_r</tex>, где <tex>\vdots</tex>&nbsp;— знак присоединения векторов. Обозначим&nbsp;<tex>\Phi=\{f_i\}</tex>&nbsp;— множество всех суперпозиций, индуктивно порожденное элементами множества&nbsp;<tex>G</tex>.
+функций&nbsp;<tex>g_1,\ldots, g_r</tex>, то есть, <tex>\mathbf{w}=\mathbf{b}_1\vdots\mathbf{b}_2\vdots\ldots\vdots\mathbf{b}_r</tex>, где <tex>\vdots</tex>&nbsp;— знак присоединения векторов. Обозначим&nbsp;<tex>\Phi=\{f_i\}</tex>&nbsp;— множество всех суперпозиций, индуктивно порожденное элементами множества&nbsp;<tex>G</tex>.
+Требуется выбрать такую модель&nbsp;<tex>f_i</tex>, которая доставляет максимум заданного функционала&nbsp;<tex>p(\mathbf{w}|D) </tex>. Этот функционал определяет целевую функцию <tex>S(\mathbf{w})</tex>,
+которая используется при вычислениях.
+== Процедура поиска оптимальной модели ==
+Поиск оптимальной модели происходит на множестве порождаемых моделей на каждой итерации алгоритма.
+Перед работой алгоритма заданы множество измеряемых данных&nbsp;<tex>D</tex> и множество гладких
+функций&nbsp;<tex>G</tex>.
+Задан начальный набор конкурирующих моделей, <tex>F_0=\{f_1,\ldots, f_{M}|f\in\Phi\}</tex>, в котором каждая модель&nbsp;<tex>f_i</tex>
+есть суперпозиция функций&nbsp;<tex>\{g_{ij}\}_{j=1}^{r_i}</tex>.
+Если нет начального набора моделей, то он порождается случайным образом.
+Далее выполняется последовательность шагов, приведенных ниже.
+.&nbsp;Методом сопряженных градиентов (или другим способом настройки параметров) минимизируются
+штрафные функции <tex>S_i(\mathbf{w})</tex> для каждой модели&nbsp;<tex>f_i, i=1,\ldots,M</tex>.
+Отыскиваются параметры&nbsp;<tex>\mathbf{w}^\m_i</tex> и вычисляется значение штрафной функции каждой модели.
+.&nbsp;Заданы следующие правила построения производных моделей
+<tex>f'_1,\ldots, f'_{M}</tex>. Для каждой модели&nbsp;<tex>f_i</tex> строится производная
+модель&nbsp;<tex>f'_i</tex>. В&nbsp;<tex>f_i</tex> произвольно выбирается функция&nbsp;<tex>g_{ij}</tex>. Выбирается произвольная модель&nbsp;<tex>f_\xi</tex> из
+<tex>F_0\backslash\{f_i\}</tex> и ее произвольная функция&nbsp;<tex>g_{\xi\zeta}</tex>.
+Модель&nbsp;<tex>f'</tex> порождается из модели&nbsp;<tex>f</tex> путем замещения
+функции&nbsp;<tex>g_{ij}</tex> с ее аргументами на функцию&nbsp;<tex>g_{\xi\zeta}</tex> с ее
+аргументами.
+.&nbsp;С заданной вероятностью&nbsp;<tex>\eta</tex> каждая модель&nbsp;<tex>f'_i</tex>
+подвергается изменениям. В изменяемой модели выбирается&nbsp;<tex>j</tex>-тая
+функция, причем закон распределения вероятности выбора
+функции&nbsp;<tex>p(j)</tex> задан. Из множества&nbsp;<tex>G</tex> случайным образом
+выбирается функция&nbsp;<tex>g'</tex> и замещает функцию&nbsp;<tex>g_j</tex>.
+Гиперпараметр&nbsp;<tex>\alpha_{ij}</tex> этой функции определяется как
+<tex>\max\limits_j(\alpha_{ij})</tex>. Вектор параметров этой
+функции&nbsp;<tex>\mathbf{b}_{ij}</tex> равен нулю или назначается при задании&nbsp;<tex>G</tex>.
+.&nbsp;При выборе моделей из объединенного множества родительских и
+порожденных моделей в соответствии с критерием&nbsp;<tex>S(\mathbf{w})</tex>
+выбираются&nbsp;<tex>M</tex> наилучших, которые используются в дальнейших
+итерациях.
+Алгоритм остановливается при достижении ошибки, не превосходящей заданную, или через
+заданное количество раз.
+== Пример построения модели ==
+[[Изображение:Symbolic_Regression_Fig1.png|right]]
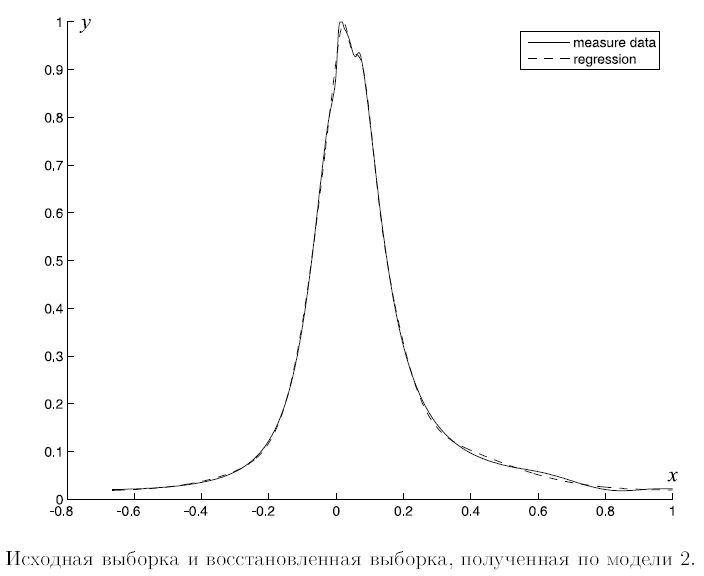
+Ниже описывается пример построения символьной регрессионной модели. На рис.1. сплошной кривой
+показаны исходные данные, пунктиром показаны значения регрессионной модели. По оси абсцисс отложено значение свободной
+переменной, по оси ординат&nbsp;— значение зависимой переменной.
+Выборка, представленная данной кривой, содержит четыре тысячи отсчетов.
+Экспертами было задано множество базовых функций&nbsp;<tex>G</tex> из элементов которого порождаются регрессионные модели.
+Список функций приведен в таблице. Множество&nbsp;<tex>F_0</tex> моделей начального приближения также было задано экспертами.
+[[Изображение:Symbolic_Regression_Table1.png]]
+Выбор моделей производился из более тысячи порожденных моделей.
+В таблице&nbsp;2 приведены три модели, полученные в результате
+работы алгоритма. Качество моделей оценивалось по ошибкам
+&nbsp;<tex>\rho_1,\rho_2</tex> и числу параметров в векторе параметров&nbsp;<tex>\mathbf{w}</tex>.
+Ошибка&nbsp;<tex>\rho_1</tex>&nbsp;— среднеквадратичная относительная ошибка
+<center><tex>\rho_1=\sqrt{\frac{1}{N}\sum_{i=1}^n\left(\frac{y_i-f(\x_i)}{\max(y_i)}\right)^2},</tex></center>
+ошибка &nbsp;<tex>\rho_2</tex>&nbsp;— максимальная относительная ошибка
+<center><tex>\rho_2=\max_{i=1,\ldots,N}\frac{|y_i-f(\x_i)|}{\max(y_i)}.</tex></center>
+[[Изображение:Symbolic_Regression_Table2.png]]
-Требуется выбрать такую модель&nbsp;<tex>f_i</tex>, которая доставляет максимум заданного функционала&nbsp;<tex>p(\mathbf{w}|D) </tex>.
+В строке «Описание» таблицы&nbsp;2 показана структура модели
+в виде дерева. В качестве примера рассмотрим модель&nbsp;2. Эта
+модель состоит из суперпозиции восьми
+функций&nbsp;<tex>f_2=g_1(g_2(g_3(g_4(g_5(x), g_6(x)), g_7(x)), x), g_8(x))</tex>.
+Функции&nbsp;<tex>g_1=\times(\emptyset,\cdot,\cdot)</tex> и
+<tex>g_2,\ldots, g_4=+(\emptyset,\cdot,\cdot)</tex>, сложения и умножения,
+имеют первым аргументом пустой вектор параметров;
+<tex>g_5,\ldots, g_7=h(\mathbf{b}_i,\cdot)</tex>, <tex>i=1,\ldots,3</tex>, и <tex>g_8=l(\mathbf{b}_4,\cdot)</tex>.
+Функции&nbsp;<tex>h=\frac{\lambda_i}{\sqrt{2\pi}\sigma_i}\mbox{exp}\left({-\frac{(x-\xi_i)^2}{2\sigma_i^2}}\right)</tex>
+имеют векторы
+параметров&nbsp;<tex>\mathbf{b}_i=\langle\lambda_i,\mu_i,\sigma_i, a_i\rangle</tex>,
+и функция&nbsp;<tex>l=(ax+b)</tex> имеет вектор
+параметров&nbsp;<tex>\mathbf{b}_4=\langle{a, b}\rangle</tex>.
-{{Заготовка}}
+Модель&nbsp;<tex>f_2</tex> можно переписать в виде
+<tex>f(\mathbf{w},\x)=l(\mathbf{b}_4,x)^{-1}\times\left(x+\sum_{i=1}³h(\mathbf{b}_i, x)\right),</tex>
+где&nbsp;<tex>\x=x</tex> и&nbsp;<tex>\mathbf{w}=\mathbf{b}_1\vdots\mathbf{b}_2\vdots\mathbf{b}_3\vdots\mathbf{b}_4</tex>.
+Развернутый вид модели:
+<center><tex>y=(ax+b)^{-1}\left(x+\sum_{i=1}^3\frac{\lambda_i}{\sqrt{2\pi}\sigma_i}\mbox{exp}\left({-\frac{(x-\xi_i)^2}{2\sigma_i^2}}\right)+a_i\right).</tex></center>
 == Литература ==
@@ Строка 26: / Строка 106: @@
 * {{s|Hazan, A. et al.}} Modelling Expressive Performance: A Regression Tree Approach Based on Strongly Typed Genetic Programming / Applications of Evolutionary Computing. Springer. Vol.&nbsp;3907/2006. P.&nbsp;676—687.
 * {{s|Kohavi, R.}} A study of cross-validation and bootstrap for accuracy estimation and model selection&nbsp;/ Proceedings of 14 International Joint Conference of Artificial Intelligence. 2(12). P. 1137—1143.
+* {{s|Стрижов В.В.}} Поиск параметрической регрессионной модели в индуктивно заданном множестве. Журнал вычислительных технологий. 2007. No 1. С. 93-102. [http://www.ccas.ru/strijov/papers/strijov07JCT.pdf]
 == Внешние ссылки ==
-* [http://alphard.ethz.ch/gerber/approx/default.html Simple Symbolic Regression Using Genetic Programming à la John Koza]
+* [http://alphard.ethz.ch/gerber/approx/default.html Simple Symbolic Regression Using Genetic Programming a` la John Koza]
 * [http://gplab.sourceforge.net {{s|Silva, S.}} GPLAB&nbsp;— A Genetic Programming Toolbox for MATLAB]
 * [http://www.staff.ncl.ac.uk/d.p.searson/gptips.htm {{s|Searson, D.}} GPTIPS&nbsp;— Genetic Programming Tool for MATLAB]
@@ Строка 35: / Строка 116: @@
 * [http://en.wikipedia.org/wiki/Genetic_programming Genetic programming, Wikipedia]
-[[Категория:Незавершенные статьи]]
 [[Категория:Регрессионный анализ]]
 [[Категория:Энциклопедия анализа данных]]

Символьная регрессия

Материал из MachineLearning.

Версия 19:13, 30 марта 2008

Содержание

Постановка задачи

Процедура поиска оптимальной модели

Пример построения модели

Литература

Внешние ссылки

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты