Логит-анализ

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м (→Простое объяснение)
 
(11 промежуточных версий не показаны.)
Строка 3: Строка 3:
Другие названия для логистической регрессии, используемые в различных прикладных областях, включают логистическую модель, Логит-модель, и классификатор максимальной энтропии.
Другие названия для логистической регрессии, используемые в различных прикладных областях, включают логистическую модель, Логит-модель, и классификатор максимальной энтропии.
-
Логистическая регрессия относится к классу моделей, известных как обобщенные линейные модели.
+
Логистическая регрессия относится к классу моделей, известных как обобщенные [[линейные модели]].
== Простое объяснение ==
== Простое объяснение ==
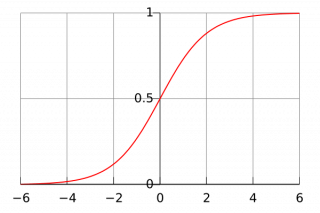
[[Image:Logistic-curve.png|thumb|320px|right|Figure 1. Логистическая функция, с z на горизонтальной оси и f (z) на вертикальной оси.]]
[[Image:Logistic-curve.png|thumb|320px|right|Figure 1. Логистическая функция, с z на горизонтальной оси и f (z) на вертикальной оси.]]
-
Объяснение логистической регрессии начинается с объяснения логистической функции:
+
Объяснение логистической регрессии начинается с объяснения [[Логистическая функция|логистической функции]]:
 +
 
:<tex>f(z)=\frac{1}{1+e^{-z}}</tex>
:<tex>f(z)=\frac{1}{1+e^{-z}}</tex>
Строка 14: Строка 15:
Типичный график логистической функции показан на рис. 1. По оси абсцисс – управляющий параметр z ("Вход"), по оси ординат f(z) - "отклик". Логистическая функция полезна, потому что она может принимать любые входные значения от минус бесконечности до плюс бесконечности, тогда как отклик (функция) ограничена диапазоном [0; 1]. Переменная z отражает подверженность некоторому набору факторов риска, в то время как f (z) представляет вероятность конкретного исхода, при заданном наборе рисков. Переменная z является мерой полного вклада всех факторов риска, используемых в модели, и известна как logit.
Типичный график логистической функции показан на рис. 1. По оси абсцисс – управляющий параметр z ("Вход"), по оси ординат f(z) - "отклик". Логистическая функция полезна, потому что она может принимать любые входные значения от минус бесконечности до плюс бесконечности, тогда как отклик (функция) ограничена диапазоном [0; 1]. Переменная z отражает подверженность некоторому набору факторов риска, в то время как f (z) представляет вероятность конкретного исхода, при заданном наборе рисков. Переменная z является мерой полного вклада всех факторов риска, используемых в модели, и известна как logit.
 +
:<tex>z=\beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + \cdots + \beta_kx_k,</tex>
:<tex>z=\beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + \cdots + \beta_kx_k,</tex>
-
где β0 называют "точкой пересечения", а <tex>\beta_1, \beta_2, \beta_3,</tex> и т. д. называют "коэффициентами регрессии" для управляющих параметров (факторов риска) <tex>x_1, x_2, x_3</tex> соответственно. Точка пересечения – фоновая величина риска, т.е. величина z, при нулевых значениях всех специфических факторов риска. Каждый из коэффициентов регрессии описывает размер вклада соответствующего фактора риска. Положительный коэффициент регрессии означает, что данный фактор увеличивает общий риск (т.е. повышает вероятность анализируемого исхода), в то время как отрицательный коэффициент означает, что этот фактор уменьшает риск; большой коэффициент регрессии означает, что данный фактор существенно влияет на совокупный риск, в то время как почти нулевой коэффициент регрессии означает, что этот фактор имеет небольшое влияние на вероятность результата.
+
где <tex>\beta_0</tex> называют "точкой пересечения", а <tex>\beta_1, \beta_2, \beta_3,</tex> и т. д. называют "коэффициентами регрессии" для управляющих параметров (факторов риска) <tex>x_1, x_2, x_3</tex> соответственно. Точка пересечения – фоновая величина риска, т.е. величина z, при нулевых значениях всех специфических факторов риска. Каждый из коэффициентов регрессии описывает размер вклада соответствующего фактора риска. Положительный коэффициент регрессии означает, что данный фактор увеличивает общий риск (т.е. повышает вероятность анализируемого исхода), в то время как отрицательный коэффициент означает, что этот фактор уменьшает риск; большой коэффициент регрессии означает, что данный фактор существенно влияет на совокупный риск, в то время как почти нулевой коэффициент регрессии означает, что этот фактор имеет небольшое влияние на вероятность результата.
Логистическая регрессия - полезный способ описать влияние одного или нескольких факторов риска (например, возраст, пол, и т.д.) на результат, такой как смерть (логистическая функция может принимать только два возможных значения: мертвый или не мертвый).
Логистическая регрессия - полезный способ описать влияние одного или нескольких факторов риска (например, возраст, пол, и т.д.) на результат, такой как смерть (логистическая функция может принимать только два возможных значения: мертвый или не мертвый).
Применимость логистической регрессии может быть продемонстрирована на фиктивном примере смертности от болезней сердца. Эта упрощенная модель использует только три фактора риска (возраст, пол, и уровень холестерина в крови), чтобы предсказать риск смерти от заболеваний сердца на десятилетний период. Вот пример подгоночной модели:
Применимость логистической регрессии может быть продемонстрирована на фиктивном примере смертности от болезней сердца. Эта упрощенная модель использует только три фактора риска (возраст, пол, и уровень холестерина в крови), чтобы предсказать риск смерти от заболеваний сердца на десятилетний период. Вот пример подгоночной модели:
 +
:<tex>\beta_0=-5.0 </tex> пересечение
:<tex>\beta_0=-5.0 </tex> пересечение
Строка 33: Строка 36:
Согласно этой модели, вероятность смерти в результате болезни сердца определяется формулой:
Согласно этой модели, вероятность смерти в результате болезни сердца определяется формулой:
-
:<tex>\text{risk of death} = \frac{1}{1+e^{-z}} \text{, where } z=-5.0 +2.0x_1 -1.0x_2 + 1.2x_3.</tex>
+
 
 +
:<tex>\text{risk of death} = \frac{1}{1+e^{-z}}</tex> где <tex>z=-5.0 +2.0x_1 -1.0x_2 + 1.2x_3.</tex>
Строка 43: Строка 47:
-
: <tex> \frac{1}{1+e^{-z}} \text{, where } z=-5.0 + (+2.0)(5.0-5.0) + (-1.0)0 + (+1.2)(7.0-5.0).</tex>
+
: <tex> \frac{1}{1+e^{-z}} </tex> где <tex> z=-5.0 + (+2.0)(5.0-5.0) + (-1.0)0 + (+1.2)(7.0-5.0).</tex>
Строка 50: Строка 54:
==Формальное математическое описание==
==Формальное математическое описание==
-
Логистическая регрессия анализирует биномиально распределенные данные вида
+
Логистическая регрессия анализирует [[биномиально]] распределенные данные вида
 +
 
:<tex>Y_i \ \sim B(n_i,p_i),\text{ for }i = 1, \dots , m,</tex>
:<tex>Y_i \ \sim B(n_i,p_i),\text{ for }i = 1, \dots , m,</tex>
Строка 58: Строка 63:
Модель предлагает для каждого испытания (значения i) ряд объяснительных переменных, которые могли бы предсказать итоговую вероятность всхода. Влияющие переменные можно рассматривать как k-мерный вектор и модель тогда принимает вид:
Модель предлагает для каждого испытания (значения i) ряд объяснительных переменных, которые могли бы предсказать итоговую вероятность всхода. Влияющие переменные можно рассматривать как k-мерный вектор и модель тогда принимает вид:
 +
:<tex>p_i = \operatorname{E}\left(\left.\frac{Y_i}{n_{i}}\right|X_i \right). \,\!</tex>
:<tex>p_i = \operatorname{E}\left(\left.\frac{Y_i}{n_{i}}\right|X_i \right). \,\!</tex>
Строка 63: Строка 69:
Логиты неизвестных биномиальных вероятностей (то есть, логарифмы перевесов, p/(1-p)) моделируются линейной функцией Xi:
Логиты неизвестных биномиальных вероятностей (то есть, логарифмы перевесов, p/(1-p)) моделируются линейной функцией Xi:
 +
:<tex>\operatorname{logit}(p_i)=\ln\left(\frac{p_i}{1-p_i}\right) = \beta_0 + \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i}.</tex>
:<tex>\operatorname{logit}(p_i)=\ln\left(\frac{p_i}{1-p_i}\right) = \beta_0 + \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i}.</tex>
-
Заметим, что некий элемент Xi может быть установлен в 1 для всех i, чтобы задать точку пересечения в модели. Неизвестные параметры βj обычно оцениваются методом максимального правдоподобия.
+
Заметим, что некий элемент Xi может быть установлен в 1 для всех i, чтобы задать точку пересечения в модели. Неизвестные параметры βj обычно оцениваются [[методом максимального правдоподобия]].
Интерпретация оценок параметров βj может быть представлена как совокупный эффект перемножения перевесов (сложения – в логарифмическом представлении) для изменения вероятности на порядок за счет j-ой влияющей переменной. В случае дихотомической объяснительной переменной (например пол), экспонента β является оценкой перевеса полов в итоговой вероятности, скажем, смертности мужчин по сравнению с женщинами.
Интерпретация оценок параметров βj может быть представлена как совокупный эффект перемножения перевесов (сложения – в логарифмическом представлении) для изменения вероятности на порядок за счет j-ой влияющей переменной. В случае дихотомической объяснительной переменной (например пол), экспонента β является оценкой перевеса полов в итоговой вероятности, скажем, смертности мужчин по сравнению с женщинами.
У модели есть эквивалентная формулировка
У модели есть эквивалентная формулировка
 +
:<tex>p_i = \frac{1}{1+e^{-(\beta_0 + \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i})}}. \,\!</tex>
:<tex>p_i = \frac{1}{1+e^{-(\beta_0 + \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i})}}. \,\!</tex>
 +
 +
 +
Эту функциональную форму обычно называют однослойным [[персептрон|персептроном]], или искусственной [[нейронная сеть|нейронной сетью]]. Однослойная нейронная сеть вычисляет непрерывный отклик функции вместо пошагового вычисления. Производная pi по X = x1... xk вычисляется согласно общей формуле:
 +
 +
 +
: <tex>y = \frac{1}{1+e^{-f(X)}}</tex>
 +
 +
 +
где f (X) является аналитической функцией от X. С этим выбором, однослойная нейронная сеть идентична логистической регрессионной модели. У этой функции есть непрерывная производная, которая позволяет этому использоваться в обратной связи. Эта функция также предпочтительна, потому что ее производная легко вычисляется:
 +
 +
 +
: <tex>y' = y(1-y)\frac{\mathrm{d}f}{\mathrm{d}X}\,\!</tex>
 +
 +
 +
== See also ==
 +
* [[Логистическая функция]]
 +
* [[Функция Логит]]
 +
* [[Sigmoid function]]
 +
 +
 +
 +
==ССылки==
 +
* [http://statpages.org/logistic.html Web-калькулятор логистической регрессии]
 +
* [http://www.cs.utah.edu/~hal/megam оптимизированный пакет моделирования максимальной энтропии ]
 +
* [http://mallet.cs.umass.edu/ MALLET Java библиотека, включает набор для логистических моделей]
 +
 +
 +
==Литература==
 +
* Agresti, Alan. (2002). Categorical Data Analysis. New York: Wiley-Interscience. ISBN 0-471-36093-7.
 +
* Amemiya, T. (1985). Advanced Econometrics. Harvard University Press. ISBN 0-674-00560-0.
 +
* Balakrishnan, N. (1991). Handbook of the Logistic Distribution. Marcel Dekker, Inc.. ISBN 978-0824785871.
 +
* Greene, William H. (2003). Econometric Analysis, fifth edition. Prentice Hall. ISBN 0-13-066189-9.
 +
* Hosmer, David W.; Stanley Lemeshow (2000). Applied Logistic Regression, 2nd ed.. New York; Chichester, Wiley. ISBN 0-471-35632-8.
 +
 +
[[Категория:Регрессионный анализ]]

Текущая версия

В статистике логистическая регрессия - модель, используемая для предсказания вероятности возникновения события «подгоном» данных к логистической кривой. При этом используют несколько предсказывающих переменных, которые могут быть или числовыми или категориальными. Например, вероятность, того, что у человека случится сердечный приступ в определенный период времени, может быть предсказана в зависимости от возраста человека, пола и индекса массы тела. Логистическая регрессия широко используется в медицинских и общественных науках, так же в маркетинговых исследованиях, таких как предсказание склонности клиента купить определенный продукт или прекратить подписку.

Другие названия для логистической регрессии, используемые в различных прикладных областях, включают логистическую модель, Логит-модель, и классификатор максимальной энтропии.

Логистическая регрессия относится к классу моделей, известных как обобщенные линейные модели.


Содержание

Простое объяснение

Figure 1. Логистическая функция, с z на горизонтальной оси и f (z) на вертикальной оси.
Figure 1. Логистическая функция, с z на горизонтальной оси и f (z) на вертикальной оси.

Объяснение логистической регрессии начинается с объяснения логистической функции:


f(z)=\frac{1}{1+e^{-z}}


Типичный график логистической функции показан на рис. 1. По оси абсцисс – управляющий параметр z ("Вход"), по оси ординат f(z) - "отклик". Логистическая функция полезна, потому что она может принимать любые входные значения от минус бесконечности до плюс бесконечности, тогда как отклик (функция) ограничена диапазоном [0; 1]. Переменная z отражает подверженность некоторому набору факторов риска, в то время как f (z) представляет вероятность конкретного исхода, при заданном наборе рисков. Переменная z является мерой полного вклада всех факторов риска, используемых в модели, и известна как logit.


z=\beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + \cdots + \beta_kx_k,


где \beta_0 называют "точкой пересечения", а \beta_1, \beta_2, \beta_3, и т. д. называют "коэффициентами регрессии" для управляющих параметров (факторов риска) x_1, x_2, x_3 соответственно. Точка пересечения – фоновая величина риска, т.е. величина z, при нулевых значениях всех специфических факторов риска. Каждый из коэффициентов регрессии описывает размер вклада соответствующего фактора риска. Положительный коэффициент регрессии означает, что данный фактор увеличивает общий риск (т.е. повышает вероятность анализируемого исхода), в то время как отрицательный коэффициент означает, что этот фактор уменьшает риск; большой коэффициент регрессии означает, что данный фактор существенно влияет на совокупный риск, в то время как почти нулевой коэффициент регрессии означает, что этот фактор имеет небольшое влияние на вероятность результата. Логистическая регрессия - полезный способ описать влияние одного или нескольких факторов риска (например, возраст, пол, и т.д.) на результат, такой как смерть (логистическая функция может принимать только два возможных значения: мертвый или не мертвый). Применимость логистической регрессии может быть продемонстрирована на фиктивном примере смертности от болезней сердца. Эта упрощенная модель использует только три фактора риска (возраст, пол, и уровень холестерина в крови), чтобы предсказать риск смерти от заболеваний сердца на десятилетний период. Вот пример подгоночной модели:


\beta_0=-5.0 пересечение
\beta_1=+2.0
\beta_2=-1.0
\beta_3=+1.2
x_1= возраст, превышение пятидесятилетия в десятках лет;
x_2= пол, может принимать значения 0 (муж.) или 1 (жен.)
x_3= уровень холестерина в моль/л, уменьшенный на 5,0


Согласно этой модели, вероятность смерти в результате болезни сердца определяется формулой:


\text{risk of death} = \frac{1}{1+e^{-z}} где z=-5.0 +2.0x_1 -1.0x_2 + 1.2x_3.


зависящей от возраста, пола и уровня холестерина.

В этой модели, увеличение возраста приводит к увеличению риска смерти от болезни сердца (z повышается на 2.0 в течение каждых 10 лет в возрасте старше 50), женщины менее подвержены сердечным заболеваниям, чем мужчины (z понижается 1.0, если пациентка - женщина), и превышение содержания холестерина над пороговым уровнем приводит к увеличению риска смерти (z повышается на 1.2 для каждого 1 ммоль/л холестерина свыше 5ммоль/л).

Применим эту модель для оценки риск смерти некоего Петренко Ивана Карловича: ему 50 лет, и его уровень холестерина - 7.0 mmol/L.


\frac{1}{1+e^{-z}} где z=-5.0 + (+2.0)(5.0-5.0) + (-1.0)0 + (+1.2)(7.0-5.0).


Согласно модели, риск смерти господина Петренко от болезни сердца за следующие 10 лет составляет 0.07 (или 7 %).

Формальное математическое описание

Логистическая регрессия анализирует биномиально распределенные данные вида


Y_i \ \sim B(n_i,p_i),\text{ for }i = 1, \dots , m,


где числа Бернуллиевых испытаний ni известны, а вероятности успеха pi неизвестны. Пример этого распределения - доля семян i-го сорта, которые прорастают после того, как ni посеяны.

Модель предлагает для каждого испытания (значения i) ряд объяснительных переменных, которые могли бы предсказать итоговую вероятность всхода. Влияющие переменные можно рассматривать как k-мерный вектор и модель тогда принимает вид:


p_i = \operatorname{E}\left(\left.\frac{Y_i}{n_{i}}\right|X_i \right). \,\!


Логиты неизвестных биномиальных вероятностей (то есть, логарифмы перевесов, p/(1-p)) моделируются линейной функцией Xi:


\operatorname{logit}(p_i)=\ln\left(\frac{p_i}{1-p_i}\right) = \beta_0 + \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i}.


Заметим, что некий элемент Xi может быть установлен в 1 для всех i, чтобы задать точку пересечения в модели. Неизвестные параметры βj обычно оцениваются методом максимального правдоподобия.

Интерпретация оценок параметров βj может быть представлена как совокупный эффект перемножения перевесов (сложения – в логарифмическом представлении) для изменения вероятности на порядок за счет j-ой влияющей переменной. В случае дихотомической объяснительной переменной (например пол), экспонента β является оценкой перевеса полов в итоговой вероятности, скажем, смертности мужчин по сравнению с женщинами.

У модели есть эквивалентная формулировка


p_i = \frac{1}{1+e^{-(\beta_0 + \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i})}}. \,\!


Эту функциональную форму обычно называют однослойным персептроном, или искусственной нейронной сетью. Однослойная нейронная сеть вычисляет непрерывный отклик функции вместо пошагового вычисления. Производная pi по X = x1... xk вычисляется согласно общей формуле:


y = \frac{1}{1+e^{-f(X)}}


где f (X) является аналитической функцией от X. С этим выбором, однослойная нейронная сеть идентична логистической регрессионной модели. У этой функции есть непрерывная производная, которая позволяет этому использоваться в обратной связи. Эта функция также предпочтительна, потому что ее производная легко вычисляется:


y' = y(1-y)\frac{\mathrm{d}f}{\mathrm{d}X}\,\!


See also


ССылки


Литература

  • Agresti, Alan. (2002). Categorical Data Analysis. New York: Wiley-Interscience. ISBN 0-471-36093-7.
  • Amemiya, T. (1985). Advanced Econometrics. Harvard University Press. ISBN 0-674-00560-0.
  • Balakrishnan, N. (1991). Handbook of the Logistic Distribution. Marcel Dekker, Inc.. ISBN 978-0824785871.
  • Greene, William H. (2003). Econometric Analysis, fifth edition. Prentice Hall. ISBN 0-13-066189-9.
  • Hosmer, David W.; Stanley Lemeshow (2000). Applied Logistic Regression, 2nd ed.. New York; Chichester, Wiley. ISBN 0-471-35632-8.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9B%D0%BE%D0%B3%D0%B8%D1%82-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7»
Личные инструменты