Непараметрическая регрессия: ядерное сглаживание

Материал из MachineLearning.

(Различия между версиями)

Перейти к: навигация, поиск

Текущая версия

Ядерное сглаживание - один из простейших видов непараметрической регрессии.

Содержание

1 Постановка задачи
2 Принцип
3 Описание метода
4 Литература
5 См. также

Постановка задачи

Решается задача восстановления регрессии. Задано пространство объектов $X$ и множество возможных

ответов $Y=R$ . Существует неизвестная целевая зависимость $y^*: X \rightarrow Y$ , значения которой известны только на объектах обучающей выборки $X^m={(x_i, y_i)}_{i=1}^m$ . Требуется построить алгоритм $a: X \rightarrow Y$ , аппроксимирующий целевую зависимость $y^*$ .

Принцип

Принцип, используйщий идейно простой подход к представлению последовательности весов $\{ W_{mi}(x) \}_{i=1}^m$ состоит в описании формы весовой функции $W_{mi}(x)$ посредством функции плотности со скалярным параметром, который регулирует размер и форму весов около х. Эту функцию формы принято называть ядром $K$ .

Полученные таким образом веса далее используются для представления величины $a(x)$ в виде взвешенной суммы значений $y_i$ обучающей выборки.

Описание метода

Определение ядра

Ядро — это непрерывная ограниченная симметричная вещественная функция $K$ с единичным интегралом

$\int K(u)du=1$

Последовательность весов

Последовательность весов для ядерных оценок (для одномерного $x$ ) определяется как :: $W_{mi}(x)=\frac{K_{h_m}(x-X_i)}{\hat{f}_{h_m}(x)}$ , где

$\hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x-X_i)$ ,

$K_{h_m}(u)=\frac{1}{h_m} K$\frac{u}{h_m}$$

представляет собой ядро с параметром $h_m$ . Этот параметр принято называть шириной окна. Подчеркнув зависимость $h\ =\ h_m$ от объема выборки $m$ , условимся сокращенно обозначать последовательность весов $W_{mi}(x)$ .

Функция ядра

Функция $\hat{f}_{h_m}(x)$ является ядерной оценкой плотности Розенблата — Парзена (Rosenblatt, 1956; Parzen, 1962) для (маргинальной) плотности переменной $x$ . Данный вид ядерных весов $W_{mi}(x)$ был предложен в работах (Nadaraya, 1964) и (Watson, 1964). Как следствие, оценка ожидаемой величины восстанавливаемой зависимости $E(y\|x)$ :

$\hat{m}_h(x)=\frac{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-X_i)Y_i}{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-X_i)}$

часто называют оценкой Надарая—Ватсона. Ширина окна определяет, насколько быстро убывают веса $W_{mi}(x)$ по мере удаления объектов $x_i$ от $x$ . Характер убывания определяется видом ядра $K$ . Нормализация весов $\hat{f}_{h_m}(x)$ гарантирует, что сумма весов равна единице.

Замечание. При ряде условий имеет место сходимость по вероятности данной оценки к $E(y|x)$ .

Пример функции ядра

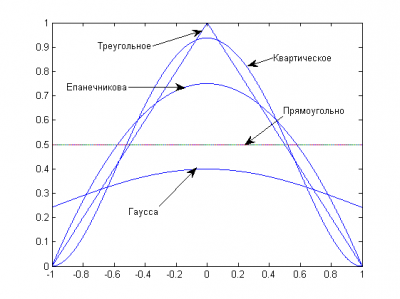
Примеры различных функций ядра.

На практике используется несколько видов ядерных функций. Чаще всего используется квартическая ядерная функция

$K(u)=(15/16)(1-u^2)^2I(\| u \| \le 1)$ .

Также используется ядро Епанечникова, обладающее некоторыми свойствами оптимальности [Хардле В п4.5]; это функция параболического типа (Epanechnikov, 1969; Bartlett, 1963):

$K(u)=0.75(1-u^2)I(\| u \| \le 1)$ .

Другими примерами являются ядро Гаусса,

$K(u)=(2\pi)^{-1/2} \exp(-u^2/2)$ ,

треугольное ядро

$K(u)=(1-\|u\|)I(\| u \| \le 1)$ ,

и прямоугольное ядро

$K(u)=(1/2)I(\| u \| \le 1)$ .

Замечание. Точность восстанавливаемой зависимости мало зависит от выбора ядра. Ядро определяет степень гладкости функции $a(x)$ .

Зависимость от ширины окна

Выбор окна решающим образом влияет на точность восстанавливаемой зависимости. При чересчур малых значениях $h$ кривая $a(x)$ стремится пройти через каждую точку выборки, остро реагируя на шумы и претерпевая резкие скачки, поскольку в этом случае оценка опирается только на небольшое число наблюдений из узкой окрестности точки $x$ . Наоборот, если ширина окна велика, функция чрезмерно сглаживается и в пределе при $h \rightarrow \infty$ вырождается в константу -- усреднённое значение величин $y_i$ . В этом случае сглаженная функция не даёт возможности определить характерные особенности искомой зависимости $y^*(x)$ .

Литература

Хардле В. Прикладная непараметрическая регрессия. — 1989.
Воронцов К.В. Лекции по алгоритмам восстановления регрессии. — 2007.
Лагутин М.Б. Наглядная математическая статистика. — 2009.

См. также

Данная статья была создана в рамках учебного задания.

Студент: Участник:Tolstikhin

Преподаватель: Участник:Vokov

Срок: 31 декабря 2009

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9D%D0%B5%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F:_%D1%8F%D0%B4%D0%B5%D1%80%D0%BD%D0%BE%D0%B5_%D1%81%D0%B3%D0%BB%D0%B0%D0%B6%D0%B8%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5»

Категория: Непараметрическая регрессия

@@ Строка 20: / Строка 20: @@
 ::<tex>\int K(u)du=1</tex>
 === Последовательность весов ===
-Последовательность весов для ядерных оценок (для одномерного <tex>x</tex>) определяется как ::<tex>W_{mi}(x)=\frac{K_{h_m}(x\;-\;X_i)}{\hat{f}_{h_m}(x)}</tex>,
+Последовательность весов для ядерных оценок (для одномерного <tex>x</tex>) определяется как ::<tex>W_{mi}(x)=\frac{K_{h_m}(x-X_i)}{\hat{f}_{h_m}(x)}</tex>,
 где
-::<tex>\hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x\;-\;X_i)</tex>,
+::<tex>\hat{f}_{h_m}(x)=\frac1m \sum_{i=1}^m K_{h_m}(x-X_i)</tex>,
 a
 ::<tex>K_{h_m}(u)=\frac{1}{h_m} K\(\frac{u}{h_m}\)</tex>
@@ Строка 31: / Строка 31: @@
 переменной <tex>x</tex>. Данный вид ядерных весов <tex>W_{mi}(x)</tex> был предложен в работах (Nadaraya, 1964) и (Watson, 1964). Как следствие, оценка
 ожидаемой величины восстанавливаемой зависимости <tex>E(y\|x)</tex>:
-::<tex>\hat{m}_h(x)=\frac{m^{-1}\sum_{i=1}^m K_{h_m}(x\;-\;X_i)Y_i}{m^{-1}\sum_{i=1}^m K_{h_m}(x\;-\;X_i)}</tex>
+::<tex>\hat{m}_h(x)=\frac{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-X_i)Y_i}{\frac1m\textstyle\sum\limits_{i=1}^m K_{h_m}(x-X_i)}</tex>
-часто называют оценкой ''Надарая — Ватсона''.
+часто называют оценкой ''Надарая—Ватсона''.
-Ширина окна определяет насколько быстро убывают веса <tex>W_{mi}(x)</tex> по мере удаления объектов <tex>x_i</tex> от <tex>x</tex>.
+Ширина окна определяет, насколько быстро убывают веса <tex>W_{mi}(x)</tex> по мере удаления объектов <tex>x_i</tex> от <tex>x</tex>.
 Характер убывания определяется видом ядра <tex>K</tex>.
 Нормализация весов <tex>\hat{f}_{h_m}(x)</tex> гарантирует, что сумма весов равна единице.
 '''Замечание'''. При ряде условий имеет место сходимость по вероятности данной оценки к <tex>E(y|x)</tex>.
 === Пример функции ядра ===
 [[Изображение:CoreFunc.png|thumb|right|400px|Примеры различных функций ядра.]]
@@ Строка 85: / Строка 86: @@
 }}
 ==См. также==
-* [[Ядерное сглаживание]]
 * [[Алгоритм LOWESS]]
 * [[Вариация и смещение]]
 * [[Регрессионный анализ]]
-[[Категория:Регрессионный анализ]]
+[[Категория:Непараметрическая регрессия]]
 {{ЗаданиеВыполнено|Tolstikhin|Vokov|31 декабря 2009}}