Функция конкурентного сходства

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м (Небольшая правка)
 
(11 промежуточных версий не показаны.)
Строка 1: Строка 1:
-
{{Задание|osa|Константин Воронцов|25 января 2010}}
+
'''Функция конкурентного сходства''' или '''FRiS-функция''' – мера [[сходство|сходства]] двух объектов, исчисляемая относительно некоторого иного объекта.
 +
== Введение ==
-
'''Функция конкурентного сходства''' или '''FRiS-функция''' – мера [[сходство|сходства]] двух объектов, исчисляемая относительно некоторого иного объекта.
+
FRiS-функция, в отличие от других существующих мер [[сходство|сходства]] позволяет не просто отвечать на вопросы вида «далеко-близко?», «похож-не похож?», но также давать количественную оценку ответа на вопрос «по сравнению с чем?». Такой подход позволяет учитывать большее число факторов при классификации.
== Основная формула ==
== Основная формула ==
-
Пусть имеется некоторое пространство объектов <tex>X</tex> с заданной метрикой <tex>\rho(x,x^{\prime})</tex>. Тогда [[сходство]] объектов <tex>x \in X</tex> и <tex>u \in X</tex> в конкуренции с <tex>x^{\prime} \in X</tex> исчисляется по следующей формуле:
+
Пусть имеется некоторое пространство объектов <tex>X</tex> с заданной [[метрика|метрикой]] <tex>\rho(x,x^{\prime})</tex>. Тогда '''FRiS-функция для объектов <tex>x \in X</tex> и <tex>u \in X</tex> относительно <tex>x^{\prime} \in X</tex>''' исчисляется по следующей формуле:
-
<tex>S(u,x | x^{\prime}) = \frac{\rho(u,x^{\prime}) - \rho(u,x)}{\rho(u,x^{\prime}) + \rho(u,x)}</tex>.
+
<tex>S(u,x | x^{\prime}) = \frac{\rho(u,x^{\prime}) - \rho(u,x)}{\rho(u,x^{\prime}) + \rho(u,x)}</tex>
 +
 
 +
Эту функция также называется '''сходством объектов <tex>x \in X</tex> и <tex>u \in X</tex> в конкуренции с <tex>x^{\prime} \in X</tex>'''.
== Свойства ==
== Свойства ==
Строка 14: Строка 17:
FRiS-функция обладает следующими свойствами:
FRiS-функция обладает следующими свойствами:
-
1. Область значений: <tex>E(S(u,x | x^{\prime})) = [-1,1]</tex> <br />
+
1. Область значений функции <tex>S(u,x | x^{\prime})</tex> составляет отрезок <tex>[-1,1]</tex><br />
-
2. <tex>S(u,x | x^{\prime})</tex> возрастает, если <tex>u</tex> приближается к <tex>x</tex> <br />
+
2. Функция <tex>S(u,x | x^{\prime})</tex> возрастает, если <tex>u</tex> приближается к <tex>x</tex> <br />
3. <tex>S(u,u | x^{\prime}) = 1</tex>, <tex>S(u,x | u) = -1</tex> <br />
3. <tex>S(u,u | x^{\prime}) = 1</tex>, <tex>S(u,x | u) = -1</tex> <br />
-
4. Если <tex>\rho(u,x)=\rho(u,x^{\prime})</tex>, то <tex>S(u,x|x^{\prime})</tex> <br />
+
4. Если <tex>\rho(u,x)=\rho(u,x^{\prime})</tex>, то <tex>S(u,x|x^{\prime}) = 0</tex> <br />
5. <tex>S(u,x | x^{\prime}) = S(x,u | x^{\prime}) \not= S(u,x^{\prime} | x)</tex>
5. <tex>S(u,x | x^{\prime}) = S(x,u | x^{\prime}) \not= S(u,x^{\prime} | x)</tex>
 +
 +
== Пример ==
 +
 +
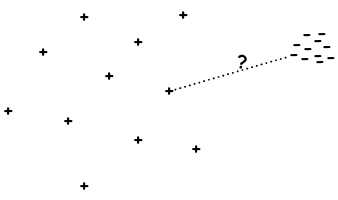
На рисунке ниже приведён пример случая, когда FRiS функция, как мера сходства, работает лучше,
 +
чем обычная [[метрика]]:
 +
[[Изображение:FRiS.jpg|thumbs]] <br />
 +
Здесь имеются объекты двух классов: «+» и «-». Классифицируемый объект «?» лежит ближе к классу «-», однако, судя по структуре классов, он является более типичным представителем класса «+» и должен быть отнесён именно в этот класс. <br />
 +
FRiS-функция в большинстве подобных случаев работает корректно.
 +
 +
== См. также ==
 +
 +
* [[Алгоритм FRiS-СТОЛП]]
 +
 +
* [http://www.springerlink.com/content/011w0802166238l4/fulltext.pdf N. G. Zagoruiko, I. A. Borisova, V. V. Dyubanov and O. A. Kutnenko. «Methods of recognition based on the function of rival similarity»]
 +
 +
 +
 +
{{Задание|osa|Константин Воронцов|21 января 2010}}
 +
 +
[[Категория:Метрические алгоритмы классификации]]

Текущая версия

Функция конкурентного сходства или FRiS-функция – мера сходства двух объектов, исчисляемая относительно некоторого иного объекта.

Содержание

Введение

FRiS-функция, в отличие от других существующих мер сходства позволяет не просто отвечать на вопросы вида «далеко-близко?», «похож-не похож?», но также давать количественную оценку ответа на вопрос «по сравнению с чем?». Такой подход позволяет учитывать большее число факторов при классификации.

Основная формула

Пусть имеется некоторое пространство объектов X с заданной метрикой \rho(x,x^{\prime}). Тогда FRiS-функция для объектов x \in X и u \in X относительно x^{\prime} \in X исчисляется по следующей формуле: 

  S(u,x | x^{\prime}) = \frac{\rho(u,x^{\prime}) - \rho(u,x)}{\rho(u,x^{\prime}) + \rho(u,x)}

Эту функция также называется сходством объектов x \in X и u \in X в конкуренции с x^{\prime} \in X.

Свойства

FRiS-функция обладает следующими свойствами:

1. Область значений функции S(u,x | x^{\prime}) составляет отрезок [-1,1]
2. Функция S(u,x | x^{\prime}) возрастает, если u приближается к x
3. S(u,u | x^{\prime}) = 1, S(u,x | u) = -1
4. Если \rho(u,x)=\rho(u,x^{\prime}), то S(u,x|x^{\prime}) = 0
5. S(u,x | x^{\prime}) = S(x,u | x^{\prime}) \not= S(u,x^{\prime} | x)

Пример

На рисунке ниже приведён пример случая, когда FRiS функция, как мера сходства, работает лучше, чем обычная метрика: 

thumbs

Здесь имеются объекты двух классов: «+» и «-». Классифицируемый объект «?» лежит ближе к классу «-», однако, судя по структуре классов, он является более типичным представителем класса «+» и должен быть отнесён именно в этот класс.
FRiS-функция в большинстве подобных случаев работает корректно.

См. также



Данная статья является непроверенным учебным заданием.
Студент: Участник:osa
Преподаватель: Участник:Константин Воронцов
Срок: 21 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%BA%D0%BE%D0%BD%D0%BA%D1%83%D1%80%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D0%B3%D0%BE_%D1%81%D1%85%D0%BE%D0%B4%D1%81%D1%82%D0%B2%D0%B0»