Прореживание двухслойной нейронной сети (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 15:30, 21 апреля 2010

Прореживание двухслойной нейронной сети (optimal brain damage) — метод упрощения структуры нейронной сети. Идея прореживания состоит в том, что из сети удаляются параметры, оказывающие малое влияние на ошибку аппроксимации. Таким образом, модель упрощается, а ошибка аппроксимации возрастает незначительно.

Содержание

1 Постановка задачи
2 Настройка нейронной сети
3 Алгоритм оптимального прореживания
4 Примеры на модельных данных
- 4.1 Пример 1: выборка линейно разделима
- 4.2 Пример 2: выборка линейно неразделима
5 Исходный код
6 См. также
7 Литература

Постановка задачи

Задана обучающая выборка $X^l, Y^l$ . Требуется решить задачу классификации с использованием двухслойной нейронной сети; затем упростить сеть, выбросив из нее параметры, соответствующие наименьшей степени выпуклости; среднеквадратичная ошибка классификации при этом не должна сильно возрасти.

Настройка нейронной сети

Двухслойная нейронная сеть состоит из одного скрытого слоя и выходного слоя. Каждый нейрон сети имеет сигмоидальную функции активации $\phi(z) = 1 / (1 + e^{-z})$ . Значения признаков $x^i$ поступают на вход первому (скрытому) слою сети с весовой матрицей $W$ , выходы первого слоя поступают на вход второму с весовой матрицей $K$ .На выходе второго слоя вычисляется вектор-функция $\bf{F} = (F_1(x),...,F_P(x))$ , где $P$ - количество нейронов на втором слое. Необходимо настроить параметры сети, используя алгоритм обратного распространения (back propagation). $\bf{E}(\bf{w}) = \frac{1}{2N} \sum_{n = 1}^N \sum_{p = 1}^P(F_p(n) - Y_p(n))^2$ - нормированная среднеквадратичная ошибка. Пусть $w_{ji}$ - вес, соединяющий нейрон $i$ с нейроном $j$ следующего слоя. Тогда коррекция веса, применяемая к $w_{ji}(n)$ , определяется согласно правилу $\Delta w_{ji} = \eta \bf{\delta}_j(n)y_i(n)$ , где $\bf{\delta}_j(n) = - \frac{\partial \bf{E}(n)}{\partial y_j(n)}\phi_j'(v_j(n))$ - локальный градиент нейрона j. Здесь $y_i(n)$ - выход i-го нейрона, $v_j(n) = \sum_{i = 1}^m w_{ji}(n)y_i(n)$ - значение, которое получает на вход функция активации, соответствующая j-му нейрону (m - количество его входов), $\eta$ - темп обучения. Поскольку ошибка представляется в виде $\bf{E}(n) = \frac{1}{2}\sum_{p = 1}^P (F_p(n) - y_p(n))^2$ , то для выходного слоя $\frac {\partial \bf{E}(n)}{\partial y_j(n)} = y_j(n) - F_j(n) =: e_j(n)$ , и для него справедливо $\Delta w_{ji} = - \eta e_j(n)\phi_j'(v_j(n))y_i(n)$ . Соответственно, для первого, скрытого, слоя справедлива формула обратного распространения $\delta_j(n) = \phi_j'(v_j(n)) \sum_{p = 1}^P \delta_p(n) w_{pj}(n)$ .

Алгоритм оптимального прореживания

Описание метода второго порядка приводится в статье Оптимальное прореживание нейронных сетей.

Основное отличие данного метода состоит в допущении, что матрица Гессе является диагональной. Таким образом, алгоритм немного видоизменяется:

Задана выборка $X$ , модель $f(w)$ , функция ошибки $E_X$ . Для упрощения структуры сети выполняем следующие шаги:
1. настраиваем модель, получаем параметры $\bf{w}$ .
2. пока значение ошибки не превосходит заранее заданного (3-5):
3. вычисляем гессиан $H$ согласно формуле
$H_{jk} = \frac{1}{N}\sum_{n = 1}^N \sum_{p = 1}^P ((\frac{\partial F_p}{\partial w_{kj}})^2 - \frac{\partial^2 F_p}{\partial w_{kj}^2}(F_p(n) - y_p(n)))$
обозначим за $U_j^{(l)}$ аргумент функции активации нейрона $j$ на слое $l$ . Тогда частные производные на втором слое:
$\frac{\partial F_p}{\partial w_{kj}} = \phi'(U_k^{(2)}) \phi (U_j^{(1)});$
$\frac{\partial^2 F_p}{\partial w_{kj}^2} = \phi''(U_k^{(2)}) \phi^2 (U_j^{(1)})$ при $p$ = $k$ и равны 0 при $p \neq k$ ,
а на первом слое
$\frac{\partial F_p}{\partial w_{ji}} = \phi'(U_p^{(2)})w_{pj}\phi'(U_j^{(1)})x_iw_{ij}$ и
$\frac{\partial^2 F_p}{\partial w_{ji}^2} = \phi''(U_p^{(2)})(w_{pj} \phi' (U_j^{(1)})x_iw_{ij})^2 + \phi' (U_p^{(2)})w_{pj} \phi'' (U_j^{(1)})(x_iw_{ij})^2$

4. вычисляем функцию выпуклости $S_i = \frac{w_i^2 H_i}{2}$ , находим $i$ , соответствующее наименьшей степени выпуклости.
5. вес $w_i$ удаляется из сети

Примеры на модельных данных

Пример 1: выборка линейно разделима

На графике показаны результаты классификации. На первом и втором слое сети - по 5 нейронов, количество признаков - 4. Итого получается 45 весов. Видно, что алгоритм сработал без ошибок.

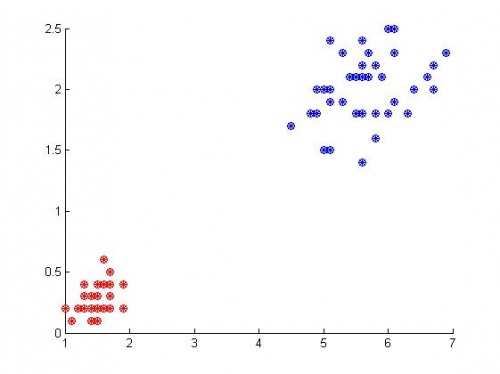
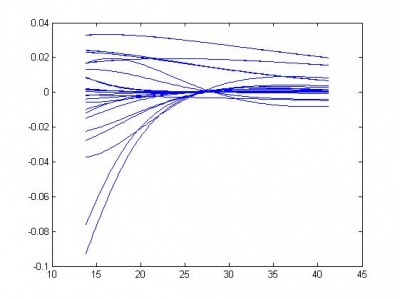
Ниже приведены графики функции выпуклости (одная кривая - зависимость функции выпуклости от одного параметра) и график зависимости ошибки от количества удаленных параметров.

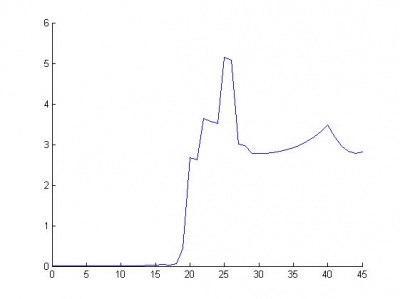
Видно, что из сети с 45 параметрами можно удалить 18, практически не проиграв в качестве.

Пример 2: выборка линейно неразделима

Те же самые 45 весов. Алгоритм допустил 3 ошибки при классификации:

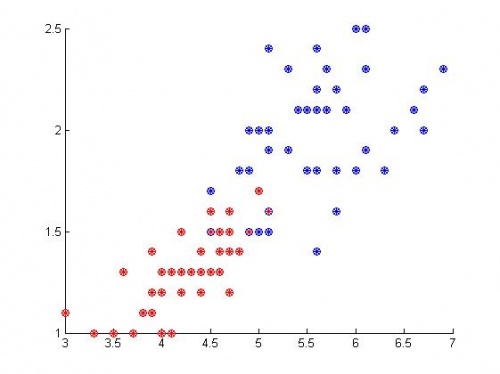
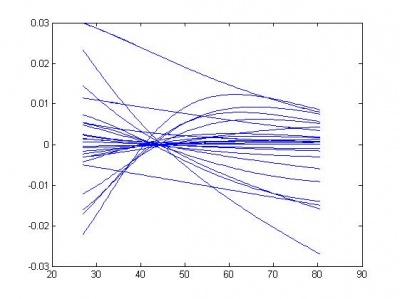
Графики функции выпуклости и количества ошибок:

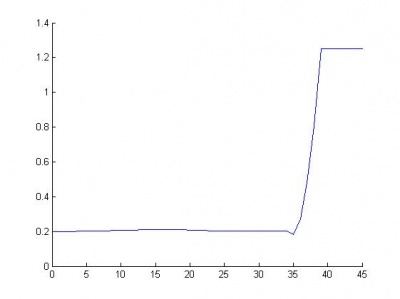
Результат прореживания здесь более наглядный: можно удалить 35 из 45 параметров без потери качества.

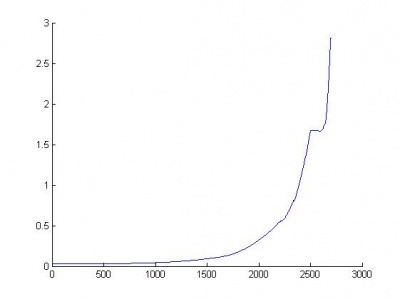
Приведем график зависимости ошибки от количества удаленных параметров для тех же данных и 50 нейронов на каждом из слоев.

Исходный код

Скачать листинги алгоритмов можно здесь: ComputeHessianAndConvexity.m, ComputeResult.m, PlotErrors.m,PlotHessian.m, PlotOBD.m, TuneNet.m, mainNet.m

См. также

Литература

Хайкин С. Нейронные сети, полный курс. 2е издание, испр.
К. В. Воронцов, Лекции по линейным алгоритмам классификации

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D1%80%D0%B5%D0%B6%D0%B8%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%B4%D0%B2%D1%83%D1%85%D1%81%D0%BB%D0%BE%D0%B9%D0%BD%D0%BE%D0%B9_%D0%BD%D0%B5%D0%B9%D1%80%D0%BE%D0%BD%D0%BD%D0%BE%D0%B9_%D1%81%D0%B5%D1%82%D0%B8_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категория: Нейронные сети

@@ Строка 5: / Строка 5: @@
 == Настройка нейронной сети ==
-Двухслойная нейронная сеть состоит из одного скрытого слоя и выходного слоя. Каждый нейрон сети имеет сигмоидальную функции активации <tex>\phi(z) = 1 / (1 + e^{-z})</tex>. Значения признаков <tex>x^i</tex> поступают на вход первому (скрытому) слою сети с весовой матрицей <tex>W_1</tex>, выходы первого слоя поступают на вход второму с весовой матрицей <tex>W_2</tex>.На выходе второго слоя вычисляется вектор-функция <tex>\bf{F} = (F_1(x),...,F_P(x))</tex>, где <tex>P</tex> - количество нейронов на втором слое. Необходимо настроить параметры сети, используя алгоритм обратного распространения (back propagation). <tex>\bf{E}(\bf{w}) = \frac{1}{2N} \sum_{n = 1}^N \sum_{p = 1}^P(F_p(n) - Y_p(n))^2</tex> - нормированная среднеквадратичная ошибка. Пусть <tex>w_{ji}</tex> - вес, соединяющий нейрон <tex>i </tex> с нейроном <tex>j</tex> следующего слоя. Тогда коррекция веса, применяемая к <tex>w_{ji}(n)</tex>, определяется согласно правилу <tex>\Delta w_{ji} = \eta \bf{\delta}_j(n)y_i(n)</tex>, где <tex>\bf{\delta}_j(n) = - \frac{\partial \bf{E}(n)}{\partial y_j(n)}\phi_j'(v_j(n))</tex> - локальный градиент нейрона j. Здесь <tex>y_i(n)</tex> - выход i-го нейрона, <tex>v_j(n) = \sum_{i = 1}^m w_{ji}(n)y_i(n)</tex> - значение, которое получает на вход функция активации, соответствующая j-му нейрону (m - количество его входов), <tex>\eta</tex> - темп обучения. Поскольку ошибка представляется в виде <tex>\bf{E}(n) = \frac{1}{2}\sum_{p = 1}^P (F_p(n) - y_p(n))^2</tex>, то для выходного слоя <tex>\frac {\partial \bf{E}(n)}{\partial y_j(n)} = y_j(n) - F_j(n) =: e_j(n)</tex>, и для него справедливо <tex>\Delta w_{ji} = - \eta e_j(n)\phi_j'(v_j(n))y_i(n)</tex>.
+Двухслойная нейронная сеть состоит из одного скрытого слоя и выходного слоя. Каждый нейрон сети имеет сигмоидальную функции активации <tex>\phi(z) = 1 / (1 + e^{-z})</tex>. Значения признаков <tex>x^i</tex> поступают на вход первому (скрытому) слою сети с весовой матрицей <tex>W</tex>, выходы первого слоя поступают на вход второму с весовой матрицей <tex>K</tex>.На выходе второго слоя вычисляется вектор-функция <tex>\bf{F} = (F_1(x),...,F_P(x))</tex>, где <tex>P</tex> - количество нейронов на втором слое. Необходимо настроить параметры сети, используя алгоритм обратного распространения (back propagation). <tex>\bf{E}(\bf{w}) = \frac{1}{2N} \sum_{n = 1}^N \sum_{p = 1}^P(F_p(n) - Y_p(n))^2</tex> - нормированная среднеквадратичная ошибка. Пусть <tex>w_{ji}</tex> - вес, соединяющий нейрон <tex>i </tex> с нейроном <tex>j</tex> следующего слоя. Тогда коррекция веса, применяемая к <tex>w_{ji}(n)</tex>, определяется согласно правилу <tex>\Delta w_{ji} = \eta \bf{\delta}_j(n)y_i(n)</tex>, где <tex>\bf{\delta}_j(n) = - \frac{\partial \bf{E}(n)}{\partial y_j(n)}\phi_j'(v_j(n))</tex> - локальный градиент нейрона j. Здесь <tex>y_i(n)</tex> - выход i-го нейрона, <tex>v_j(n) = \sum_{i = 1}^m w_{ji}(n)y_i(n)</tex> - значение, которое получает на вход функция активации, соответствующая j-му нейрону (m - количество его входов), <tex>\eta</tex> - темп обучения. Поскольку ошибка представляется в виде <tex>\bf{E}(n) = \frac{1}{2}\sum_{p = 1}^P (F_p(n) - y_p(n))^2</tex>, то для выходного слоя <tex>\frac {\partial \bf{E}(n)}{\partial y_j(n)} = y_j(n) - F_j(n) =: e_j(n)</tex>, и для него справедливо <tex>\Delta w_{ji} = - \eta e_j(n)\phi_j'(v_j(n))y_i(n)</tex>.
 Соответственно, для первого, скрытого, слоя справедлива формула обратного распространения <tex>\delta_j(n) = \phi_j'(v_j(n)) \sum_{p = 1}^P \delta_p(n) w_{pj}(n) </tex>.