SVM регрессия (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 1: Строка 1:
'''SVM (Support Vector Machine, [[машина опорных векторов]])''' — это особый класс алгоритмов, который характеризуется использованием ядер, отсутствием локальных минимумов, и т. д.
'''SVM (Support Vector Machine, [[машина опорных векторов]])''' — это особый класс алгоритмов, который характеризуется использованием ядер, отсутствием локальных минимумов, и т. д.
 +
 +
 +
== Постановка задачи ==
 +
 +
'''Дано:''' Обучающая выборка <tex>X=\{(x_i,y_i)\}_{i=1}^{\ell}</tex>, где <tex>x_i</tex>-признаковое описание i-го объекта, <tex>y_i</tex> - характеристика, приписываемая объекту. Функция потерь имеет вид <tex>a(x_i)=\mid (w,f(x_i))-w_0-y_i \mid_\epsilon</tex> для каждого вектора <tex>(x_i,y_i)</tex>, где <tex>\mid z \mid_\epsilon = max(0,\mid z \mid-\epsilon)</tex>.
 +
 +
'''Найти:''' такую функцию&nbsp;<tex>f_0</tex>, которая описывает зависимость <tex>E(y|\mathbf{x})=f_0(\mathbf{x})</tex> наилучшим образом.
 +
 +
== Алгоритм ==
 +
{{Main|Машина опорных векторов}}
 +
В этом примере решается задача построения линейной SVM регрессии. Для этого решается прямая задача минимизации функционала потерь, в предположении что решение задается линейной комбинацией неких порождающих функций
 +
::<tex>Q_\epsilon(a,X)=\sum_{i=1}^\ell \mid (w,f(x_i))-w_0-y_i \mid_\epsilon + \tau (w,w)^2 \rightarrow \underset{w,w_0}{min}</tex>
 +
Для этого вводятся обозначение <tex>C=\frac{1}{2\tau}</tex> и дополнительные переменные <tex>\xi_i^+</tex> и <tex>\xi_i^-</tex>:
 +
 +
::<tex>\xi_i^+=(a(x_i)-y_i-\epsilon)_+</tex>, <tex>\xi_i^-=(-a(x_i)+y_i-\epsilon)_-</tex>, <tex>i=1,...,l</tex>.
 +
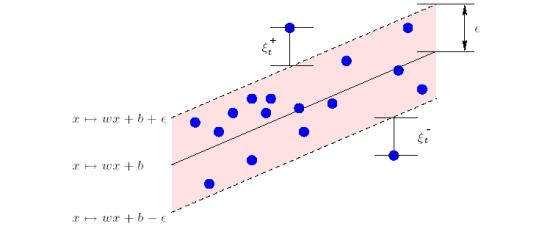
Геометрический смысл <tex>\xi_i^+</tex> и <tex>\xi_i^-</tex>:
 +
 +
[[Изображение:GeometricalSenceOfKsi.jpg]]
 +
 +
Далее решается задача квадратичного программирования:
 +
 +
<tex>
 +
\begin{cases}
 +
\frac{1}{2} (w,w)^2 + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\
 +
(w,f(x_i))-w_0 \le y_i + \epsilon + \xi_i^+, & i=1,..,\ell; \\
 +
(w,f(x_i))-w_0 \ge y_i - \epsilon - \xi_i^-, & i=1,..,\ell; \\
 +
\xi_i^- \ge 0, \mbox{ } i=1,..,\ell; \\
 +
\xi_i^+ \ge 0, \mbox{ } i=1,..,\ell; \\
 +
\end{cases}
 +
</tex>
 +
 +
Эту же задачу можно преобразовать к виду <tex>\frac{1}{2}u^T H u + g u\rightarrow \underset{u}{min}</tex>, при условии, что <tex>A u \le b,\ </tex>а также, <tex>lb \le u</tex>, где <tex>u</tex> - вектор-столбец, составленный из столбцов <tex>w\ , \xi_i^+, \xi_i^-</tex>, тоесть, где все переменные объеденены в один столбец неизвестных. В таких обозначениях <tex>H=diag(1,1,...,1,0,0,...,0),\ g=(0,0,...,0,1,1,...,1)</tex>, где единиц и нулей в <tex>H</tex> и <tex>g</tex> соответственно столько же, сколько порождающих фукций, а размерность матрицы <tex>H</tex> и вектора <tex>g</tex> равна размерности <tex>u</tex>.
 +
 +
Теперь построим матрицу А и столбцы <tex>b</tex> и <tex>lb</tex>. Преобразуем задачу квадратичного программирования к виду
 +
 +
<tex>
 +
\begin{cases}
 +
\frac{1}{2} (w,w)^2 + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\
 +
(w,f(x_i)) + w_0 -\xi_i^+ \le y_i + \epsilon , & i=1,..,\ell; \\
 +
-(w,f(x_i))+ w_0 -\xi_i^- \le -y_i + \epsilon , & i=1,..,\ell; \\
 +
0 \le \xi_i^-, \mbox{ } i=1,..,\ell; \\
 +
0 \le \xi_i^+, \mbox{ } i=1,..,\ell; \\
 +
\end{cases}
 +
</tex>
 +
 +
Отсюдого получаем,
 +
<tex>
 +
A=\begin{Vmatrix}
 +
f^T(\x_1) & -1 & 0 & \cdots & 0 \\
 +
f^T(\x_2) & 0 & -1 & \cdots & 0 \\
 +
\vdots & \vdots &\vdots & \ddots & \vdots \\
 +
f^T(\x_\ell) & 0 & 0 & \vdots & 0 \\
 +
-f^T(\x_1) & 0 & 0 & \vdots & 0 \\
 +
\vdots & \vdots &\vdots & \ddots & \vdots \\
 +
-f^T(\x_\ell) & 0 & 0 & \cdots & -1 \\
 +
\end{Vmatrix},\ b=
 +
\begin{Vmatrix}
 +
y_1 + \epsilon \\
 +
y_2 + \epsilon \\
 +
\vdots \\
 +
y_\ell + \epsilon \\
 +
-y_1 + \epsilon \\
 +
\vdots \\
 +
-y_\ell + \epsilon \\
 +
\end{Vmatrix},\ lb=
 +
\begin{Vmatrix}
 +
-\infty \\
 +
-\infty \\
 +
\vdots \\
 +
-\infty \\
 +
0 \\
 +
\vdots \\
 +
0 \\
 +
\end{Vmatrix}
 +
</tex>, и количество минус бесконечностей в lb равно количеству порождающих функций, а количество нулей равно <tex>2\ell</tex>.
{{Задание|Алексей Корниенко|В.В.Стрижов|28 мая 2010}}
{{Задание|Алексей Корниенко|В.В.Стрижов|28 мая 2010}}

Версия 20:39, 28 апреля 2010

SVM (Support Vector Machine, машина опорных векторов) — это особый класс алгоритмов, который характеризуется использованием ядер, отсутствием локальных минимумов, и т. д.


Постановка задачи

Дано: Обучающая выборка X=\{(x_i,y_i)\}_{i=1}^{\ell}, где x_i-признаковое описание i-го объекта, y_i - характеристика, приписываемая объекту. Функция потерь имеет вид a(x_i)=\mid (w,f(x_i))-w_0-y_i \mid_\epsilon для каждого вектора (x_i,y_i), где \mid z \mid_\epsilon = max(0,\mid z \mid-\epsilon).

Найти: такую функцию f_0, которая описывает зависимость E(y|\mathbf{x})=f_0(\mathbf{x}) наилучшим образом.

Алгоритм

Основная статья: Машина опорных векторов

В этом примере решается задача построения линейной SVM регрессии. Для этого решается прямая задача минимизации функционала потерь, в предположении что решение задается линейной комбинацией неких порождающих функций

Q_\epsilon(a,X)=\sum_{i=1}^\ell \mid (w,f(x_i))-w_0-y_i \mid_\epsilon + \tau (w,w)^2 \rightarrow \underset{w,w_0}{min}

Для этого вводятся обозначение C=\frac{1}{2\tau} и дополнительные переменные \xi_i^+ и \xi_i^-:

\xi_i^+=(a(x_i)-y_i-\epsilon)_+, \xi_i^-=(-a(x_i)+y_i-\epsilon)_-, i=1,...,l.

Геометрический смысл \xi_i^+ и \xi_i^-:

Изображение:GeometricalSenceOfKsi.jpg

Далее решается задача квадратичного программирования:

\begin{cases} \frac{1}{2} (w,w)^2 + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\ (w,f(x_i))-w_0 \le y_i + \epsilon + \xi_i^+, & i=1,..,\ell; \\ (w,f(x_i))-w_0 \ge y_i - \epsilon - \xi_i^-, & i=1,..,\ell; \\ \xi_i^- \ge 0, \mbox{ } i=1,..,\ell; \\ \xi_i^+ \ge 0, \mbox{ } i=1,..,\ell; \\ \end{cases}

Эту же задачу можно преобразовать к виду \frac{1}{2}u^T H u + g u\rightarrow \underset{u}{min}, при условии, что A u \le b,\ а также, lb \le u, где u - вектор-столбец, составленный из столбцов w\ , \xi_i^+, \xi_i^-, тоесть, где все переменные объеденены в один столбец неизвестных. В таких обозначениях H=diag(1,1,...,1,0,0,...,0),\ g=(0,0,...,0,1,1,...,1), где единиц и нулей в H и g соответственно столько же, сколько порождающих фукций, а размерность матрицы H и вектора g равна размерности u.

Теперь построим матрицу А и столбцы b и lb. Преобразуем задачу квадратичного программирования к виду

\begin{cases} \frac{1}{2} (w,w)^2 + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\ (w,f(x_i)) + w_0 -\xi_i^+ \le y_i + \epsilon , & i=1,..,\ell; \\ -(w,f(x_i))+ w_0 -\xi_i^- \le -y_i + \epsilon , & i=1,..,\ell; \\ 0 \le \xi_i^-, \mbox{ } i=1,..,\ell; \\ 0 \le \xi_i^+, \mbox{ } i=1,..,\ell; \\ \end{cases}

Отсюдого получаем, A=\begin{Vmatrix} f^T(\x_1) & -1 & 0 & \cdots & 0 \\ f^T(\x_2) & 0 & -1 & \cdots & 0 \\ \vdots & \vdots &\vdots & \ddots & \vdots \\ f^T(\x_\ell) & 0 & 0 & \vdots & 0 \\ -f^T(\x_1) & 0 & 0 & \vdots & 0 \\ \vdots & \vdots &\vdots & \ddots & \vdots \\ -f^T(\x_\ell) & 0 & 0 & \cdots & -1 \\ \end{Vmatrix},\ b= \begin{Vmatrix} y_1 + \epsilon \\ y_2 + \epsilon \\ \vdots \\ y_\ell + \epsilon \\ -y_1 + \epsilon \\ \vdots \\ -y_\ell + \epsilon \\ \end{Vmatrix},\ lb= \begin{Vmatrix} -\infty \\ -\infty \\ \vdots \\ -\infty \\ 0 \\ \vdots \\ 0 \\ \end{Vmatrix} , и количество минус бесконечностей в lb равно количеству порождающих функций, а количество нулей равно 2\ell.


Данная статья является непроверенным учебным заданием.
Студент: Участник:Алексей Корниенко
Преподаватель: Участник:В.В.Стрижов
Срок: 28 мая 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=SVM_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты