Прогнозирование ежедневных цен на электроэнергию (отчет)
Материал из MachineLearning.
м (→Локальный алгоритм Федоровой) |
|||
| Строка 490: | Строка 490: | ||
}} | }} | ||
| - | {{ | + | {{ЗаданиеВыполнено|Зайцев Алексей|В.В. Стрижов|15 декабря 2009|Likz|Strijov|}} |
__NOTOC__ | __NOTOC__ | ||
Версия 14:58, 28 мая 2010
Введение
Эта статья является сильно сокращенным вариантом статьи Daily electricity price forecasting (report).
Описание проекта
Цель проекта
Цель проекта - прогнозирование ежедневных цен на электричество. Горизонт прогнозирования - один месяц.
Обоснование проекта
Полученные данные могут быть использованы для хеджинга или другой игры на свободном рынке цен на электричество.
Описание данных
У нас есть данные с 01/01/2003 до сегодняшнего дня. Данные для прогнозирования состоят из временного ряда, различных погодных параметров (температура, скорость ветра, относительная влажность, ...) и средних цен на электричество.
Критерии качества
Критерием качества служит скользящий контроль. Мы разбиваем данные на основную выборку - все данные без данных за последний месяц и контрольную выборку - данные за последний месяц. Эту процедуру можно повторить для всех месяцев полседнего года. Целевая функция MAPE (средняя абсолютная ошибка в процентах) для посленего месяца.
Требования к проекту
Месячная ошибка для нашего алгоритма должна быть меньше ошибки для алгоритма заказчика (LASSO).
Выполнимость проекта
В данных отсутствует информация о пиках, предсказание которых является отдельной задачей.
Используемые методы
Мы испольуем предположение о линейной зависимости откликов от признаков или их различных производных. Также модель должна использовать периодичность конечных данных.
Постановка задачи
У нас есть временной ряд из матрицы признаков и вектора
ответов. Нам необходимо восстановить вектор ответов
по матрице признаков
. Известно, что временной ряд, который необходимо восстановить идет непосредственно после временного ряда, ответы для которого нам известны.
Предлагается использовать функционал качества MAPE:
-
,
где -- восстановленные ответы, а
-- правильные ответы.
Описание алгоритмов
Для решения предложенной задачи было выбрано 2 алгоритма - LARS и локальный алгоритм, вариация метода k ближайших соседей. Были использованы различные модификации для улучшения работы алгоритма на реальных данных. Мы применяли преобразования начальных признаков, ядерное сглаживание, фильтрацию выбросов и нормализацию.
Описание системы
Цель этого раздела -- описание системной архитектуры проекта.
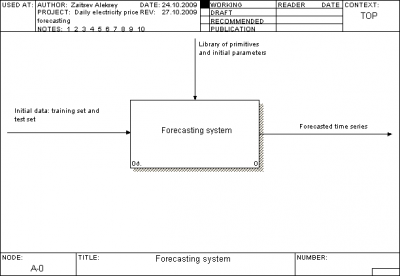
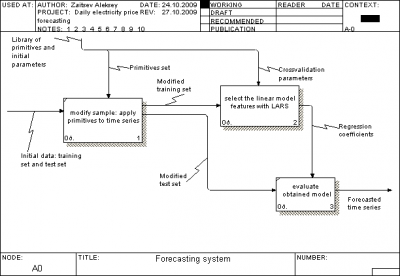
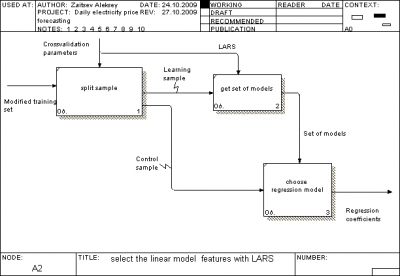
Общий взгляд на систему
Описание архитектуры проекта
Мы использовали стандарт IDEF0 для описания архитектуры проекта.
Описание данных
Для всех алгоритмов мы использовали данные из файла DayElectricityPrice.mat, содержащего
| Name | Size | Description |
|---|---|---|
| xRegression | | матрица переменных |
| yRegression | | матрица откликов |
Каждый элемент матрицы -- целое либо действительное число, первый столбец каждой матрицы -- временной ряд.
Для алгоритмов DOW LARS и LARS мы модифицировали данные следующим образом:
| Имя | Размер | Описание |
|---|---|---|
| trainingX | | обучающая матрица переменных |
| trainingY | | обучающий вектор откликов |
| testX | | контрольная матрица переменных |
| model | | вектор параметров алгоритма |
Для локального алгоритма Федоровой мы использовали следующие структуры:
| Имя | Размер | Описание |
|---|---|---|
| trainingY | | обучающий вектор откликов |
| testX | int | горизонт прогнозирования |
| | | параметры алгоритма |
Описание модулей
| Алгоритм | MATLab файл | Описание |
|---|---|---|
| LARS | LARS.m,modLARS.m | реализует LARS |
| Local algorithm Fedorovoy | kMeans.m | реализует LAF |
Каждый модуль снабжен комментариями и файлом Demo.m -- демонстрация возможностей его работы.
Отчет о вычислительном эксперименте
Визуальный анализ
Модельные данные
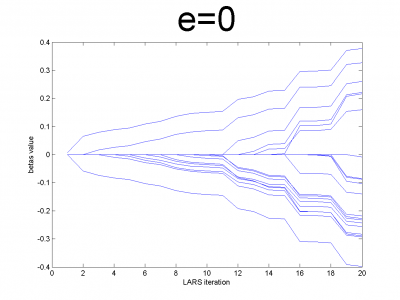
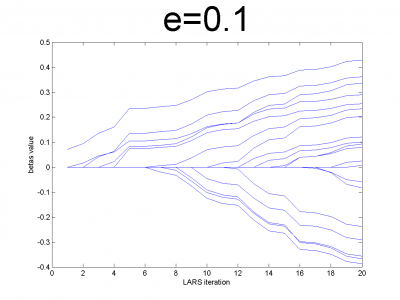
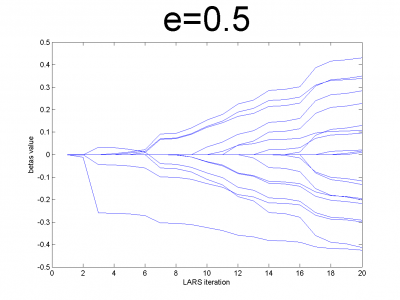
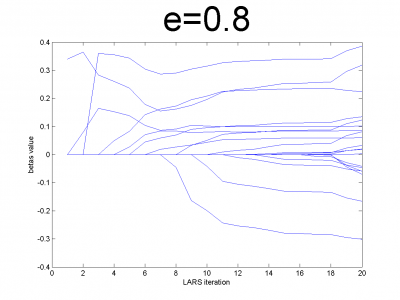
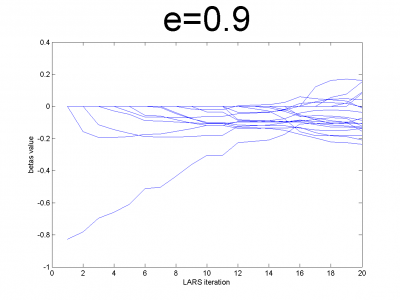
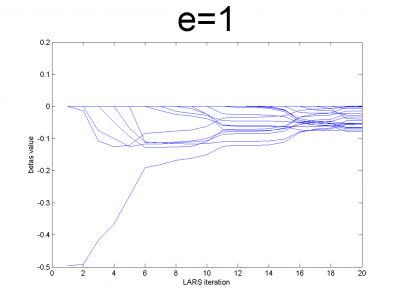
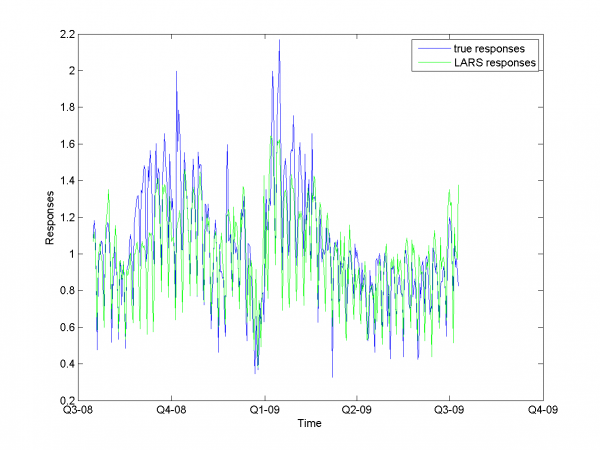
Проверим корректность работы LARS на модельных данных и его свойство ухудшать прогноз для плохо обусловленных матриц. Модельные данные создаются на основе кода, приведенного ниже:
n = 100; m = 20; X = e*ones(n,m)+(1-e)*[diag(ones(m,1));zeros(n-m,m)]; beta = (rand(m,1)-0.5); Y = X*beta; X = X + (rand(n,m) - 0.5)/10;
Для различных значений мы получили плохо и хорошо обусловленные матрицы. Мы использовали
. Для небольших значений
матрица хорошо обусловлена и имеет практически нулевую корреляцию признаков. Для значений
близких к 1, мы получим матрицу состоящую только из единиц с небольшим шумом. Она плохо обусловлена. Направления векторов корреляции почти совпадают.
Эксперимент показывает, что реализованный нами алгоритм обладает предложенным свойством.
Описание данных
В нашей задаче мы используем следующие данные - матрицу переменных xRegression и вектор откликов yRegression. Мы будем обозначать их X и Y соответственно. Размер X
-- , где
-- количество объектов (временной ряд дней), а
-- количество переменных. Размер Y
--
.
Первый столбец и
-- временной ряд. Второй столбец
-- вектор откликов. Они нормализованы на среднегодичное значение. Количество переменных в
-- 26. Они представлены в таблице ниже.
| # | Описание |
|---|---|
| 1 | временной ряд |
| 2-6 | день недели |
| 7-18 | месяц |
| 19 | средняя температура |
| 20 | индекс HDD |
| 21 | индексCDD |
| 22 | максимальная температура |
| 23 | минимальная температура |
| 24 | относительная влажность |
| 25 | осадки |
| 26 | скорость ветра |
Эксперимент с LARS
Для данных нашей задачи мы провели ряд вычислительных экспериментов. Для каждого эксперимента мы посчитали MAPE.
В первом случае мы использовали для решения задачи обычный LARS и не модифицированные данные.
model = [1,1,0,0,0,0,0,0,0]; % model parameters
Среднее значение MAPE для всех месяцев -- 16.64%.
Во втором эксперименте мы модифицировали матрицу признаков, добавив квадраты и корни начальных переменных.
model = [1,1,1,0,0,0,0,0,0]; % model parameters
Средняя MAPE для всех месяцев равняется 17.20%.
В третьем эксперименте мы использовали сглаженные и индикаторные переменные.
model = [1,0,0,1,0,0,0,0,0]; % model parameters
Средняя MAPE получилась равной 17.16%.
В следующем эксперименте мы использовали сглаженные и сглаженные квадраты переменных.
model = [1,0,0,1,1,0,0,0,0]; % model parameters
MAPE -- 19.2%.
В последнем эксперименте этого раздела мы использовали и сглаженные, и не сглаженные значения переменных
model = [1,1,1,1,0,0,0,0,0]; % model parameters
Мы получили MAPE 16.89% в этом эксперименте.
Полученные результаты позволяют говорить о том, что для такого набора переменных значение MAPE -- между 16% и 18%. Сглаживание не способно сильно повлиять на ситуацию. Необходимо попробовать исключить выбросы из данных, что бы улучшить прогноз.
Фильтрация выбросов
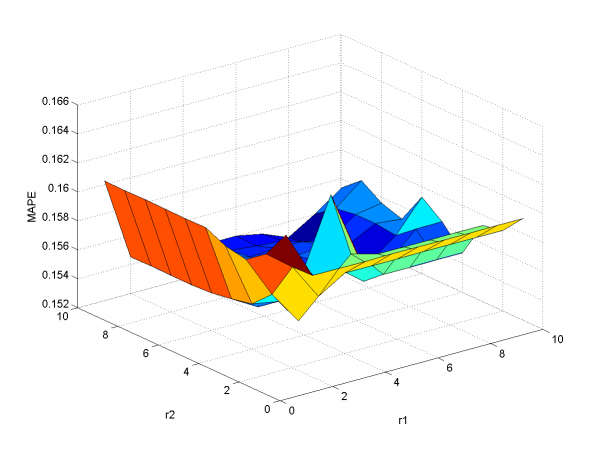
В этом разделе мы использовали фильтрацию выбросов. Для оптимизации параметров фильтрации использовалась двухмерная оптимизация.
В первом эксперименте мы использовали начальный набор переменных и фильтацию.
model = [1,1,0,0,0,0,0,0,0]; % model parameters
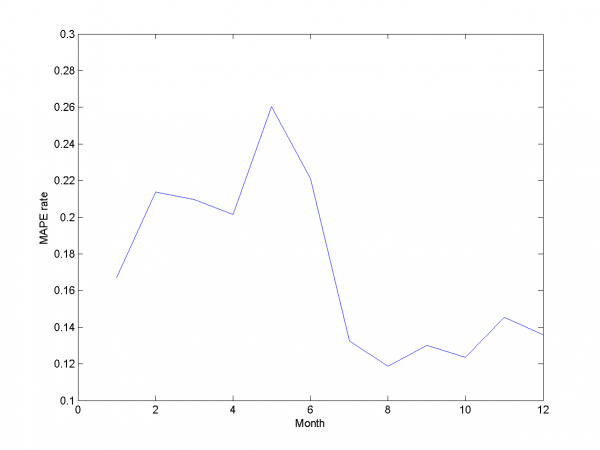
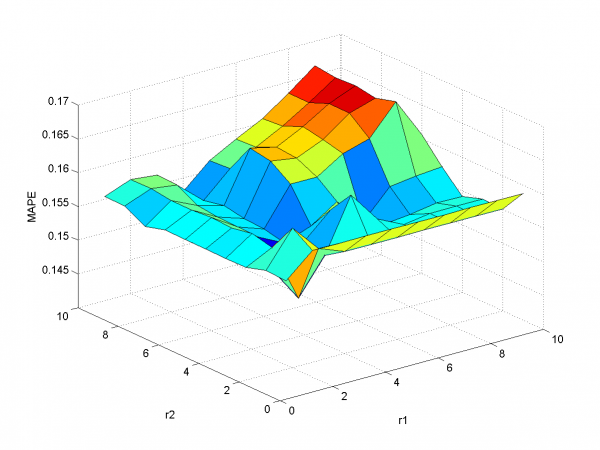
Минимальная MAPE равнаs 15.45\%( в точке
). Мы получили меньшее значение MAPE , чем раньше.
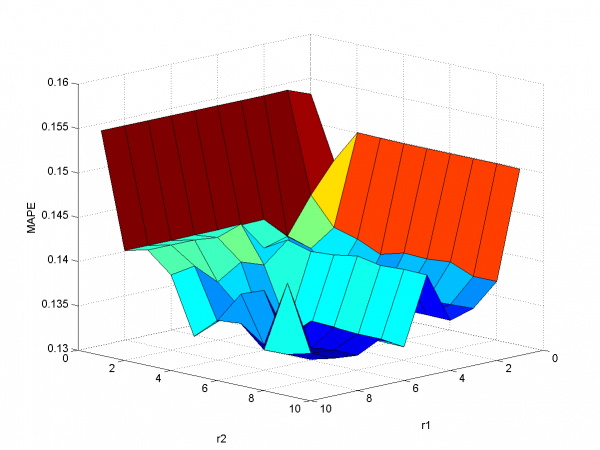
В следующем эксперименте мы использовали модифицированные и сглаженные переменные.
model = [1,1,1,1,0,0,0,0,0]; % model parameters
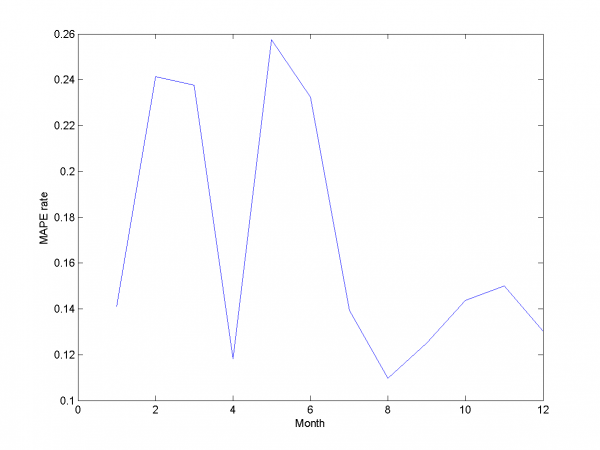
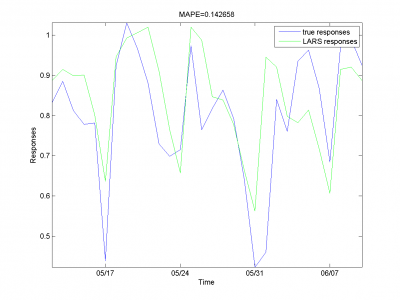
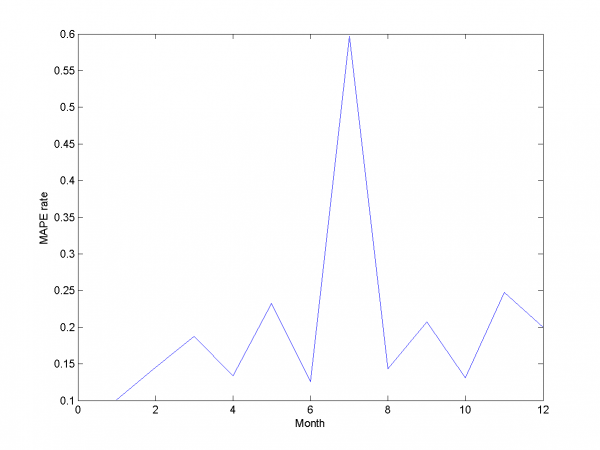
У функции MAPE локальный минимум в точке ,
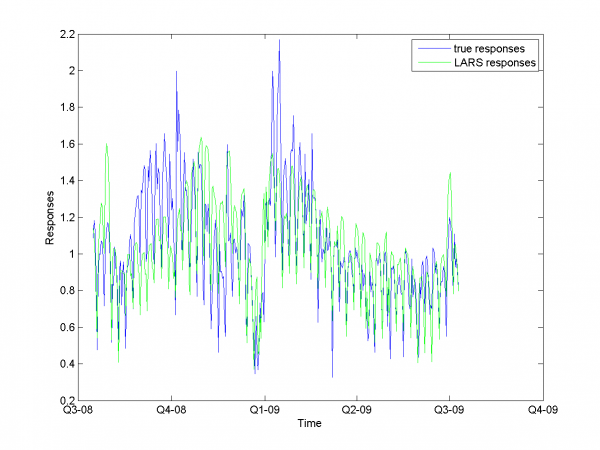
значение функции -- 15.29%. Ниже представлены результаты для оптимальных параметров фильтрации.
Мы получили результат лучше, чем в предыдущем разделе.
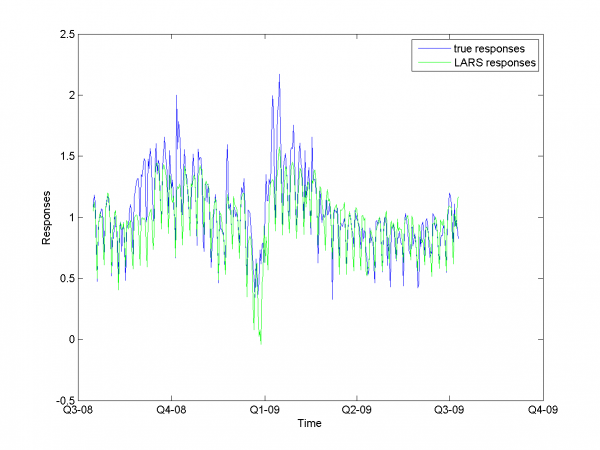
Авторегрессия
Давайте применим авторегрессию к решению этой задачи.
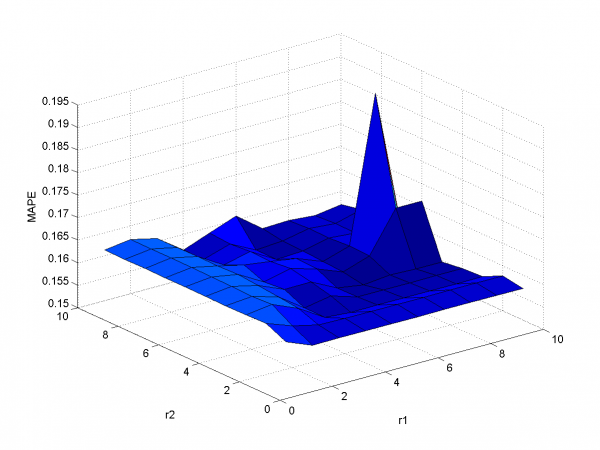
Как и раньше, для оптимизации мы используем двухмерную оптимизацию.
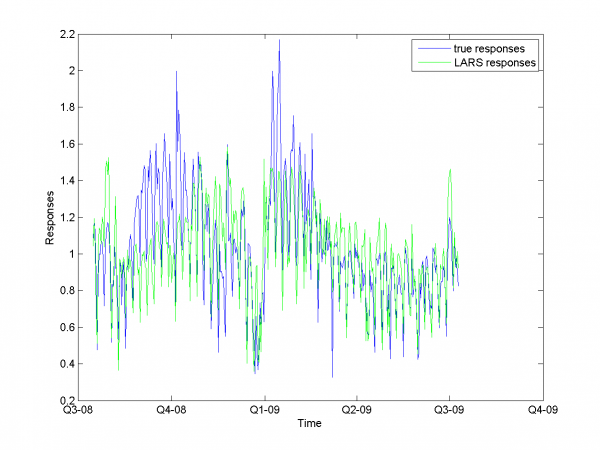
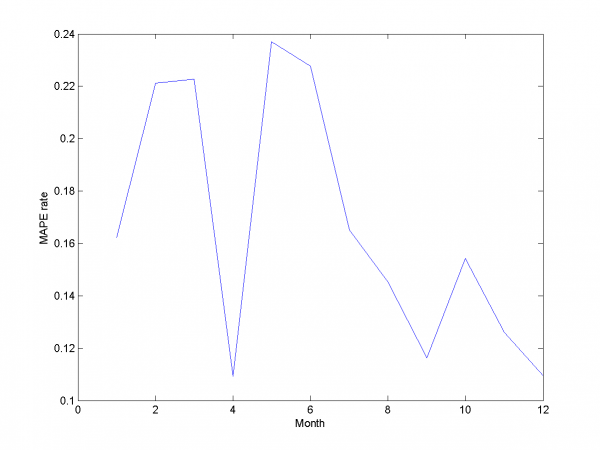
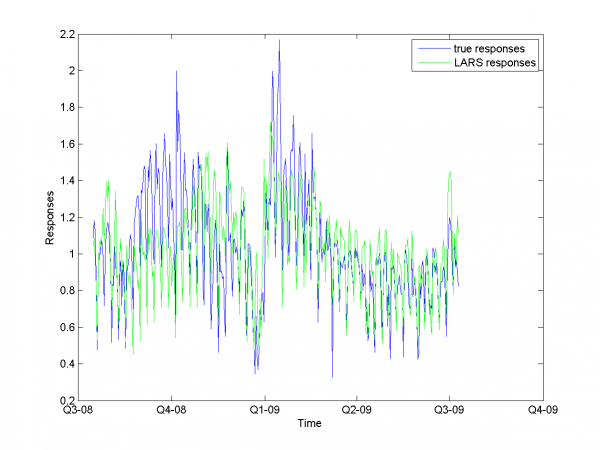
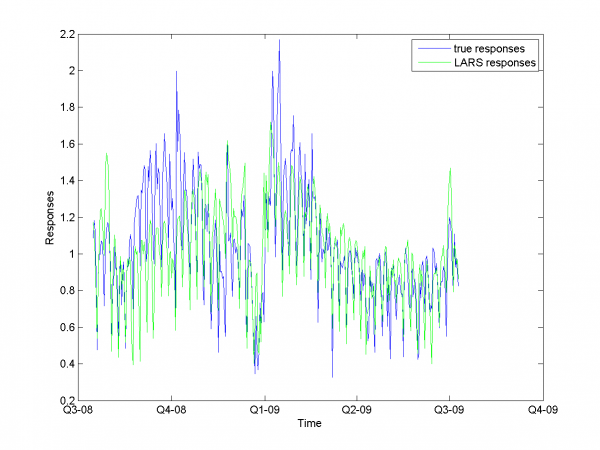
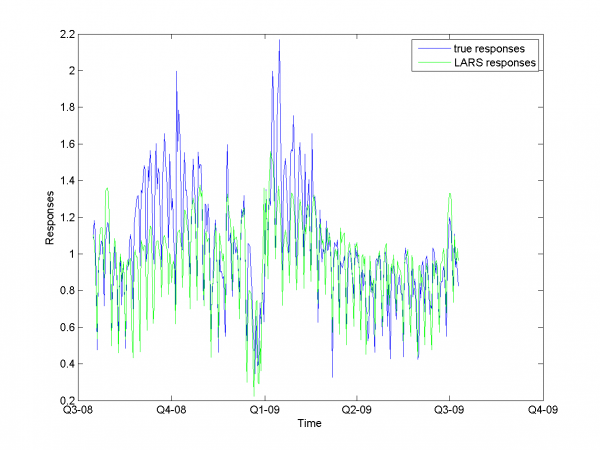
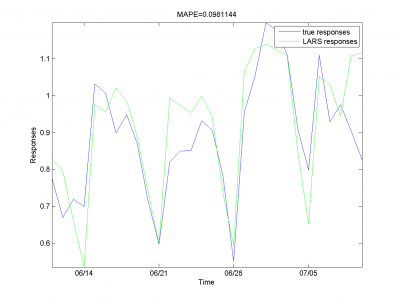
Минимум значения MAPE -- в точке .
Он равен 13.31%.
model = [1,1,1,1,0,0,0,0.7,0.8]; % model parameters
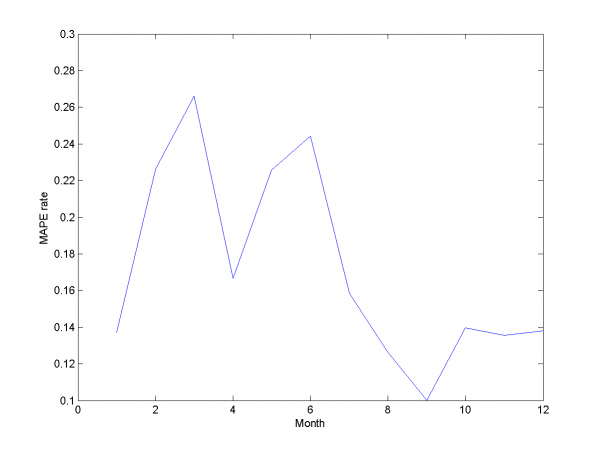
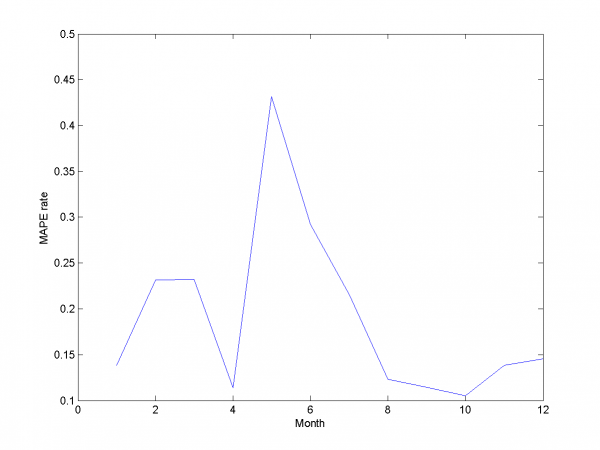
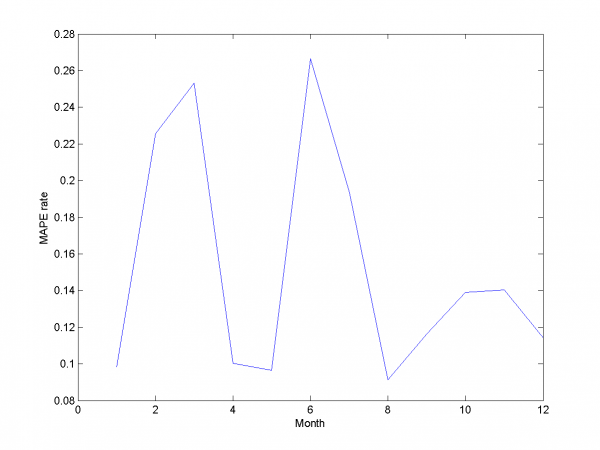
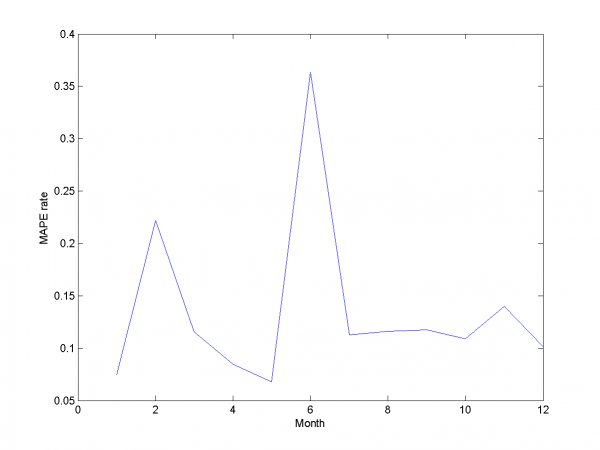
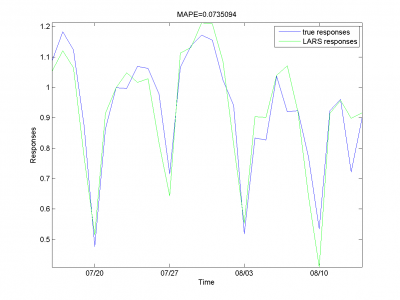
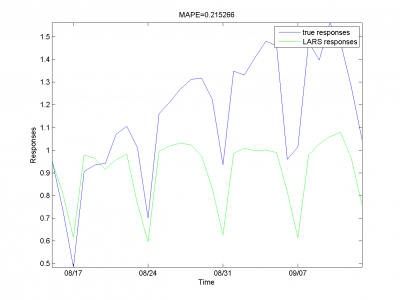
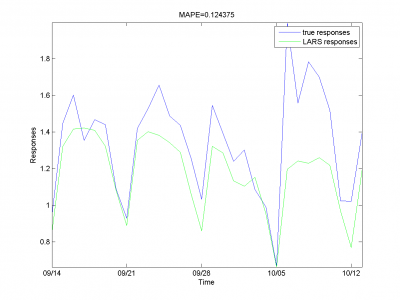
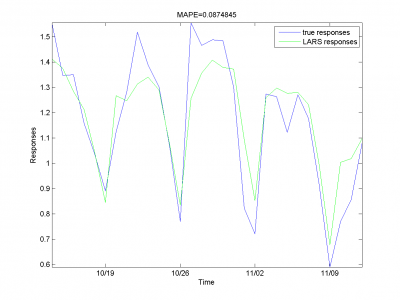
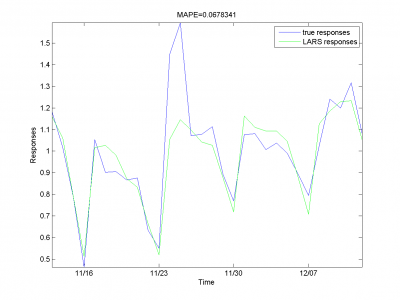
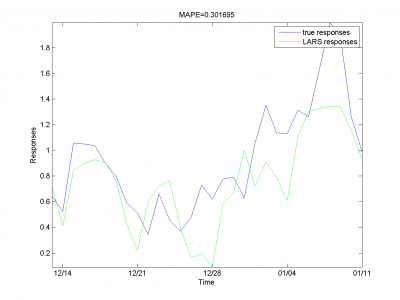
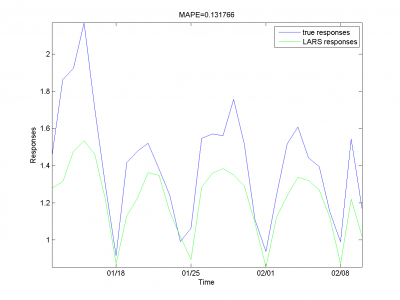
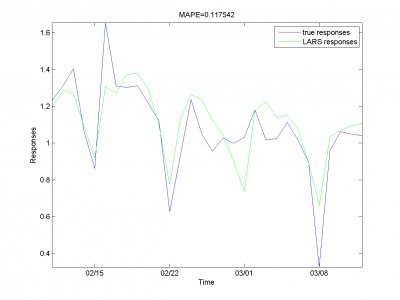
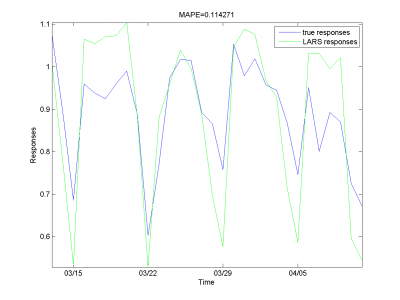
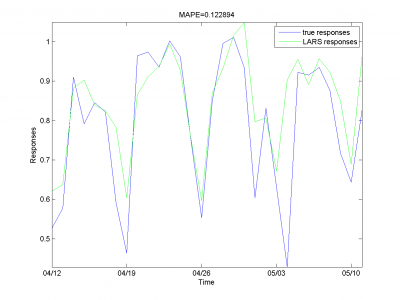
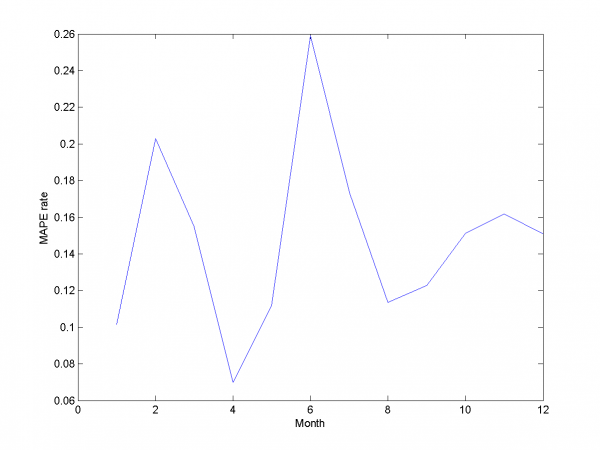
Для каждого месяца:
Этот результат -- лучший из полученных нами.
Набор моделей для каждого дня недели
В данном разделе мы используем периодику предложенных данных для создания более точного прогноза. Для каждого мы построим отдельную модель регрессии.
model = [1,1,1,1,0,0,0,0,0,s]; % model parameters
-- множитель для создания обучающей выборки. Ее размер
--
.
| Control set size | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|
| MAPE rate | 0.1740 | 0.1860 | 0.1790 | 0.1897 | 0.184 | 0.1826 | 0.1882 | 0.1831 | 0.1846 | 0.195 |
Мы видим, что улучшения за счет использования периодичности данных путем создания отдельных моделей для каждого дня недели добиться не удается.
Попробуем удалить выбросы из выборки и снова применить данную идею.
MAPE равняется 14.79\%.
model = [1,1,1,0,0,0,6,0.3,0.3,1]; % model parameters
Нам не удалось добиться улучшения качества прогнозирования путем создания отдельной модели для каждого дня недели.
Локальный алгоритм Федоровой
Мы используем алгоритм из работ (11) и (12). Мотивация для его использования -- наличие периодик в наших данных. Основная проблема -- наличие выбросов и шума в наших данных. В итоге мы получили результаты хуже, чем результаты для LARS.
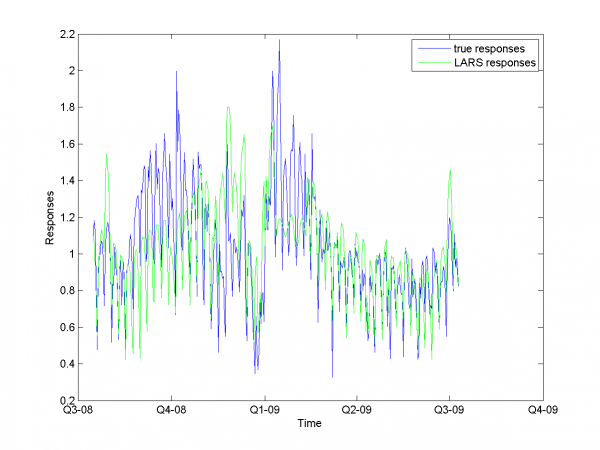
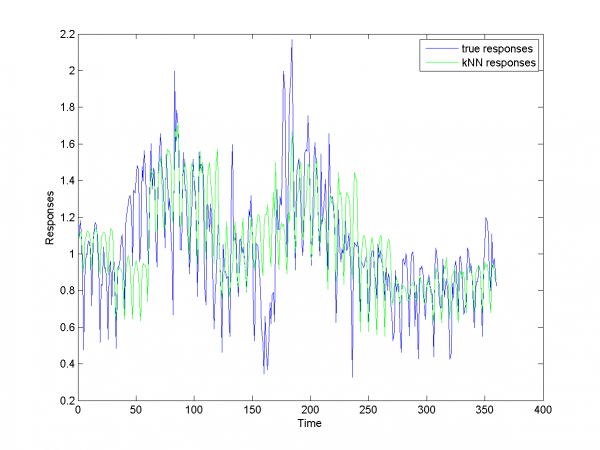
Процедура оптимизации параметров алгоритма быстро сходится и дает результаты, представленные ниже.
MAPE равняется 20.43%.
Сравнение алгоритмов
Подведем итог нашей работы. Вынесем результата работы наших алгоритмов в таблицу
| Algorithm | LARS | RS LARS | RS and autoLARS | DOW LARS | LAF |
|---|---|---|---|---|---|
| MAPE | 16.64% | 15.29% | 13.31% | 14.79% | 20.43% |
Две основные трудности при попытке создания регрессионных моделей для наших данных -- наличие выбросов, резких скачков в векторе ответов и слабая корреляция между представленными матрицами переменных и откликов.
Отчет о результатах
Для нашего лучшего алгоритма мы уменьшили MAPE на 4% по отношению к начальному алгоритму (Мы получили 13.31% по сравнению с начальными 17%). Что бы решить эту задачу мы применили различные дополнительные эвристики и модификации к LARS. Так же мы создали реализацию локального алгоритма к ближайших соседей и сравнили результаты работы наших алгоритмов с его результатом работы.
Смотри также
Daily electricity price forecasting (report)
Метод k ближайших соседей (пример)
Ссылки
Отчет о выполнении проекта, архитектура проекта и код алгоритмов
Литература
- Hsiao-Tien Pao A Neural Network Approach to m-Daily-Ahead Electricity Price Prediction. — 2006.
- Wei Wu, Jianzhong Zhou,Li Mo and Chengjun Zhu Forecasting Electricity Market Price Spikes Based on Bayesian Expert with Support Vector Machines. — 2006.
- S.Borovkova, J.Permana Modelling electricity prices by the potential jump-diffusion. — 2006.
- R.Weron, A.Misiorek Forecasting spot electricity prices: A comparison of parametric and semiparametric time series models. — 2008.
- J.Cherry, H.Cullen, M.Vissbeck, A.Small and C.Uvo Impacts of the North Atlantic Oscillation on Scandinavian Hydropower Production and Energy Markets. — 2005.
- Yuji Yamada Optimal Hedging of Prediction Errors Using Prediction Errors. — 2008.
- Wikipedia.
- Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani Least Angle Regression. — 2002.
- Robert Tibshirani Regression shrinkage selection and via the LASSO. — 1996.
- Vadim Strijov Model Generation and its Applications in Financial Sector. — 2009.
- J. McNames Innovations in local modeling for time series prediction. — 1996.
- В. Федорова Локальные методы прогнозирования временных рядов. — 2009.
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |