Теорема схемы
Материал из MachineLearning.
| Строка 32: | Строка 32: | ||
# Строго говоря, утверждение теоремы схем носит вероятностный характер (в левой части неравенства стоит математическое ожидание). Поэтому возможны отклонения от этого закона, а насколько они велики и вероятны - в теореме не указано. | # Строго говоря, утверждение теоремы схем носит вероятностный характер (в левой части неравенства стоит математическое ожидание). Поэтому возможны отклонения от этого закона, а насколько они велики и вероятны - в теореме не указано. | ||
# Комбинация двух "хороших" строительных блоков не всегда является "хорошей". Существуют примеры, когда такое комбинирование приводит к существенному снижению приспособленности схемы-блока. | # Комбинация двух "хороших" строительных блоков не всегда является "хорошей". Существуют примеры, когда такое комбинирование приводит к существенному снижению приспособленности схемы-блока. | ||
| - | Тем не менее, иногда гипотеза строительных блоков выполняется на практике. | + | Тем не менее, иногда гипотеза строительных блоков выполняется на практике. Далее следует пример. |
==Задача выбора признаков с помощью ГА== | ==Задача выбора признаков с помощью ГА== | ||
| - | + | ===Предварительные замечания=== | |
| + | Суть данной задачи ( см. [[Выбор признаков с помощью генетических алгоритмов (пример)]] ) позволяет предположить, что гипотеза строительных блоков выполняется. Действительно, схемы соответствуют наборам признаков. Тогда логично считать, что в большинстве случаев комбинация хороших наборов должна дать хороший набор. | ||
| + | ===Постановка вычислительного эксперимента=== | ||
| + | Данные порождались следующим образом (D - дисперсия, D=100): | ||
| + | <source lang="matlab"> | ||
| + | x = [ 1:0.5:20 ]'; | ||
| + | y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + sqrt( D ) * randn( size( x, 1 ), 1 ); | ||
| + | </source> | ||
| + | Выборка делилась на training и testing части в соотношении 60%:40% случайным образом. | ||
| + | Использовался следующий набор порождающих функций (всего 12): <br /> | ||
| + | <tex>1,\; x,\; x^2,\; log(x),\; x^3,\; x*log(x),\; x^4,\; x^2*log(x),\; x^2*cos(x),\; cos(x)*log(x),\; x*sin(x)*log(x),\; x^2*cos(x)*log(x).</tex> <br /> | ||
| + | В наборе не было следующих функций, участвовавших в порождении: <tex>sin(x),\; x^2*sin(x).</tex> <br /> | ||
| + | Задача решалась простым ГА. При этом менялось значение параметра Размер Популяции. | ||
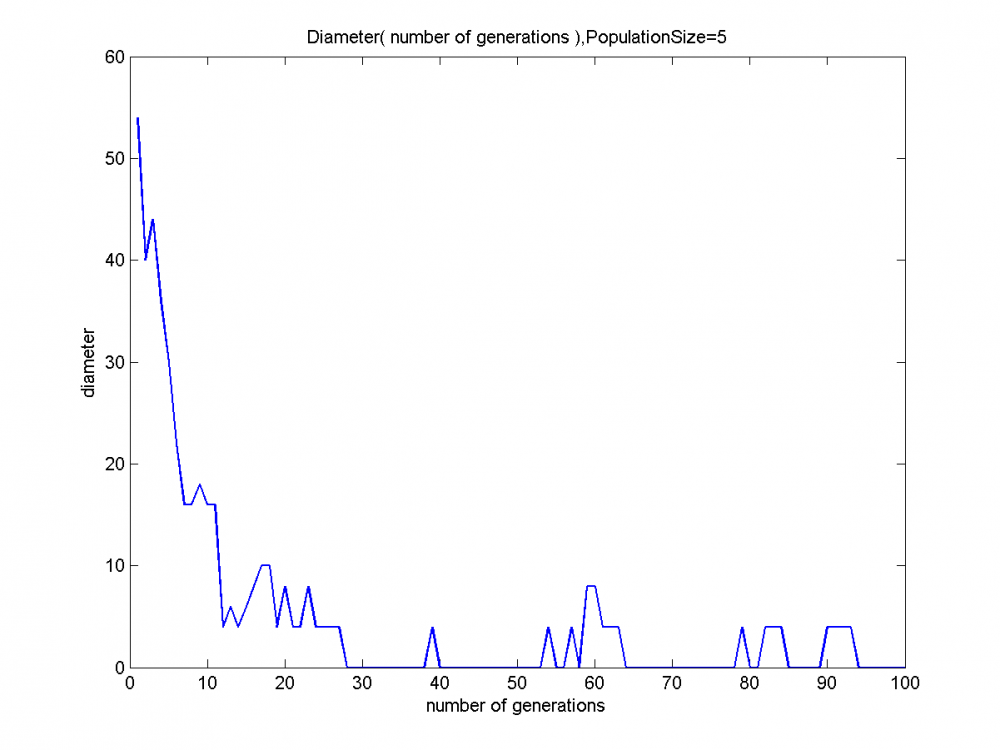
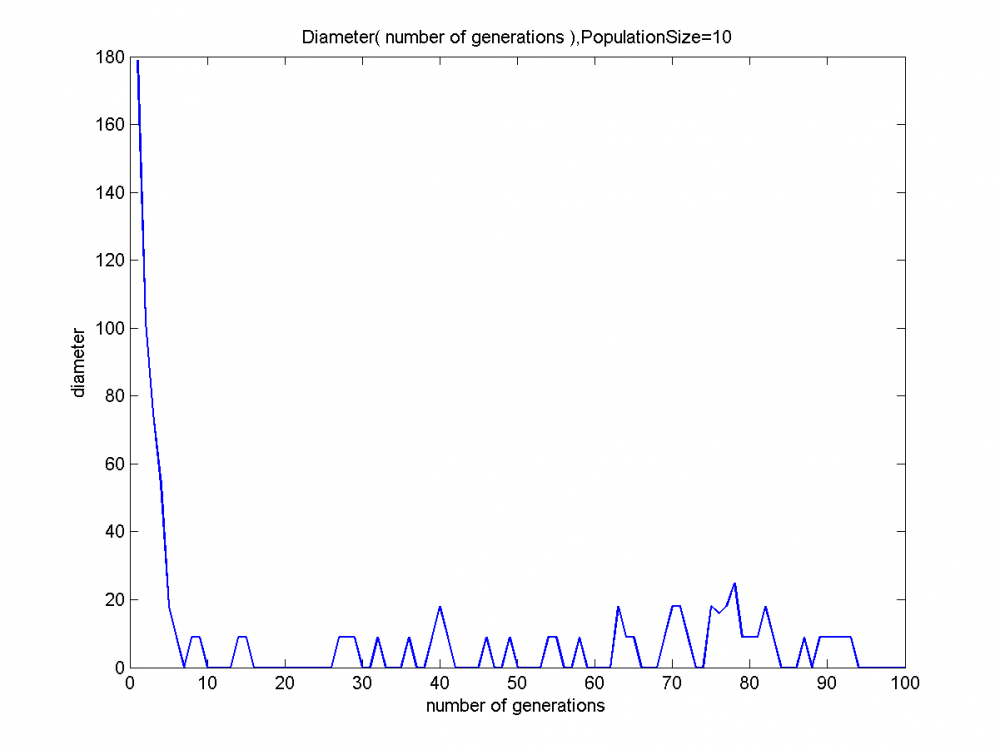
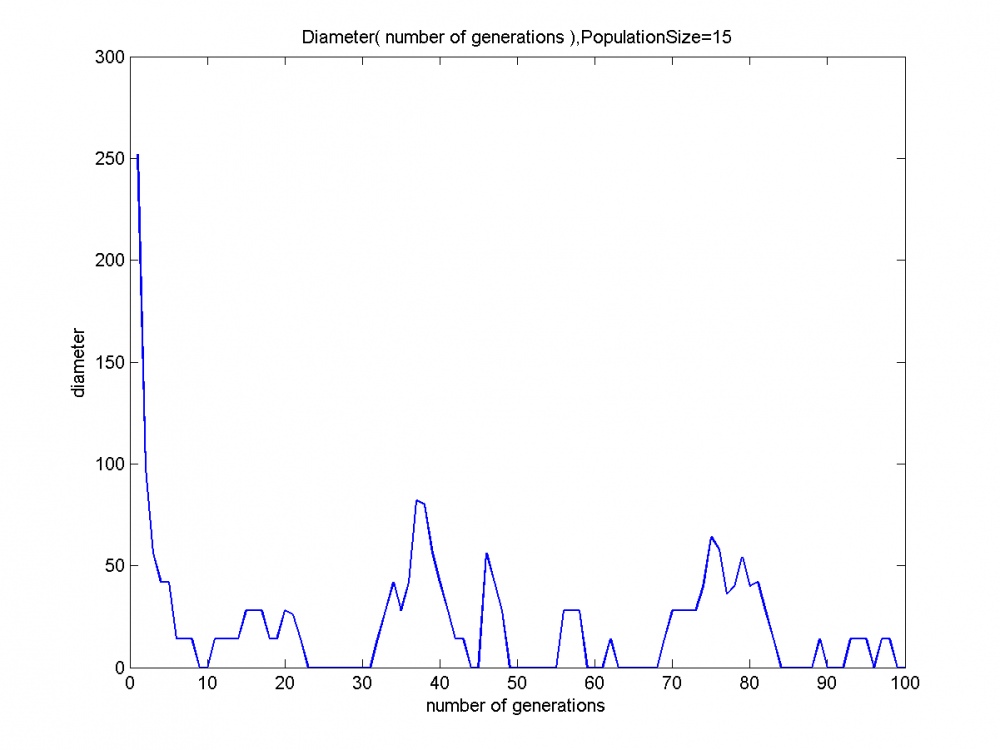
| + | ===Результаты=== | ||
| + | [[Изображение:Diameter( number of generations ),PopulationSize=5.png|1000px]] <br /> | ||
| + | [[Изображение:Diameter( number of generations ),PopulationSize=10.png|1000px]] <br /> | ||
| + | [[Изображение:Diameter( number of generations ),PopulationSize=15.png|1000px]] <br /> | ||
| + | ===Выводы=== | ||
| + | Вероятно, гипотеза строительных блоков в данном случае выполняется. | ||
{{Задание|Николай Савинов|В.В. Стрижов|20 июня 2010}} | {{Задание|Николай Савинов|В.В. Стрижов|20 июня 2010}} | ||
Версия 18:39, 5 июня 2010
Теорема схемы (англ. schema theorem) - теорема, описывающее действие генетического алгоритма (см. Генетический алгоритм) через понятие схемы. Каждой схеме соответствует некоторое подмножество особей в популяции. При определенных условиях, оговариваемых в теореме, будет выполняться экспоненциальный рост числа особей в этом подмножестве. Теорема была предложена Холландом, и это была первая успешная попытка объяснить действие генетического алгоритма.
Содержание |
Формулировка теоремы
Предположения и обозначения
Пусть используется простой генетический алгоритм, т. е. ГА с одноточечным кроссинговером и одноточечной мутацией.
Будем считать, что особью в популяции является бинарная строка длины . Если это не так, всегда можно закодировать ее нужным образом.
Введем следующие понятия:
- Схема - слово длины
в алфавите
, где
имеет смысл любого из символов
. В дальнейшем схема будет обозначаться
;
- Пример схемы - особь, удовлетворяющая схеме. Например, если схемой является
, то особь
является примером, а особь
- нет. Число примеров схемы H в обрабатываемой алгоритмом популяции в момент времени
(т. е. число особей популяции, удовлетворяющих схеме) будем обозначать как
;
- Порядок схемы
- число символов в схеме, не равных
;
- Определяющая длина схемы
- расстояние между крайними символами, не равными
;
- Степень приспособленности схемы
- средняя степень приспособлености по всем примерам схемы
в популяции в момент времени
;
- Средняя приспособленность всей популяции -
;
-
- вероятность мутации;
-
- вероятность кроссинговера.
Теорема
Интерпретация теоремы
Пусть имеется какая-то начальная популяция. Рассмотрим некоторую схему небольшого порядка с небольшим определяющим расстоянием, степень приспособленности которой больше, чем в среднем по данной популяции. Тогда количество примеров этой схемы в последующих популяциях будет расти экспоненциально (конечно, не до бесконечности, но на протяжении некоторого числа популяций). Таким образом, "хорошие" в смысле приспособленности схемы (с дополнительными ограничениями на и
) сохраняются и покрывают все большую часть популяции. При этом дополнительные ограничения диктуются следующими соображениями: мутации реже разрушают схемы меньшего порядка, а кроссинговер реже разрушает схемы с меньшей определяющей длиной.
Гипотеза строительных блоков (building block hypothesis)
Была предложена Гольдбергом в 1989 году. Строительный блок - схема, обладающая следующими свойствами:
- Высокой приспособленностью
- Низким порядком
- Короткой определяющей длиной
Как показывает теорема схем, такие блоки экспоненциально увеличивают количество примеров по мере работы алгоритма. В связи с этим была высказана гипотеза, что "строительные блоки объединяются, чтобы сформировать лучшие блоки". Таким образом, рекомбинация и экспоненциальных рост примеров блоков ведет к формированию лучших блоков, которые в конечном итоге дадут решение (решение будет примером самой лучшей схемы-блока). Поэтому можно говорить о том, что ГА ведет поиск на множестве строительных блоков.
Критика
Гипотеза строительных блоков не является формальным математическим утверждением. Вот некоторые аргументы, опровергающие ее:
- Теорема схем описывает увеличение количества примеров только в следующем поколении. Далее может измениться приспособленность схемы и популяции, и увеличение может смениться уменьшением.
- Строго говоря, утверждение теоремы схем носит вероятностный характер (в левой части неравенства стоит математическое ожидание). Поэтому возможны отклонения от этого закона, а насколько они велики и вероятны - в теореме не указано.
- Комбинация двух "хороших" строительных блоков не всегда является "хорошей". Существуют примеры, когда такое комбинирование приводит к существенному снижению приспособленности схемы-блока.
Тем не менее, иногда гипотеза строительных блоков выполняется на практике. Далее следует пример.
Задача выбора признаков с помощью ГА
Предварительные замечания
Суть данной задачи ( см. Выбор признаков с помощью генетических алгоритмов (пример) ) позволяет предположить, что гипотеза строительных блоков выполняется. Действительно, схемы соответствуют наборам признаков. Тогда логично считать, что в большинстве случаев комбинация хороших наборов должна дать хороший набор.
Постановка вычислительного эксперимента
Данные порождались следующим образом (D - дисперсия, D=100):
x = [ 1:0.5:20 ]'; y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + sqrt( D ) * randn( size( x, 1 ), 1 );
Выборка делилась на training и testing части в соотношении 60%:40% случайным образом.
Использовался следующий набор порождающих функций (всего 12):
В наборе не было следующих функций, участвовавших в порождении:
Задача решалась простым ГА. При этом менялось значение параметра Размер Популяции.
Результаты
Выводы
Вероятно, гипотеза строительных блоков в данном случае выполняется.
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |