Статистический анализ данных (курс лекций, К.В.Воронцов)/2010

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м (→Задание 1. Исследование статистических критериев на модельных данных)
м
Строка 36: Строка 36:
[[Изображение:Answer3.jpg|500px]]
[[Изображение:Answer3.jpg|500px]]
 +
 +
[[Категория:Учебные курсы]]

Версия 18:58, 10 сентября 2010

Задание 1. Исследование статистических критериев на модельных данных

Необходимо провести исследование одного из классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо сгенерировать одну или несколько выборок из указанного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. При этом, в зависимости от индивидуальных особенностей задания, выборки могут как генерироваться заново для каждого значения объёма выборки n, так и образовываться путём добавления одного элемента к уже имеющейся выборке объёма n-1. По результатам расчётов необходимо построить указанные в задании графики, среди которых могут быть следующие:

  • график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
  • график зависимости достигаемого уровня значимости от значений параметров, усреднённого по нескольким десяткам экспериментов;
  • график с эмпирическими оценками мощности критерия для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся k раз для каждого набора значений параметра, и в m из k случаев гипотеза была отвергнута на некотором фиксированном уровне значимости \alpha (примем \alpha=0.05), оценкой мощности будет отношение m/k.

Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также *.m-файл.

Пример выполнения задания

Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига. x^n = (x_1,\ldots,x_n)\sim N(\mu_1,\sigma),\;\; y^n = (y_1,\ldots,y_n)\sim N(\mu_2,\sigma);

H_0\,:\; \mu_1=\mu_2,

H_1\,:\; \mu_1\neq\mu_2.

Параметры задачи принимают следующие значения:

\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.

При каждом значении \mu_2 выборки для разных значений n генерируются независимо.

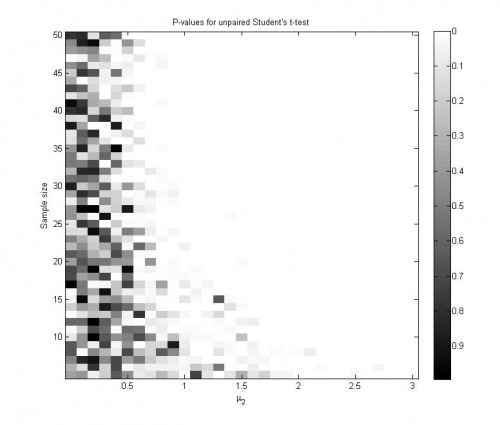
График значений достигаемого уровня значимости при однократной генерации выборок:

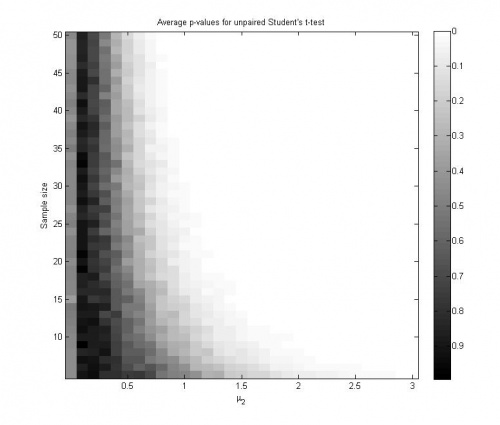
График значений достигаемого уровня значимости, усрёднённых по 100 экспериментам:

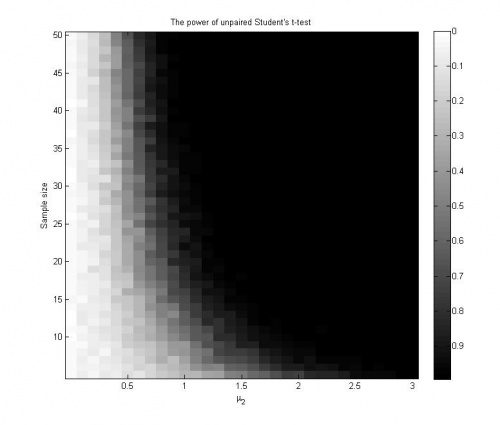
График значений эмпирических оценок мощности критерия при проведении 100 экспериментов (\alpha=0.05):

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2010»
Личные инструменты