Центральное множество

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(Новая: Начинайте писать здесь Категория:Медиальное представление формы)
 
(16 промежуточных версий не показаны.)
Строка 1: Строка 1:
-
Начинайте писать здесь
+
Центральное множество является математической формализацией понятия [[Скелет|скелета объекта]] для пространств произвольной размерности.
 +
== Определение ==
 +
Пусть <tex> \Omega </tex> --- связное открытое ограниченное подмножество <tex> \mathbb{R}^n </tex>.
 +
 
 +
Замкнутая шаровая окрестность <tex>B_r(x)\subseteq\overline{\Omega}</tex> точки <tex> x\in\overline{\Omega} </tex> называется '''максимальным шаром''' множества <tex>\Omega</tex>, если для любой точки <tex>y\in\Omega</tex> и любой ее замкнутой шаровой окрестности <tex>B_q(y)\subseteq\overline{\Omega}</tex> из того, что <tex>B_r(x)\subseteq B_q(y)</tex> следует, что <tex>B_r(x)=B_q(y)</tex>.
 +
 
 +
Максимальный шар множества <tex>\Omega</tex> также называется '''максимальным пустым шаром''' или '''максимальным вписанным шаром'''.
 +
 
 +
'''Центральным множеством''' ('''central set''') или '''[[Скелет|скелетом]]''' ('''skeleton''') <tex>\Omega</tex> называется множество <tex>S_{\Omega}</tex> центров пустых шаров <tex>\Omega</tex>.
 +
 
 +
== Пример ==
 +
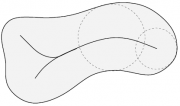
При <tex> n=2 </tex> центральное множество ([[Скелет|скелет]]) представляет собой множество центров максимальных пустых кругов [[плоская фигура|плоской фигуры]].
 +
[[Изображение:CentralSet2D.png|thumb|Центральное множество (скелет) плоской фигуры]]
 +
 
 +
== Связь между медиальным и центральным множествами ==
 +
Для любого связного открытого ограниченного множества <tex>\Omega\subset\mathbb{R}^n</tex> верно, что его [[Медиальное множество|медиальное множество]] <tex>M_{\Omega}</tex> является подмножеством его центрального множества: <tex> M_{\Omega}\subseteq S_{\Omega} </tex>.
 +
 
 +
При <tex> n=2 </tex>, <tex> M_{\Omega}=S_{\Omega} </tex>, если <tex>\Omega</tex> --- многоугольная фигура.
 +
 
 +
== См. также ==
 +
* [[Медиальное множество]]
 +
* [[Срединная ось]]
 +
* [[Скелет]]
 +
 
 +
==Литература==
 +
* Chazal F., Soufflet R. ''Stability and finiteness properties of Medial Axis and Skeleton'' // Journal of Dynamic and Control Systems, Vol. 10, No.2, 2004. pp. 149 -- 170. [http://www.maths.manchester.ac.uk/raag/preprints/0040.pdf]
 +
* Yomdin Y., ''On the local structure of a generic central set'' // Compositio Matematica, Vol. 43, No. 2, 1981, pp. 225 -- 238. [http://%5Bhttp://archive.numdam.org/ARCHIVE/CM/CM_1981__43_2/CM_1981__43_2_225_0/CM_1981__43_2_225_0.pdf]
[[Категория:Медиальное представление формы]]
[[Категория:Медиальное представление формы]]
 +
[[en|Central set]]

Текущая версия

Центральное множество является математической формализацией понятия скелета объекта для пространств произвольной размерности.

Содержание

Определение

Пусть \Omega --- связное открытое ограниченное подмножество \mathbb{R}^n .

Замкнутая шаровая окрестность B_r(x)\subseteq\overline{\Omega} точки x\in\overline{\Omega} называется максимальным шаром множества \Omega, если для любой точки y\in\Omega и любой ее замкнутой шаровой окрестности B_q(y)\subseteq\overline{\Omega} из того, что B_r(x)\subseteq B_q(y) следует, что B_r(x)=B_q(y).

Максимальный шар множества \Omega также называется максимальным пустым шаром или максимальным вписанным шаром.

Центральным множеством (central set) или скелетом (skeleton) \Omega называется множество S_{\Omega} центров пустых шаров \Omega.

Пример

При n=2 центральное множество (скелет) представляет собой множество центров максимальных пустых кругов плоской фигуры.

Центральное множество (скелет) плоской фигуры
Центральное множество (скелет) плоской фигуры

Связь между медиальным и центральным множествами

Для любого связного открытого ограниченного множества \Omega\subset\mathbb{R}^n верно, что его медиальное множество M_{\Omega} является подмножеством его центрального множества: M_{\Omega}\subseteq S_{\Omega} .

При n=2 , M_{\Omega}=S_{\Omega} , если \Omega --- многоугольная фигура.

См. также

Литература

  • Chazal F., Soufflet R. Stability and finiteness properties of Medial Axis and Skeleton // Journal of Dynamic and Control Systems, Vol. 10, No.2, 2004. pp. 149 -- 170. [1]
  • Yomdin Y., On the local structure of a generic central set // Compositio Matematica, Vol. 43, No. 2, 1981, pp. 225 -- 238. [2]Central set
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A6%D0%B5%D0%BD%D1%82%D1%80%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE»