Центральное множество

Материал из MachineLearning.

Версия 10:21, 15 мая 2011 (править) Иван Мехедов (Обсуждение | вклад) ← К предыдущему изменению		Текущая версия (10:33, 15 мая 2011) (править) (отменить) Иван Мехедов (Обсуждение | вклад)
(2 промежуточные версии не показаны)
Строка 28:		Строка 28:
	[[Категория:Медиальное представление формы]]		[[Категория:Медиальное представление формы]]
-		+	[[en|Central set]]
-	[[Central set]]	+

---

Текущая версия

Центральное множество является математической формализацией понятия скелета объекта для пространств произвольной размерности.

Содержание 1 Определение 2 Пример 3 Связь между медиальным и центральным множествами 4 См. также 5 Литература

Определение

Пусть --- связное открытое ограниченное подмножество .

Замкнутая шаровая окрестность точки называется максимальным шаром множества , если для любой точки и любой ее замкнутой шаровой окрестности из того, что следует, что .

Максимальный шар множества также называется максимальным пустым шаром или максимальным вписанным шаром.

Центральным множеством (central set) или скелетом (skeleton) называется множество центров пустых шаров .

Пример

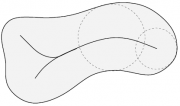
При центральное множество (скелет) представляет собой множество центров максимальных пустых кругов плоской фигуры.

Связь между медиальным и центральным множествами

Для любого связного открытого ограниченного множества верно, что его медиальное множество является подмножеством его центрального множества: .

При , , если --- многоугольная фигура.

См. также

• Медиальное множество
• Срединная ось
• Скелет

Литература

• Chazal F., Soufflet R. Stability and finiteness properties of Medial Axis and Skeleton // Journal of Dynamic and Control Systems, Vol. 10, No.2, 2004. pp. 149 -- 170. [1]
• Yomdin Y., On the local structure of a generic central set // Compositio Matematica, Vol. 43, No. 2, 1981, pp. 225 -- 238. [2]Central set