Суммаризация в анализе ДНК-микрочипов

Материал из MachineLearning.

(Различия между версиями)

Версия 08:38, 24 октября 2011

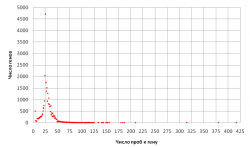
Распределение генов по числу проб к ним на микрочипе Affymetrix Human Gene 1.0 ST.

Суммаризация — этап предобработки при анализе ДНК-микрочипов, в ходе которого интенсивности флуоресценции проб, соответствующих одному гену, обобщаются в оценку его экспрессии.

Для обеспечения устойчивости оценки уровня экспрессии к каждому гену на микрочипе имеется несколько проб; их последовательности комплементарны разным участкам последовательности их гена.

Содержание

1 Одиночная суммаризация
2 Множественная суммаризация
- 2.1 fRMA (Frozen Robust Multi-Array Analysis)
  - 2.1.1 Обучение модели
  - 2.1.2 Обработка новых чипов
    - 2.1.2.1 Один микрочип
    - 2.1.2.2 Серия микрочипов
3 Примечания

Одиночная суммаризация

В данном классе методов оценки экспрессии вычисляются для всех микрочипов независимо друг от друга.

В комплексе методов предобработки MAS 5.0^[1] для суммаризации используется взвешенное среднее Тьюки, вычисленное одношаговым методом. Усреднение применяется к логарифмам интенсивностей флуоресценции проб и выполняется независимо для каждого гена на каждом микрочипе.

Множественная суммаризация

К данному классу методов относятся такие, которые для получения оценки экспрессии используют несколько микрочипов.

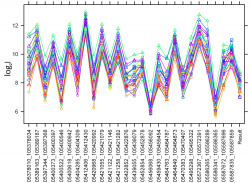
Интенсивности флуоресценции проб к одному и тому же гену в логарифмической шкале, каждая линия — один микрочип.

Интенсивности флуоресценции разных проб к одному и тому же гену могут отличаться на порядки, причём отличия между ними имеют в основном систематический характер. В комплексе методов предобработки RMA^[1] делается попытка учесть эти различия в рамках следующей модели:

$Y_{ijn}=\mu_{in}+\alpha_{jn}+\varepsilon_{ijn}.$

Здесь $Y_{ijn}$ — предобработанная (с вычтенным фоном и нормализованная) логирифмированная интенсивность флуоресценции пробы $j$ к гену $n$ на микрочипе $i$ , $\mu_{in}$ — оценка экспрессии гена $n$ на микрочипе $i$ в логарифмической шкале, $\alpha_{jn}$ — коэффициент аффинитивности $j$ -й пробы $n$ -му гену, $\varepsilon_{ijn}$ — случайная ошибка с нулевым средним. Для однозначности определения параметров предполагается дополнительно $\sum_j \alpha_j=0$ для каждого гена.

В RMA значения коэффициентов оцениваются при помощи алгоритма median polish^[1].

fRMA (Frozen Robust Multi-Array Analysis)

Рассматривается следующая модель уровня экспрессии^[1]:

(1)

$Y_{ijkn} = \theta_{in} + \phi_{jn} + \gamma_{jkn} + \varepsilon_{ijkn}$

Здесь используются следующие обозначения:

$k$ — номер серии микрочипов $k \in 1, \dots, K$ . Два чипа относятся к одной серии, если эксперименты с ними были проведены в одной лаборатории в одно и то же время.
$i$ — номер микрочипа $i \in 1, \dots, I_k$ .
$n$ — номер набора проб $n \in 1, \dots, N$ . Также через $n$ обозначается номер гена, соответствующего $n$ -му набору проб.
$j$ — номер пробы $i \in 1, \dots, J_n$ .
$Y_{ijkn}$ — предобработанная (с вычтенным фоном и нормализованная) логарифмированная интенсивность пробы $j$ из набора проб $n$ микрочипа $i$ из партии микрочипов $k$ .
$\theta_{in}$ — экспрессия гена $n$ на $i$ -м микрочипе.
$\phi_{jn}$ — коэффициент сродства пробы $j$ гену $n$ .
$\gamma_{jkn}$ — случайная ошибка, вызывающая различия между партиями проб.
$\varepsilon_{ijkn}$ — случайная ошибка, вызывающая различия между пробами на чипах одной партии.

В данной модели предполагается, что пробы на разных чипах имеют одинаковую дисперсию случайной ошибки: $\mathbb{D} \varepsilon_{ijkn} = \sigma_{jn}^2$ . Также делается предположение, что $\gamma_{jkn}$ — это случайная величина, дисперсия которой не зависит от серии чипов: $\mathbb{D} \gamma_{jkn} = \tau_{jn}^2$ .

Обучение модели

Для обучения необходимы данные с большого числа микрочипов.

Сначала ко всем микрочипам применяется метод квантильной нормализации, приводящий все данные к одному распределению. В дальнейшем будем называть это распределение «представительным».

Непосредственная настройка модели (1) при наличии выбросов в обучающей выборке крайне сложна, поэтому предлагается перейти к более простой задаче. Рассматривается упрощенная модель

$Y_{ijn} = \theta_{in} + \phi_{jn} + \varepsilon_{ijn}$ .

По обучающей выборке находятся робастные оценки параметров $\hat \theta_{in}$ и $\hat \phi_{jn}$ для данной модели. Затем вычисляются остатки $r_{ijkn} = Y_{ijkn} - \left( \hat \theta_{in} + \hat \phi_{jn} \right)$ , с помощью которых оцениваются дисперсии $\sigma_{jn}^2$ и $\tau_{jn}^n$ :

$\hat \tau_{jn}^2 = \frac{1}{K} \sum_{k = 1}^{K} \left( \bar r_{.jkn} - \bar r_{.j.n} \right)^2$ ;

$\hat \sigma_{jn}^2 = \frac{1}{K} \sum_{k = 1}^{K} \frac{1}{I_k} \sum_{i = 1}^{I_k} \left( r_{ijkn} - \bar r_{.jkn} \right)^2$ ,

где $\bar r_{.jkn} = \frac{1}{I_k} \sum_{i = 1}^{I_k} r_{ijkn},\; \bar r_{.j.n} = \frac{1}{K} \sum_{k = 1}^{K} \frac{1}{I_k} \sum_{i = 1}^{I_k} r_{ijkn}$ .

Обработка новых чипов

Рассмотрим процесс обработки новых чипов. Сначала делается фоновая поправка всех чипов методом RMA-свертки, затем с помощью квантильной нормализации интенсивности новых чипов приводятся к представительному распределению, полученному на этапе обучения. Последним шагом является суммаризация, которая подробно описана ниже.

В первую очередь делается поправка интенсивностей проб для учета коэффициента сродства:

(2)

$Y_{ijln}^* = Y_{ijln} - \hat \phi_{jn} \approx \theta_{in} + \gamma_{jln} + \varepsilon_{ijln}$

(здесь $l$ — это индекс новой партии микрочипов).

Далее из скорректированных интенсивностей нужно получить робастную оценку для $\theta$ . Это делается разными способами в зависимости от того, из скольких чипов состоит серия.

Один микрочип

В данном случае индексы $i$ и $l$ могут быть опущены опущены, так как обрабатывается один микрочип и одна серия.

Логарифмированная концентрация оценивается следующим образом:

$\hat \theta_n = \frac{\sum_{j = 1}^{J_n} \frac{w_{jn}}{v_{jn}} Y_{jn}^*}{\sum_{j = 1}^{J_n} \frac{w_{jn}}{v_{jn}}}$ ,

где $v_{jn} = \hat \tau_{jn}^2 + \hat \sigma_{jn}^2$ — оценка дисперсии скорректированной интенсивности $Y_{jn}^*$ , а $w_{jn}$ — веса, соответствующие некоторой M-оценке.

Данная оценка учитывает с низкими весами выбросы (так как им соответствуют маленькие $w_{jn}$ ) и пробы с большой дисперсией шума.

Серия микрочипов

В данном случае индекс $l$ может быть опущен, так как обрабатывается одна серия микрочипов. Число чипов в новой серии будем обозначать через $I$

Введем следующие обозначения:

${\mathbf X} = 1_{J_n \times 1} \otimes \mathbf{E}_{I \times I}$ — индикаторная матрица ( $1_{m \times n}$ — матрица из единиц размера $m \times n$ ; ${\mathbf E}_{n \times n}$ — единичная матрица размера $n \times n$ ; $\otimes$ — произведение Кронекера).
${\mathbf \theta} = \left( \theta_{1 n}, \dots, \theta_{I n} \right)$ — вектор экспрессий.
${\mathbf Y_{jn}^*} = \left( Y_{ijn}^* \right)_{i = 1}^{I} \in \mathbb{R}^I$ — вектор интенсивностей пробы $j$ набора $n$ на всех чипах партии.
${\mathbf Y_n^*} = \left( {\mathbf Y_{1,n}^*, \dots, Y_{J_n, n}^* } \right)^T \in \mathbb{R}^{I J_n}$ — вектор интенсивностей всех проб к гену $n$ на всех чипах партии.
${\mathbf \delta} \in \mathbb{R}^{I J_n}$ — вектор случайных ошибок, соответствующих интенсивностям из ${\mathbf Y_n^*}$ .

Тогда модель (2) можно записать в матричном виде:

$\mathbf Y_n^* = X \theta + \delta$

Матрица ковариации вектора случайных ошибок $\mathbf \delta$ задается следующим образом:

${\mathbf \delta}_{i_1 j_1, i_2 j_2} = cov \left( Y_{i_1 j_1 n}^*,\; Y_{i_2 j_2 n}^* \right) = \begin{cases} \tau_{jn}^2 + \sigma_{jn}^2, & \text{if } j_1 = j_2 = j, \; i_1 = i_2, \\ \tau_{jn}^2, & \text{if } j_1 = j_2 = j, \; i_1 \neq i_2, \\ 0, & \text{otherwise} \end{cases}$

С учетом данного выражения ковариационную матрицу вектора $\mathbf \delta$ можно записать следующим образом:

${\mathbf \Sigma} = diag \left( \tau_{1n}^2, \dots, \tau_{J_n, n}^2 \right) \otimes 1_{I \times I} + diag \left( \sigma_{1n}^2, \dots, \sigma_{J_n, n}^2 \right) \otimes {\mathbf E}_{I \times I}$

Для параметров $\tau_{jn}^2$ И $\sigma_{jn}^2$ уже получены оценки, поэтому матрицу $\mathbf \Sigma$ можно считать известной. Значит, с помощью преобразования $\mathbf Z_n^* = \Sigma^{-\frac{1}{2}} Y_n^*$ можно добиться независимости случайных ошибок. Тогда робастную оценку для $\mathbf \theta$ можно получить из следующей задачи взвешенных наименьших квадратов:

$\left\| {\mathbf W \left( \Sigma^{-\frac{1}{2}} Y_n^* - \Sigma^{-\frac{1}{2}} X \theta \right) } \right\|^2 \rightarrow \min_{\mathbf \theta}$ ,

где $\mathbf W$ — диагональная матрица весов, соответствующих некоторой M-оценке.

Решение записывается следующим образом:

${\mathbf \hat \theta} = \left( {\mathbf X^T \Sigma^{-\frac{1}{2}} W \Sigma^{-\frac{1}{2}} X} \right)^{-1} {\mathbf X^T \Sigma^{-\frac{1}{2}} W \Sigma^{-\frac{1}{2}} Y_n^* }$ .

Примечания

Это незавершённая статья. Вы поможете проекту, исправив и дополнив её.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%83%D0%BC%D0%BC%D0%B0%D1%80%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F_%D0%B2_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B5_%D0%94%D0%9D%D0%9A-%D0%BC%D0%B8%D0%BA%D1%80%D0%BE%D1%87%D0%B8%D0%BF%D0%BE%D0%B2»

Категории: Биоинформатика | Незавершённые статьи

@@ Строка 30: / Строка 30: @@
 Здесь используются следующие обозначения:
-* <tex>k</tex> — номер партии микрочипов <tex> k \in 1, \dots, K </tex>. Два чипа относятся к одной партии, если эксперименты с ними были проведены в одной лаборатории в одно и то же время.
+* <tex>k</tex> — номер серии микрочипов <tex> k \in 1, \dots, K </tex>. Два чипа относятся к одной серии, если эксперименты с ними были проведены в одной лаборатории в одно и то же время.
 * <tex>i</tex> — номер микрочипа <tex> i \in 1, \dots, I_k </tex>.
-* <tex>n</tex> — номер набора проб <tex> n \in 1, \dots, N </tex>. Также через <tex>n</tex>  мы будем обозначать номер гена, соответствующего <tex>n</tex>-му набору проб.
+* <tex>n</tex> — номер набора проб <tex> n \in 1, \dots, N </tex>. Также через <tex>n</tex> обозначается номер гена, соответствующего <tex>n</tex>-му набору проб.
 * <tex>j</tex> — номер пробы <tex> i \in 1, \dots, J_n </tex>.
 * <tex>Y_{ijkn}</tex> — предобработанная (с вычтенным фоном и нормализованная) логарифмированная интенсивность пробы <tex>j</tex> из набора проб <tex>n</tex> микрочипа <tex>i</tex> из партии микрочипов <tex>k</tex>.
@@ Строка 41: / Строка 41: @@
 В данной модели предполагается, что пробы на разных чипах имеют одинаковую дисперсию случайной ошибки: <tex>\mathbb{D} \varepsilon_{ijkn} = \sigma_{jn}^2</tex>.
-Также делается предположение, что <tex>\gamma_{jkn}</tex> — это случайная величина, дисперсия которой не зависит от партии чипов: <tex>\mathbb{D} \gamma_{jkn} = \tau_{jn}^2</tex>.
+Также делается предположение, что <tex>\gamma_{jkn}</tex> — это случайная величина, дисперсия которой не зависит от серии чипов: <tex>\mathbb{D} \gamma_{jkn} = \tau_{jn}^2</tex>.
 ==== Обучение модели ====
@@ Строка 73: / Строка 73: @@
 Далее из скорректированных интенсивностей нужно получить робастную оценку для <tex>\theta</tex>.
-Это делается разными способами в зависимости от того, из скольких чипов состоит партия.
+Это делается разными способами в зависимости от того, из скольких чипов состоит серия.
 ===== Один микрочип =====
-В данном случае индексы <tex>i</tex> и <tex>l</tex> могут быть опущены опущены, так как обрабатывается один микрочип и одна партия.
+В данном случае индексы <tex>i</tex> и <tex>l</tex> могут быть опущены опущены, так как обрабатывается один микрочип и одна серия.
 Логарифмированная концентрация оценивается следующим образом:
@@ Строка 85: / Строка 85: @@
 Данная оценка учитывает с низкими весами выбросы (так как им соответствуют маленькие <tex>w_{jn}</tex>) и пробы с большой дисперсией шума.
-===== Партия микрочипов =====
+===== Серия микрочипов =====
-В данном случае индекс <tex>l</tex> может быть опущен, так как обрабатывается одна партия микрочипов. Число чипов в новой партии будем обозначать через <tex>I</tex>
+В данном случае индекс <tex>l</tex> может быть опущен, так как обрабатывается одна серия микрочипов. Число чипов в новой серии будем обозначать через <tex>I</tex>
 Введем следующие обозначения: