Использование метода Белсли для прореживания признаков

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Содержание

1 Постановка задачи
2 Описание алгоритма
- 2.1 Методика Belsley, Kuh, и Welsch (BKW)
3 Вычислительный эксперимент
- 3.1 Пример 1
- 3.2 Пример 2
4 Исходный код
5 Смотри также
6 Литература

Постановка задачи

Задана выборка $D = \{ y_i,\mathbf{x}_i\}_{i=1}^n$ признаков и зависимой переменной. Рассматривается линейная регрессионная модель вида:

$y_i=\sum_{j=1}^m b_j x_{ij} + \varepsilon_i, i=1,\dots,n$ Предполагается, что вектор регрессионных невязок имеет нулевое математическое ожидание и дисперсию $\sigma^2$ . С помощью метода Белсли требуется выявить мультиколлинеарность признаков и устранить её.

Описание алгоритма

Методика Belsley, Kuh, и Welsch (BKW)

Согласно Белсли для выделения мультиколлинеарных зависимостей с матрицей $X$ производят сингулярное разложение

$X=UDV^T,$

${U}^{T}U={V}^{T}V={I}_{p}$
$D$ - диагональная с неотрицательными элементами ${\lambda}_{1},...,{\lambda}_{p}$ называющимися сингулярными числами $X$ . Далее вычисляются два параметра, по которым будет будет определяться зависимость
1) Индексы обусловленности это: ${\eta}_{k}\equiv\frac{{\lambda}_{max}}{{\lambda}_{k}}$ , $k=1,...,p$ .
Наибольший из индексов обусловленности -- это число обусловленности матрицы $X$ . Большое значение ${\eta}_{k}$ указывает на зависимость близкую к линейной между признаками и чем больше ${\eta}_{k}$ тем сильнее зависимость.
2) Дисперсионные доли.
Дисперсионные доли находятся следующим образом: из сингулярного разложения ковариационная матрица метода наименьших квадратов может быть записана как:
$V(b)={\sigma}^{2}(X^{T}X)^{-1} = {\sigma}^{2}V D^{-2} V^{T}$
Таким образом дисперсия $k$ -го регрессионного коэффициента ${b}_{k}$ это $k$ -й диагональный элемент $V(b)$

$\mbox{var}({b}_{k})={\sigma}^{2} \sum_{j} {\frac{{\upsilon}^{2}_{kj}}{{\lambda}^{2}_{j}}}$

где $V=({\upsilon}_{ij})$ .
Определим $k, j$ -е дисперсионное соотношение как долю дисперсии $k$ -го регрессионного коэффициента связанная с $j$ -м компонентом его разложения. Доля считается как:
${\phi}_{kj}\equiv\frac{{\upsilon}^{2}_{kj}}{{\lambda}^{2}_{j}}$ , ${\phi}_{k}\equiv\sum^{p}_{j=1} {\phi}_{kj}$ , $k=1,...,p$
Дисперсионное соотношение:
${\pi}_{jk}\equiv\frac{{\phi}_{kj}}{{\phi}_{k}}$ , $k,j=1,...,p$
Наличие мультиколлинеарности определяется по таблице.

Индекс обусловленности	$var({b}_{1})$	$var({b}_{2})$	$...$	$var({b}_{p})$
${\eta}_{1}$	${\pi}_{11}$	${\pi}_{21}$	...	${\pi}_{p1}$
${\eta}_{2}$	${\pi}_{12}$	${\pi}_{22}$	...	${\pi}_{p2}$
$\vdots$	$\vdots$	$\vdots$		$\vdots$
${\eta}_{p}$	${\pi}_{1p}$	${\pi}_{2p}$	...	${\pi}_{pp}$

Большие величины ${\eta}_{i}$ означают, чтовозможно есть зависимость между признаками.
Большие значения ${\pi}_{ij}$ в соответствующих строках относятся к признакам, между которыми эта зависимость существует.

Вычислительный эксперимент

Пример 1

В эксперименте используются модельные данные, для которых вычисляется матрица Belsley в зависимоти от параметра определяющего степень коллинеарности между признаками. Используются два ортогональных признака $x_1$ , $y_2$ и третий признак $y_1$ зависящий от параметра $k$ . При $k=0$ все признаки ортогональны, при увеличении $k$ зависимый признак $y_1$ приближается к $x_1$ , вплоть до полной коллинеарности при $k=1$ . Зависимость индексов обусловленности ${\eta}_{i}$ от $k$ :

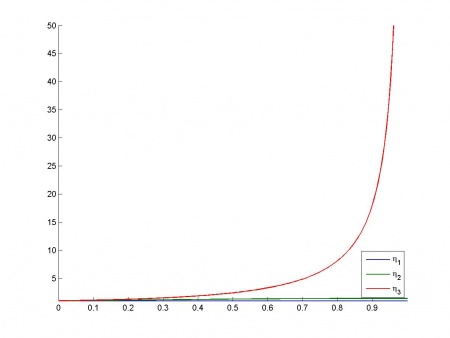
Пример 2

Используются реальные данные по продажам товаров. Для двух различных матриц $X$ был проведён эксперимент по вычислению таблицы BKW

1)

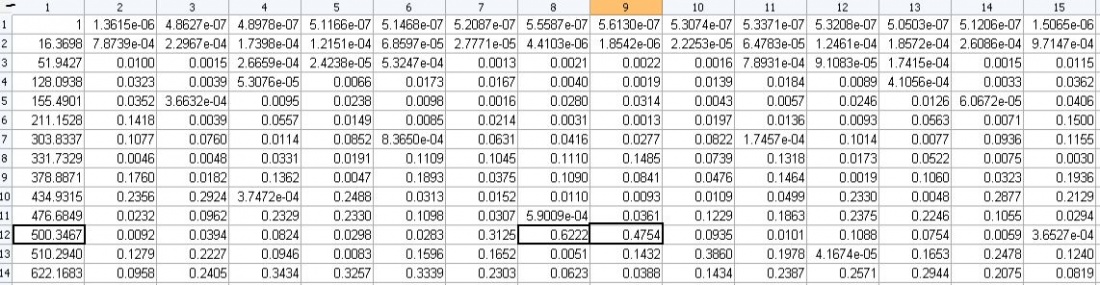
Из таблицы видно, что наблюдается связь между признаками 8 и 9

2)

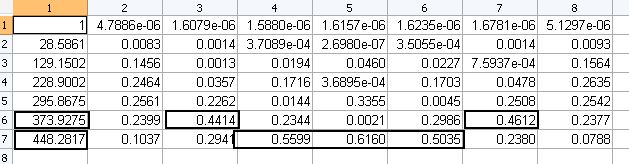
Самому большому индексу обусловленности соответствует связь между 4,5 и 6-ым признаками, также наблюдается связь между признаками 3 и 7.

Исходный код

Смотри также

Литература

В.В. Стрижов Методы выбора регрессионных моделей
Gianfranco Galmacci, Collinearity Detection in Linear Regression. Computational Economics 9:215-227, 1996.

Данная статья была создана в рамках учебного задания.

Студент: Литвинов Игорь

Преподаватель: В.В.Стрижов

Срок: осень 2011

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%98%D1%81%D0%BF%D0%BE%D0%BB%D1%8C%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%B0_%D0%91%D0%B5%D0%BB%D1%81%D0%BB%D0%B8_%D0%B4%D0%BB%D1%8F_%D0%BF%D1%80%D0%BE%D1%80%D0%B5%D0%B6%D0%B8%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%D0%BF%D1%80%D0%B8%D0%B7%D0%BD%D0%B0%D0%BA%D0%BE%D0%B2»

Категории: Практика и вычислительные эксперименты | Линейная регрессия

@@ Строка 55: / Строка 55: @@
 Используются два ортогональных признака <tex>x_1</tex>, <tex>y_2</tex> и третий признак <tex>y_1</tex> зависящий от параметра <tex>k</tex>. При <tex>k=0</tex> все признаки ортогональны, при увеличении <tex>k</tex> зависимый признак <tex>y_1</tex> приближается к <tex>x_1</tex>, вплоть до полной коллинеарности при <tex>k=1</tex>.
 Зависимость индексов обусловленности <tex>{\eta}_{i}</tex> от <tex>k</tex>:<br/>
+[[Изображение:plot3sci.jpg|450px]]<br/>
 ===Пример 2===
-Используются реальные данные
+Используются реальные данные по продажам товаров.
+Для двух различных матриц <tex>X</tex> был проведён эксперимент по вычислению таблицы BKW <br/><br/>
+)
+[[Изображение:plotfirst.jpg|1100px]]<br/><br/>
+Из таблицы видно, что наблюдается связь между признаками 8 и 9<br/>
+)
+[[Изображение:plotsecond.jpg|1100px]]<br/><br/>
+Самому большому индексу обусловленности соответствует связь между 4,5 и 6-ым признаками, также наблюдается связь между признаками 3 и 7.
+== Исходный код ==
+== Смотри также ==
+* [[Мультиколлинеарность]]
+* [[Метод наименьших квадратов]]
+* [[Линейная регрессия (пример)]]
+* [[Анализ мультиколлинеарности (пример)]]
+* [[Сингулярное разложение]]
+* [[Метод Белсли]]
+== Литература ==
+* В.В. Стрижов Методы выбора регрессионных моделей
+* Gianfranco Galmacci, Collinearity Detection in Linear Regression. Computational Economics 9:215-227, 1996.
+{{ЗаданиеВыполнено|Литвинов Игорь|В.В.Стрижов|осень 2011|e1ekt|strijov}}
+[[Категория:Практика и вычислительные эксперименты]]
+[[Категория:Линейная регрессия]]