Множественная проверка гипотез
Материал из MachineLearning.
м |
м (→Меры ошибки первого рода при множественной проверке) |
||
| (14 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
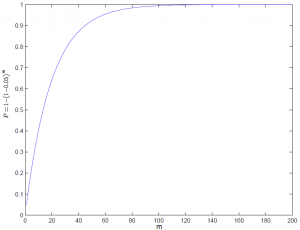
[[Изображение:Fwer.PNG|thumb|300px|Зависимость вероятности наличия ложных отклонений от мощности семейства гипотез.]] | [[Изображение:Fwer.PNG|thumb|300px|Зависимость вероятности наличия ложных отклонений от мощности семейства гипотез.]] | ||
| - | '''Множественная проверка гипотез''' — класс задач [[Математическая статистика|прикладной статистики]], возникающий при необходимости одновременного построения семейства статистических выводов. В каждое такое утверждение, представляющее собой вывод об отвержении гипотезы при [[Проверка статистических гипотез|проверке статистических гипотез]], изначально закладывается возможность ошибки ([[Проверка статистических гипотез#Ошибки первого и второго рода| | + | '''Множественная проверка гипотез''' — класс задач [[Математическая статистика|прикладной статистики]], возникающий при необходимости одновременного построения семейства статистических выводов. В каждое такое утверждение, представляющее собой вывод об отвержении гипотезы при [[Проверка статистических гипотез|проверке статистических гипотез]], изначально закладывается возможность ошибки (ложного отклонения гипотезы, [[Проверка статистических гипотез#Ошибки первого и второго рода|ошибки первого рода]]). Вероятность такой ошибки ограничивается неким достаточно малым значением — уровнем значимости <tex>\alpha</tex> (например, часто берут <tex>\alpha=0.05</tex>), выражающим степень неуверенности в справедливости заключения. При одновременном построении <tex>m</tex> заключений это приводит к тому, что вероятность совершения хотя бы одной такой ошибки оказывается ограничена сверху величиной вида <tex>1-(1-\alpha)^m</tex>, которая является недопустимо большой уже для достаточно малых <tex>m</tex>, то есть, с достаточно большой вероятностью рассматриваемое множество выводов содержит ошибочные. Для устранения этого эффекта, называемого '''эффектом множественных сравнений''', разработан ряд статистических техник. Процедура принятия или отклонения гипотез перестраивается таким образом, чтобы некая величина, являющаяся многомерным обобщением ошибки первого рода, была ограничена сверху наперёд заданным числом. |
==Примеры== | ==Примеры== | ||
| - | * В 1950 году Джозеф Райн проводил эксперименты по выявлению людей с экстрасенсорными способностями. Каждый испытуемый должен был угадать цвет каждой карты в последовательности из 10 карт. В таком опыте вероятность случайно угадать 9 или 10 карт из 10 составляет 11*2<sup>-10</sup> ≈ 0.01 — достаточно редкое событие, чтобы признать его маловероятным, поэтому Райн считал его свидетельством того, что испытуемый — экстрасенс. Однако, поскольку в опыте участвовало 1000 человек, вероятность того, что хотя бы один из них случайно угадает 9 или 10 карт составляла 1-(1-11*2<sup>-10</sup>)<sup>1000</sup> ≈ 0.9998. Действительно, из 1000 испытуемых 12 человек угадали 9 из 10 карт, двое все 10 карт. В последующих экспериментах ни один из них не подтвердил свои способности. | + | * В 1950 году Джозеф Райн проводил эксперименты по выявлению людей с экстрасенсорными способностями. Каждый испытуемый должен был угадать цвет каждой карты в последовательности из 10 карт. В таком опыте вероятность случайно угадать 9 или 10 карт из 10 составляет 11*2<sup>-10</sup> ≈ 0.01 — достаточно редкое событие, чтобы признать его маловероятным, поэтому Райн считал его свидетельством того, что испытуемый — экстрасенс. Однако, поскольку в опыте участвовало 1000 человек, вероятность того, что хотя бы один из них случайно угадает 9 или 10 карт составляла 1-(1-11*2<sup>-10</sup>)<sup>1000</sup> ≈ 0.9998. Действительно, из 1000 испытуемых 12 человек угадали 9 из 10 карт, двое — все 10 карт. В последующих экспериментах ни один из них не подтвердил свои способности. |
* Пусть инвестор выбирает, в какие из множества инвестиционных фондов вложить свои деньги. Для оценки инвестиционной привлекательности каждого фонда он вынужден использовать статистический критерий, чтобы отделить фонды, получившие в прошлом прибыль за счёт правильной стратегии управления, от тех, которые получили прибыль только в силу влияния случайных факторов. Чем больше множество фондов, из которых инвестор выбирает, тем больше вероятность того, что какие-то из них покажутся ему потенциально прибыльными, даже если их успех имел не систематический характер. | * Пусть инвестор выбирает, в какие из множества инвестиционных фондов вложить свои деньги. Для оценки инвестиционной привлекательности каждого фонда он вынужден использовать статистический критерий, чтобы отделить фонды, получившие в прошлом прибыль за счёт правильной стратегии управления, от тех, которые получили прибыль только в силу влияния случайных факторов. Чем больше множество фондов, из которых инвестор выбирает, тем больше вероятность того, что какие-то из них покажутся ему потенциально прибыльными, даже если их успех имел не систематический характер. | ||
| Строка 12: | Строка 12: | ||
== Обозначения == | == Обозначения == | ||
| - | Пусть <tex>H = \{H_1,\ldots, | + | Пусть <tex>H = \{H_1,\ldots,H_m\}</tex> — множество нулевых гипотез, проверяемых против альтернатив общего вида <tex>H'_{i} = \bar{H}_i, \: i=1,\ldots,m.</tex> Если нулевая гипотеза верна, будем писать <tex>H_i=0,</tex> и <tex>H_i=1</tex> в противном случае. |
| - | Пусть <tex> | + | За <tex>p =\{p_1,\ldots,p_m\}</tex> обозначим множество [[Достигаемый уровень значимости|пи-величин]], полученных при проверке соответствующих гипотез <tex>H_i</tex> подходящими статистическими критериями. |
| + | |||
| + | Пусть <tex>M_0=\{i:\:H_i=0\}</tex> и <tex>M_1=\{i:\:H_i=1\}</tex> — неизвестные множества индексов верных и неверных нулевых гипотез, <tex>m_0=\left|M_0\right|,</tex> <tex>m_1=\left|M_1\right|,</tex> <tex>\left|M_0\cup M_1\right|=m.</tex> Количество отклонённых нулевых гипотез <tex>R</tex> и количество принятых <tex>W = m-R</tex> — наблюдаемые случайные величины, в то время как величины <tex>S,\;T,\;U</tex> и <tex>V</tex> из приведённой ниже таблицы являются ненаблюдаемыми. | ||
<center> | <center> | ||
{| class = "standard" | {| class = "standard" | ||
| Строка 25: | Строка 27: | ||
! style="background: white" | <tex>U</tex> | ! style="background: white" | <tex>U</tex> | ||
! style="background: white" | <tex>V</tex> | ! style="background: white" | <tex>V</tex> | ||
| - | ! style="background: white" | <tex> | + | ! style="background: white" | <tex>m_0</tex> |
|- | |- | ||
! |Число неверных<br />гипотез | ! |Число неверных<br />гипотез | ||
! style="background: white" | <tex>T</tex> | ! style="background: white" | <tex>T</tex> | ||
! style="background: white" | <tex>S</tex> | ! style="background: white" | <tex>S</tex> | ||
| - | ! style="background: white" | <tex> | + | ! style="background: white" | <tex>m_1</tex> |
|- | |- | ||
! |Всего | ! |Всего | ||
! style="background: white" | <tex>W</tex> | ! style="background: white" | <tex>W</tex> | ||
! style="background: white" | <tex>R</tex> | ! style="background: white" | <tex>R</tex> | ||
| - | ! style="background: white" | <tex> | + | ! style="background: white" | <tex>m</tex> |
|} | |} | ||
</center> | </center> | ||
| + | Задача состоит в том, чтобы выбрать метод, допускающий минимальное число ложных отклонений гипотез <tex>V</tex> и ложных принятий <tex>T.</tex> Как и в одномерном случае, подход заключается в том, чтобы, ограничив меру ошибки первого рода малой величиной <tex>\alpha,</tex> выбрать процедуру, минимизирующую меру ошибки второго рода, т.е., максимизирующую [[Проверка статистических гипотез#Свойства статистических критериев|мощность]]. | ||
== Типы семейств гипотез == | == Типы семейств гипотез == | ||
| Строка 43: | Строка 46: | ||
== Меры ошибки первого рода при множественной проверке == | == Меры ошибки первого рода при множественной проверке == | ||
| - | + | Существует большое количество величин, обобщающих определение ошибки первого рода на задачу множественной проверки гипотез. Наиболее популярны следующие: | |
| - | == | + | * [[FWER]] — familywise error rate, групповая вероятность ошибки (первого рода): <tex>\operator{FWER}=\operator{P}\left(V\geq 1\right);</tex> |
| + | * [[k-FWER|k-FWER, gFWER]] — generalized familywise error rate, обобщённая групповая вероятность ошибки (первого рода): <tex>\operator{k-FWER}=\operator{P}\left(V\geq k\right);</tex> | ||
| + | * [[FDP]] — false discovery proportion, доля ложных отклонений гипотез (среди всех отклонений): <tex>\operator{FDP}=\left\{ \begin{array}{ll}\frac{V}{R}, & R>0, \\ 0, & R=0; \end{array}\right.</tex> | ||
| + | * [[FDR]] — false discovery rate, средняя доля ложных отклонений гипотез (среди всех отклонений): <tex>\operator{FDR}= \mathrm{E}\!\left[ \operator{FDP}\right ].</tex> | ||
| + | === Связь между мерами ошибки первого рода === | ||
| + | * <tex>\frac{\mathrm{E\left[V\right]}}{m}\leq\operator{FDR}\leq\operator{FWER}\leq\mathrm{E\left[V\right].</tex> | ||
| + | * При <tex>m=m_0</tex> (все рассматриваемые гипотезы верны) <tex>\operator{FWER}=\operator{FDR}.</tex> | ||
== Литература == | == Литература == | ||
| + | # E. L. Lehmann, J. P. Romano: Testing statistical hypotheses. Springer, New York, 2005 (3rd edition), 786 pages. Chapter 9: Multiple testing and simultaneous inference. | ||
== Ссылки == | == Ссылки == | ||
| - | * [http://en.wikipedia.org/wiki/Multiple_comparisons Multiple comparisons] — статья из английской Википедии | + | * [http://en.wikipedia.org/wiki/Multiple_comparisons Multiple comparisons] — статья из английской Википедии. |
== Примечания == | == Примечания == | ||
[[Категория:Прикладная статистика]] | [[Категория:Прикладная статистика]] | ||
| + | [[Категория:Множественная проверка гипотез]] | ||
| + | |||
{{Stub}} | {{Stub}} | ||
Текущая версия
Множественная проверка гипотез — класс задач прикладной статистики, возникающий при необходимости одновременного построения семейства статистических выводов. В каждое такое утверждение, представляющее собой вывод об отвержении гипотезы при проверке статистических гипотез, изначально закладывается возможность ошибки (ложного отклонения гипотезы, ошибки первого рода). Вероятность такой ошибки ограничивается неким достаточно малым значением — уровнем значимости (например, часто берут
), выражающим степень неуверенности в справедливости заключения. При одновременном построении
заключений это приводит к тому, что вероятность совершения хотя бы одной такой ошибки оказывается ограничена сверху величиной вида
, которая является недопустимо большой уже для достаточно малых
, то есть, с достаточно большой вероятностью рассматриваемое множество выводов содержит ошибочные. Для устранения этого эффекта, называемого эффектом множественных сравнений, разработан ряд статистических техник. Процедура принятия или отклонения гипотез перестраивается таким образом, чтобы некая величина, являющаяся многомерным обобщением ошибки первого рода, была ограничена сверху наперёд заданным числом.
Содержание |
Примеры
- В 1950 году Джозеф Райн проводил эксперименты по выявлению людей с экстрасенсорными способностями. Каждый испытуемый должен был угадать цвет каждой карты в последовательности из 10 карт. В таком опыте вероятность случайно угадать 9 или 10 карт из 10 составляет 11*2-10 ≈ 0.01 — достаточно редкое событие, чтобы признать его маловероятным, поэтому Райн считал его свидетельством того, что испытуемый — экстрасенс. Однако, поскольку в опыте участвовало 1000 человек, вероятность того, что хотя бы один из них случайно угадает 9 или 10 карт составляла 1-(1-11*2-10)1000 ≈ 0.9998. Действительно, из 1000 испытуемых 12 человек угадали 9 из 10 карт, двое — все 10 карт. В последующих экспериментах ни один из них не подтвердил свои способности.
- Пусть инвестор выбирает, в какие из множества инвестиционных фондов вложить свои деньги. Для оценки инвестиционной привлекательности каждого фонда он вынужден использовать статистический критерий, чтобы отделить фонды, получившие в прошлом прибыль за счёт правильной стратегии управления, от тех, которые получили прибыль только в силу влияния случайных факторов. Чем больше множество фондов, из которых инвестор выбирает, тем больше вероятность того, что какие-то из них покажутся ему потенциально прибыльными, даже если их успех имел не систематический характер.
- Пусть сравниваются способности нового и уже существующего лекарств влиять на ряд симптомов некоторого заболевания, причём, поскольку интерес представляют выводы отдельно по каждому симптому, проверяются покомпонентные гипотезы превосходства нового лекарства над старым. Чем больше список рассматриваемых симптомов, тем более вероятно, что новый препарат окажется лучше старого хотя бы в отношении одного из симптомов.
- Пусть проверяется безопасность нового лекарства путём проверки наличия большого количества побочных эффектов. Чем больше побочных эффектов рассматривается, тем более вероятно, что хотя бы один из них будет признан связанным с употреблением лекарства.
Обозначения
Пусть — множество нулевых гипотез, проверяемых против альтернатив общего вида
Если нулевая гипотеза верна, будем писать
и
в противном случае.
За обозначим множество пи-величин, полученных при проверке соответствующих гипотез
подходящими статистическими критериями.
Пусть и
— неизвестные множества индексов верных и неверных нулевых гипотез,
Количество отклонённых нулевых гипотез
и количество принятых
— наблюдаемые случайные величины, в то время как величины
и
из приведённой ниже таблицы являются ненаблюдаемыми.
| Число принятых гипотез | Число отвергнутых гипотез | Всего | |
|---|---|---|---|
| Число верных гипотез | | | |
| Число неверных гипотез | | | |
| Всего | | | |
Задача состоит в том, чтобы выбрать метод, допускающий минимальное число ложных отклонений гипотез и ложных принятий
Как и в одномерном случае, подход заключается в том, чтобы, ограничив меру ошибки первого рода малой величиной
выбрать процедуру, минимизирующую меру ошибки второго рода, т.е., максимизирующую мощность.
Типы семейств гипотез
Иерархические, неиерархические
Меры ошибки первого рода при множественной проверке
Существует большое количество величин, обобщающих определение ошибки первого рода на задачу множественной проверки гипотез. Наиболее популярны следующие:
- FWER — familywise error rate, групповая вероятность ошибки (первого рода):
- k-FWER, gFWER — generalized familywise error rate, обобщённая групповая вероятность ошибки (первого рода):
- FDP — false discovery proportion, доля ложных отклонений гипотез (среди всех отклонений):
- FDR — false discovery rate, средняя доля ложных отклонений гипотез (среди всех отклонений):
Связь между мерами ошибки первого рода
-
- При
(все рассматриваемые гипотезы верны)
Литература
- E. L. Lehmann, J. P. Romano: Testing statistical hypotheses. Springer, New York, 2005 (3rd edition), 786 pages. Chapter 9: Multiple testing and simultaneous inference.
Ссылки
- Multiple comparisons — статья из английской Википедии.