Коэффициент корреляции Пирсона

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м (→Статистическая проверка наличия корреляции)
м (→Слабые стороны)
Строка 34: Строка 34:
== Слабые стороны ==
== Слабые стороны ==
 +
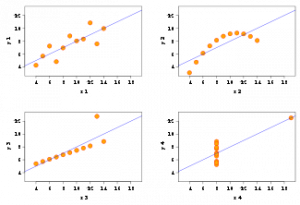
[[Image: Correlation.png|300px|thumb| Четыре различных набора данных, коэффициент корреляции на которых равен 0.81]]
 +
* Неустойчивость к выбросам.
-
* [[Image: Correlation.png|300px|thumb| Четыре различных набора данных, коэффициент корреляции на которых равен 0.81]] Неустойчивость к выбросам;
+
* С помощью коэффициента корреляции Пирсона можно определить силу линейной зависимости между величинами, другие виды взаимосвязей выявляются методами [[Регрессионный анализ|регрессионного анализа]].
-
 
+
-
* С помощью коэффициента корреляции можно определить линейную зависимость между величинами, другие взаимосвязи выявляются методами [[Регрессионный анализ|регрессионного анализа]];
+
* Необходимо понимать различие понятий "независимость" и "некоррелированность". Из первого следует второе, но не наоборот.
* Необходимо понимать различие понятий "независимость" и "некоррелированность". Из первого следует второе, но не наоборот.
Строка 43: Строка 43:
Для того, чтобы выяснить отношение между двумя переменными, часто необходимо избавиться от влияния третьей переменной. Рассмотрим пример 3-х переменных: x,y,z. Исключим влияние переменной z:
Для того, чтобы выяснить отношение между двумя переменными, часто необходимо избавиться от влияния третьей переменной. Рассмотрим пример 3-х переменных: x,y,z. Исключим влияние переменной z:
-
:: <tex>r_{xy \setminus z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{ \left(\ 1-r_{xz} \right)^2 \left(\ 1-r_{yz} \right)^2}} </tex> - [[Частная корреляция|частный коэффициент корреляции]].
+
:: <tex>r_{xy \setminus z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{ \left(\ 1-r_{xz} \right)^2 \left(\ 1-r_{yz} \right)^2}} </tex> – [[Частная корреляция|частный коэффициент корреляции]].
Для исключения влияния большего числа переменных:
Для исключения влияния большего числа переменных:
-
:: <tex>r_{ij \setminus vars}=\frac{-R_{ij}}{\sqrt{R_{ii}R_{jj}}} </tex>
+
:: <tex>r_{ij \setminus vars}=\frac{-R_{ij}}{\sqrt{R_{ii}R_{jj}}}</tex>
-
<tex> R_{ij} = (-1)^{i+j}M_{ij} </tex>, где <tex>M_{ij} </tex> - гл. минор матрицы коэффициентов корреляции переменных <tex> R =
+
<tex> R_{ij} = (-1)^{i+j}M_{ij} </tex>, где <tex>M_{ij} </tex> – главный минор матрицы коэффициентов корреляции переменных <tex> R =
\begin{pmatrix}
\begin{pmatrix}
1 & r_{12} & \dots & r_{1k} \\
1 & r_{12} & \dots & r_{1k} \\
Строка 56: Строка 56:
r_{k1} & \dots & \dots & 1
r_{k1} & \dots & \dots & 1
\end{pmatrix}
\end{pmatrix}
-
</tex>;
+
.</tex>
== Литература ==
== Литература ==

Версия 13:34, 11 января 2012

Содержание

Определение

Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя величинами.

Даны две выборки

x=\left( x_1, \cdots ,x_n \right), \; y=\left( y_1, \cdots ,y_n \right) ;

Коэффициент корреляции Пирсона рассчитывается по формуле:

r_{xy} = \frac {\sum_{i=1}^{n} \left( x_i-\bar{x} \right)\left( y_i-\bar{y} \right)}{\sqrt{\sum_{i=1}^{n} \left( x_i-\bar{x} \right)^2 \sum_{i=1}^{n} \left( y_i-\bar{y} \right)^2}} = \frac {cov(x,y)}{\sqrt{S_x^2S_y^2}}

где

\bar{x}, \; \bar{y} - средние значения выборок x и y;

S_x, \; S_y - среднеквадратичные отклонения;

r_{xy} \in \left[-1,1\right] − называют также теснотой линейной связи.

  • \left| r_{xy} \right| =1 , тогда x, y - линейно зависимы.
  • r_{xy}=0, тогда x, y - линейно независимы.

Статистическая проверка наличия корреляции

Гипотеза: H_0: отсутствует линейная связь между выборками x и y (r_{xy} = 0).

Статистика критерия:

T = \frac{r_{xy}\sqrt{n-2}}{sqrt{1-r^2_{xy}}} \sim t_{n-2} – распределение Стьюдента с n-2 степенями свободы.

Критерий:

T \in [t_\alpha,t_{1-\alpha}], где t_\alpha есть α-квантиль распределения Стьюдента.

Слабые стороны

Четыре различных набора данных, коэффициент корреляции на которых равен 0.81
Четыре различных набора данных, коэффициент корреляции на которых равен 0.81
  • Неустойчивость к выбросам.
  • С помощью коэффициента корреляции Пирсона можно определить силу линейной зависимости между величинами, другие виды взаимосвязей выявляются методами регрессионного анализа.
  • Необходимо понимать различие понятий "независимость" и "некоррелированность". Из первого следует второе, но не наоборот.

Для того, чтобы выяснить отношение между двумя переменными, часто необходимо избавиться от влияния третьей переменной. Рассмотрим пример 3-х переменных: x,y,z. Исключим влияние переменной z:

r_{xy \setminus z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{ \left(\ 1-r_{xz} \right)^2 \left(\ 1-r_{yz} \right)^2}} – частный коэффициент корреляции.

Для исключения влияния большего числа переменных:

r_{ij \setminus vars}=\frac{-R_{ij}}{\sqrt{R_{ii}R_{jj}}}

R_{ij} = (-1)^{i+j}M_{ij} , где M_{ij} – главный минор матрицы коэффициентов корреляции переменных R = \begin{pmatrix} 1 & r_{12} & \dots & r_{1k} \\ r_{21} & 1 & \dots & r_{2k}\\ \vdots & & & \vdots \\ r_{k1} & \dots & \dots & 1 \end{pmatrix} .

Литература

См. также

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB%D1%8F%D1%86%D0%B8%D0%B8_%D0%9F%D0%B8%D1%80%D1%81%D0%BE%D0%BD%D0%B0»
Личные инструменты