Биномиальное распределение

Материал из MachineLearning.

(Различия между версиями)

Версия 10:15, 20 декабря 2012

**Биномиальное распределение**
Функция вероятности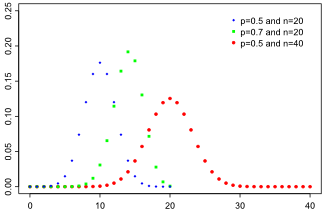
Функция распределения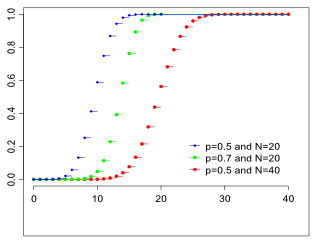
Параметры	$n \geq 0$ — число «испытаний» $0\leq p \leq 1$ — вероятность «успеха»
Носитель	$k \in \{0,\ldots,n\}\!$
Функция вероятности	${n \choose k}\,p^k q^{n-k} \!$
Функция распределения	$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
Математическое ожидание	$np\!$
Медиана	одно из $\{[np]-1, [np], [np]+1\}$
Мода	$\lfloor (n+1)\,p\rfloor\!$
Дисперсия	$npq\!$
Коэффициент асимметрии	$\frac{1-2p}{\sqrt{npq}}\!$
Коэффициент эксцесса	$\frac{1-6pq}{npq}\!$
Информационная энтропия	$\frac12 \log_2 \big( 2\pi e\, np(1-p) \big) + O \left( \frac{1}{n} \right)$
Производящая функция моментов	$(q + pe^t)^n \!$
Характеристическая функция	$(q + pe^{it})^n \!$

Содержание

1 Определение
2 Основные свойства
3 Асимптотические приближения при больших
4 Постулаты и их ложность
5 Литература
6 Ссылки

Определение

Биномиальное распределение — дискретное распределение вероятностей случайной величины $X,$ принимающей целочисленные значения $k=0,1,\ldots,n$ с вероятностями:

$P(X=k)={n \choose k}p^k(1-p)^{n-k}.$

Данное распределение характеризуется двумя параметрами: целым числом $n>0,$ называемым числом испытаний, и вещественным числом $p,$ $0\le p\le 1,$ называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из $n$ независимых испытаний, в каждом из которых может произойти "успех" с вероятностью $p,$ то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы $X=X_1+\cdots+X_n$ независимых слагаемых, имеющих распределение Бернулли.

Основные свойства

Характеристическая функция: $\phi(t)=(1+p(e^{it}-1))^n.$

Моменты:

Математическое ожидание: $MX=np.$
Дисперсия: $DX=np(1-p).$
Асимметрия: $\gamma_1=\frac{1-2p}{\sqrt{np(1-p)}};$ при $p=0.5$ распределение симметрично относительно центра $n/2.$

Асимптотические приближения при больших 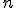$n$

Если значения $n$ велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).

Приближение Пуассона

Приближение распределением Пуассона применяется в ситуациях, когда значения $n$ большие, а значения $p$ близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром $\lambda=np.$

Строгая формулировка: если $n\to\infty$ и $p\to 0$ таким образом, что $np\to\lambda,$ то

$P(X=k)\to\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0, 1, 2, \ldots$

Более того, справедлива следующая оценка. Пусть $Y$ — случайная величина, имеющая распределение Пуассона с параметром $\lambda=np.$ Тогда для произвольного множества $B\subset\{0,1,2,\ldots\}$ справедливо неравенство:

$|P(X\in B) - P(Y\in B)|\le 2np^2.$

Доказательство и обзор более точных результатов, касающихся точности данного приближения, можно найти в [1, гл. III, §12].

Нормальное приближение

Приближение нормальным распределением используется в ситуациях, когда $n\to\infty,$ а $p$ фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применение которой основано на представлении $X$ в виде суммы $n$ слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной величины

$X'=\frac{X-MX}{\sqrt{DX}}=\frac{X-np}{\sqrt{npq},$ где $q=1-p,$

близко к стандартному нормальному.

Локальная теорема Муавра-Лапласа

Данная теорема используется для приближенного вычисления вероятностей отдельных значений биномиального распределения. Она утверждает [1, гл. I, §6], что равномерно по всем значениям $k,$ таким что $|k-np|=o(npq)^{2/3},$ имеет место

$P(X=k)\sim\frac{1}{\sqrt{2\pi npq}}e^{-\frac{(k-np)^2}{2npq}}=\frac{1}{\sqrt{npq}}\varphi\left(\frac{k-np}{\sqrt{npq}}\right),$

где $\varphi$ — плотность стандартного нормального распределения.

Интегральная теорема Муавра-Лапласа

На практике необходимость оценки вероятностей отдельных значений, которую дает локальная теорема Муавра-Лапласа, возникает нечасто. Гораздо более важно оценивать вероятности событий, включающих в себя множество значений. Для этого используется интегральная теорема, которую можно сформулировать в следующем виде [1, гл. I, §6]:

$\sup_{-\infty\le a<b\le\infty}\left|P\left(a<\frac{X-np}{\sqrt{npq}}\le b\right) - P(a<Z\le b)\right|\to 0$ при $n\to\infty,$

где случайная величина $Y$ имеет стандартное нормальное распределение $\mathcal{N}(0,1),$ и аппроксимирующая вероятность определяется по формуле

$P(a<Z\le b)=\Phi(b)-\Phi(a),$

где $\Phi(t)$ — функция распределения стандартного нормального закона: $\Phi(t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^t e^{-t^2/2}\,dt.$

Есть ряд результатов, позволяющих оценить скорость сходимости. В [1, гл. I, §6] приводится следующий результат, являющийся частным случаем теоремы Берри-Эссеена:

$\sup_{-\infty\le x\le\infty}|F_n(x)-\Phi(x)|\le\frac{p^2+q^2}{\sqrt{npq}},$

где $F_n(x)$ — функция распределения случайной величины $X'=\frac{X-np}{\sqrt{npq}}.$ На практике решение о том, насколько следует доверять нормальному приближению, принимают исходя из величины $npq.$ Чем она больше, тем меньше будет погрешность приближения.

Заметим, что асимптотический результат не изменится, если заменить строгие неравенства на нестрогие и наоборот. Предельная вероятность от такой замены также не поменяется, так как нормальное распределение абсолютно непрерывно и вероятность принять любое конкретное значение для него равна нулю. Однако исходная вероятность от такой замены может измениться, что вносит в формулу некоторую неоднозначность. Для больших значений $n$ изменение будет невелико, однако для небольших $n$ это может внести дополнительную погрешность.

Для устранения этой неоднозначности, а также повышения точности приближения рекомендуется задавать интересующие события в виде интервалов с полуцелыми границами. При этом приближение получается точнее. Это связано с тем интуитивно понятным соображением, что аппроксимация кусочно-постоянной функции (функции распределения биномиального закона) с помощью непрерывной функции дает более точные приближения между точками разрыва, чем в этих точках.

Пример

Пусть $n=20,$ $p=0.5.$ Оценим вероятность того, что число успехов будет отличаться от наиболее вероятного значения $10$ не более чем на $3$ . Заметим, что значение $npq=5$ очень мало, поэтому применение нормального приближения здесь довольно ненадежно.

Точная вероятность рассматриваемого события равна

$P(7\le X\le 13)\approx 0.8846.$

Применим нормальное приближение с той расстановкой неравенств, которая дана выше (снизу строгое, сверху нестрогое):

$P(7\le X\le 13)=P(6<X\le 13)=P\left(\frac{6-10}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{13-10}{\sqrt{5}}\right)=P\left(-\frac{4}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{3}{\sqrt{5}}\right)\approx P\left(-\frac{4}{\sqrt{5}}<Z\le\frac{3}{\sqrt{5}}\right)=\Phi\left(\frac{3}{\sqrt{5}}\right) - \Phi\left(-\frac{4}{\sqrt{5}}\right)\approx 0.8733.$

Ошибка приближения равна $0.0113$ .

Теперь построим приближение, используя интервал с концами в полуцелых точках:

$P(7\le X\le 13)=P(6.5<X< 13.5)=P\left(-\frac{3.5}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{3.5}{\sqrt{5}}\right)\approx P\left(-\frac{3.5}{\sqrt{5}}<Z\le\frac{3.5}{\sqrt{5}}\right)=\Phi\left(\frac{3.5}{\sqrt{5}}\right) - \Phi\left(-\frac{3.5}{\sqrt{5}}\right)\approx 0.8824.$

Ошибка приближения равна $0.0022$ — примерно в 5 раз меньше, чем в предыдущем подходе.

Постулаты и их ложность

Биномиальное распределение традиционной интерпретации основано на трёх постулатах [2]

Биномиальное распределение — распределение одной случайной величины;
Биномиальное распределение появляется в последовательности независимых испытаний (экспериментов);
Математическое ожидание биномиального распределения равно $np$ , где $n$ - конечное число независимых испытаний с двумя взаимно исключающими исходами каждое: положительный исход 1 c вероятностью $p$ и отрицательный исход 0 с вероятностью $q=1-p$ .

Ложность постулатов доказывается двумя теоремами[3,4].

Теорема 1. Биномиальное распределение не является распределением одной случайной величины.

Доказательство.

Если энциклопедически известно известно , что биномиальное распределение является частным случаем традиционной интерпретации полиномиального распределения как совместного распределения вероятностей независимых $X_1,\ldots, X _k$ случайных величин при сокращении в нём числа $k$ случайных величин до двух, то подставляя условие $k=2$ в формулу традиционной интерпретации полиномиального распределения

$P(X_1=n_1,\ldots,X_k=n_k)= \frac{n!}{n_1!\cdots n_k!}p_1^{n_1}\cdots p_k^{n_k},$

$2\le k \le n< \infty, \quad n_1+\ldots+n_k=n, \quad p_1+\ldots+p_k=1, \quad i=1,\ldots,k,$

получим формулу биномиального распределения не одной случайной величины, а двух случайных величин

$P(X_1=n_1, X_2=n_2)= \frac{n!}{n_1! n_2!} p_1^{n_1}p_2^{n_2},$

$2\le k \le n< \infty, \quad n_1+n_2=n, \quad p_1+p_2=1,$

что и требовалось доказать.

Примечание. Характер зависимости второй случайной величины от первой описан ниже.

Доказательство ложности второго и третьего постулатов.

Теорема 2. Биномиальное распределение не появляется в последовательности независимых испытаний (экспериментов) и его математическое ожидание не равно $np$ .

Доказательство.

Допустим, что

$np$

математическое ожидание биномиального распределения, появляющегося в последовательности независимых испытаний (экспериментов). Тогда при выполнении условия

$n>p^{-1}$

математическое ожидание этого распределения будет больше единицы, что противоречит аксиоматике Колмогорова, согласно которой сумма всех вероятностей распределения, включая и его математическое ожидание, должна быть равной единице.

Теорема 2 доказана.

Литература

1. Ширяев А.Н. Вероятность. — М.: МЦНМО, 2004.

Ссылки

Биномиальное распределение (Википедия)
Binomial distribution (Wikipedia)

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5»

Категория: Вероятностные распределения

@@ Строка 107: / Строка 107: @@
 Ошибка приближения равна <tex>0.0022</tex> &mdash; примерно в 5 раз меньше, чем в предыдущем подходе.
+== Постулаты и их ложность ==
+Биномиальное распределение традиционной интерпретации
+основано на трёх [[постулат  |постулатах]] [2]
+*Биномиальное распределение &mdash; распределение '''одной''' случайной величины;
+*Биномиальное распределение появляется в последовательности '''независимых''' испытаний (экспериментов);
+*Математическое ожидание биномиального распределения '''равно''' <tex>np</tex> , где <tex>n</tex> - конечное число независимых испытаний с двумя взаимно исключающими исходами каждое: положительный исход 1 c вероятностью <tex>p</tex> и отрицательный исход 0 с вероятностью <tex>q=1-p</tex>.
+Ложность постулатов доказывается двумя теоремами[3,4].
+'''Теорема 1. ''' Биномиальное распределение не является распределением одной случайной величины.
+'''Доказательство. '''
+Если энциклопедически известно известно , что биномиальное распределение является частным случаем традиционной интерпретации полиномиального распределения как совместного распределения вероятностей независимых <tex>X_1,\ldots, X _k</tex> случайных величин при сокращении в нём числа <tex>k</tex> случайных величин до двух, то подставляя условие <tex>k=2</tex> в формулу традиционной интерпретации полиномиального распределения
+::<tex>P(X_1=n_1,\ldots,X_k=n_k)= \frac{n!}{n_1!\cdots n_k!}p_1^{n_1}\cdots p_k^{n_k},</tex>
+::<tex>2\le k \le n< \infty, \quad n_1+\ldots+n_k=n, \quad p_1+\ldots+p_k=1, \quad i=1,\ldots,k, </tex>
+получим формулу биномиального распределения не одной случайной величины, а '''двух''' случайных величин
+::<tex> P(X_1=n_1, X_2=n_2)= \frac{n!}{n_1! n_2!} p_1^{n_1}p_2^{n_2}, </tex>
+::<tex>2\le k \le n< \infty, \quad n_1+n_2=n, \quad p_1+p_2=1,</tex>
+что и требовалось доказать.
+Примечание.
+Характер зависимости второй случайной величины от первой описан ниже.
+'''Доказательство ложности второго и третьего постулатов.'''
+'''Теорема 2.''' ''Биномиальное распределение не появляется в последовательности независимых испытаний (экспериментов) и его математическое ожидание'' '''не равно''' <tex>np</tex> .
+'''Доказательство.'''
+Допустим, что
+::<tex>np </tex>
+математическое ожидание биномиального распределения, появляющегося в последовательности независимых испытаний (экспериментов). Тогда при выполнении условия
+::<tex>n>p^{-1}</tex>
+математическое ожидание этого распределения будет больше единицы, что противоречит [[аксиоматика Колмогорова | аксиоматике Колмогорова]], согласно которой сумма всех вероятностей распределения, включая и его математическое ожидание, должна быть равной единице.
+Теорема 2 доказана.
 ==Литература==