Графические модели (курс лекций)/2013/Задание 3

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Модель авторегрессии)
(→Оформление задания)
Строка 108: Строка 108:
Присланный вариант задания должен содержать в себе:
Присланный вариант задания должен содержать в себе:
-
* Файл отчёта в формате PDF с указанием ФИО.
+
* Файл отчёта в формате PDF с указанием ФИО;
* Все исходные коды с необходимыми комментариями.
* Все исходные коды с необходимыми комментариями.
Строка 147: Строка 147:
!''Оценка параметров авторегрессии''
!''Оценка параметров авторегрессии''
|-
|-
-
|[w, A, Sigma, res, LH] = '''ar_fit'''(X, M)
+
|[w, A, Sigma, res, logLH] = '''ar_fit'''(X, M)
|-
|-
|ВХОД
|ВХОД
Строка 171: Строка 171:
|res — остатки авторегрессии (набор векторов <tex>\vec{x}_n-\vec{w}-\sum_{m=1}^MA_m\vec{x}_{n-m}</tex>), матрица размера (N-M) x d;
|res — остатки авторегрессии (набор векторов <tex>\vec{x}_n-\vec{w}-\sum_{m=1}^MA_m\vec{x}_{n-m}</tex>), матрица размера (N-M) x d;
|-
|-
-
|LH — логарифм правдоподобия настроенной модели авторегрессии, число.
+
|logLH — логарифм правдоподобия настроенной модели авторегрессии, число.
|}
|}
|}
|}
Строка 207: Строка 207:
|X — сгенерированная наблюдаемая последовательность, матрица размера N x d;
|X — сгенерированная наблюдаемая последовательность, матрица размера N x d;
|-
|-
-
|T — сгенерированная последовательность состояния, вектор длины N.
+
|T — сгенерированная последовательность состояний, вектор длины N.
|-
|-
|}
|}
Строка 217: Строка 217:
!''Оценка параметров авторегрессионной скрытой марковской модели с помощью ЕМ-алгоритма''
!''Оценка параметров авторегрессионной скрытой марковской модели с помощью ЕМ-алгоритма''
|-
|-
-
|[p, R, W, A, Sigmas] = '''arhmm_fit'''(X, K, M, param_name1, param_value1, ...)
+
|[p, R, W, A, Sigmas, logLH] = '''arhmm_fit'''(X, K, M, param_name1, param_value1, ...)
|-
|-
|ВХОД
|ВХОД
Строка 225: Строка 225:
|X — наблюдаемая последовательность, матрица размера N x d, первые M строк соответствуют начальной предыстории;
|X — наблюдаемая последовательность, матрица размера N x d, первые M строк соответствуют начальной предыстории;
|-
|-
-
|K — количество скрытых состояния, число;
+
|K — количество скрытых состояний, число;
|-
|-
|M — глубина авторегрессии, число;
|M — глубина авторегрессии, число;
Строка 262: Строка 262:
|A — авторегрессионные матрицы, массив размера d x Md x K;
|A — авторегрессионные матрицы, массив размера d x Md x K;
|-
|-
-
|Sigmas — матрицы ковариации шумов, массив размера d x d x K.
+
|Sigmas — матрицы ковариации шумов, массив размера d x d x K;
|-
|-
 +
|logLH — логарифм правдоподобия, число.
|}
|}
|}
|}

Версия 01:05, 31 марта 2013

Основная статья: Графические модели (курс лекций)


Формулировка задания находится в стадии подготовки. Убедительная просьба не приступать к выполнению задания до тех пор, пока это предупреждение не будет удалено.


Начало выполнения задания: 18 марта 2013 г.;
Срок сдачи: 7 апреля 2013 г. (воскресенье), 23:59.

Среда для выполнения задания — MATLAB. Неэффективная реализация кода может негативно отразиться на оценке.

Содержание

Модель авторегрессии

Графическая модель авторегрессии 1-го порядка
Графическая модель авторегрессии 1-го порядка

Случайный процесс с дискретным временем \{\vec{x}_n\}_{n=1}^N, \vec{x}_n\in\mathbb{R}^d называется авторегрессией первого порядка, если

\vec{x}_n = \vec{w} + A\vec{x}_{n-1} + \vec{\varepsilon}_n,\quad \vec{\varepsilon}_n\sim\mathcal{N}(\vec{0},\Sigma).

Здесь \vec{w}\in\mathbb{R}^d — параметр сдвига, A\in\mathbb{R}^{d\times d} — авторегрессионная матрица, \Sigma\in\mathbb{R}^{d\times d} — матрица ковариации шума, шумовые компоненты \vec{\varepsilon}_n предполагаются независимыми. Процесс авторегрессии является стационарным, если все собственные значения матрицы A (включая комплексные) по модулю меньше единицы. Мат.ожидание \vec{\mu} стационарного процесса авторегрессии определяется как

\vec{\mu} = (I-A)^{-1}\vec{w},

где I — единичная матрица размера d\times d.

В терминах графических моделей авторегрессия первого порядка представляет собой байесовскую сеть с графом вида цепочка (см. рис.), где совместное распределение задается как

p(X|\vec{w},A,\Sigma,\vec{x}_0)=\prod_{n=1}^N\mathcal{N}(\vec{x}_n|\vec{w}+A\vec{x}_{n-1},\Sigma),

а \vec{x}_0 — начальная предыстория.

Авторегрессия M-го порядка задается как

\vec{x}_n = \vec{w}+\sum_{m=1}^MA_m\vec{x}_{n-m}+ \vec{\varepsilon}_n,\quad \vec{\varepsilon}_n\sim\mathcal{N}(\vec{0},\Sigma).

Здесь шумовые компоненты \vec{\varepsilon}_n по-прежнему предполагаются независимыми. Очевидно, что авторегрессия M-го порядка может быть сведена к авторегрессии первого порядка как

\tilde{\vec{x}}_n = \tilde{\vec{w}} + \tilde{A}\tilde{\vec{x}}_{n-1} + \tilde{\vec{\varepsilon}}_n,\quad \tilde{\vec{w}} = \begin{bmatrix}\vec{w}\\ 0\\ \vdots \\ 0\end{bmatrix},\quad \tilde{\vec{x}}_n = \begin{bmatrix}\vec{x}_n\\ \vec{x}_{n-1}\\ \vdots \\ \vec{x}_{n-M}\end{bmatrix},\quad \tilde{A} = \begin{bmatrix}A_1 & A_2 & A_3 & \dots & A_{M-1} & A_M\\ I & 0 & 0 & \dots & 0 & 0\\ 0 & I & 0 & \dots & 0 & 0\\ \dots \\ 0 & 0 & 0 & \dots & I & 0 \end{bmatrix},\quad \tilde{\vec{\varepsilon}}_n = \begin{bmatrix}\vec{\varepsilon}_n \\ 0 \\ \vdots \\ 0\end{bmatrix}.

Поэтому авторегрессия M-го порядка является стационарной, если все собственные значения матрицы \tilde{A} по модулю меньше единицы. Мат.ожидание стационарной регрессии M-го порядка определяется как

\vec{\mu} = (I-A_1-\dots-A_M)^{-1}\vec{w}.

В дальнейшем для удобства набор матриц A_1,\dots,A_M будем обозначать через \mathcal{A}.

Графическая модель авторегрессии 2-го порядка
Графическая модель авторегрессии 2-го порядка

В терминах графических моделей авторегрессия M-го порядка представляет собой байесовскую сеть с графом, показанном на рис. справа, где совместное распределение задается как

p(X|\vec{w},\mathcal{A},\Sigma,X_0)=\prod_{n=1}^N\mathcal{N}(\vec{x}_n|\vec{w}+\sum_{m=1}^MA_m\vec{x}_{n-m},\Sigma),

а X_0=\{\vec{x}_0,\vec{x}_{-1},\dots,\vec{x}_{1-M}\} — начальная предыстория.

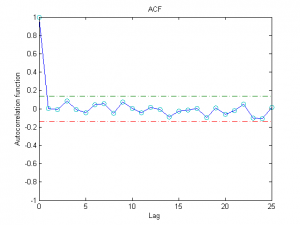
Пример выборочной автокорреляционной функции с отсутствием значимых автокорреляций
Пример выборочной автокорреляционной функции с отсутствием значимых автокорреляций

Одним из способов определения адекватности моделирования данных с помощью модели авторегрессии является исследование остатков

\hat{\varepsilon}_n = \vec{x}_n - \hat{\vec{w}} - \sum_{m=1}^M\hat{A}_m\vec{x}_{n-m},

где \hat{\vec{w}},\hat{A} — оценки параметров авторегрессии (например, оценки максимального правдоподобия). Для успешного объяснения данных с помощью авторегрессии необходимо, чтобы остатки не были коррелированы по времени. Другими словами, выборочная автокорреляционная функция

ACF(\tau) = c_{\tau}/c_0,\quad c_{\tau} = \frac{1}{N-\tau}\sum_{n = \tau+1}^N(\varepsilon_n - \bar{\varepsilon})(\varepsilon_{n-\tau} - \bar{\varepsilon}),\quad \bar{\varepsilon} = \frac{1}{N}\sum_n\varepsilon_n

должна лежать в интервале \pm \frac{z_{1-\alpha/2}}{\sqrt{N}} для всех \tau. Здесь через z_{\beta} обозначена \beta-квантиль одномерного нормального распределения. Для уровня значимости \alpha=0.05 соответствующая квантиль равна 1.96.

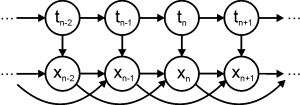
Авторегрессионная скрытая марковская модель

Графическая модель авторегрессионной скрытой марковской модели 2-го порядка
Графическая модель авторегрессионной скрытой марковской модели 2-го порядка

Авторегрессионная скрытая марковская модель M-го порядка — это байесовская сеть, граф которой показан на рис. справа, а совместное распределение задается как

p(X,T|\theta,X_0)=p(t_1)\prod_{n=2}^Np(t_n |t_{n-1})\prod_{n=1}^Np(\vec{x}_n |t_n,\vec{x}_{n-1},\dots,\vec{x}_{n-M}).

Здесь t_n\in\{1,\dots,K\} — скрытые дискретные состояния, \vec{x}_n\in\mathbb{R}^d — непрерывные наблюдаемые переменные. Априорное распределение p(t_1) задается вектором [\pi_1,\ldots,\pi_K], причем все \pi_k\ge 0 и \sum_k\pi_k=1. Распределение p(t_n |t_{n-1}) задается матрицей перехода R размера K\times K, где в ij-ой позиции стоит вероятность перехода из состояния i в состояние j. Все элементы этой матрицы неотрицательны, а сумма элементов по каждой строке равна единице. Модель генерации данных соответствует модели авторегрессии, в которой параметры \vec{w},\mathcal{A},\Sigma зависят от текущего состояния t_n. Таким образом,

p(\vec{x}_n|t_n,\vec{x}_{n-1},\dots,\vec{x}_{n-M})=\mathcal{N}(\vec{x}_n|\vec{w}_{t_n}+\sum_{m=1}^MA_{m,t_n}\vec{x}_{n-m},\Sigma_{t_n}).

В результате полный набор параметров модели состоит из \vec{\pi},R,\{\vec{w}_k,\mathcal{A}_k,\Sigma_k\}_{k=1}^K. Глубина авторегрессии M, количество скрытых состояний K, а также начальная предыстория X_0=\{\vec{x}_0,\vec{x}_{-1},\dots,\vec{x}_{1-M}\} задаются пользователем.

Формулировка задания

  1. Для модели авторегрессии M-го порядка:
    • Вывести формулы для оценки параметров модели \vec{w},\mathcal{A},\Sigma по наблюдениям \{\vec{x}_n\}_{n=1}^N с помощью метода максимального правдоподобия;
    • Реализовать процедуру генерации сигнала из модели авторегрессии;
    • Реализовать процедуру оценки параметров \vec{w},\mathcal{A},\Sigma по методу максимального правдоподобия;
  2. Провести следующие эксперименты с авторегрессией M-го порядка:
    • Сгенерировать данные из модели авторегрессии, а затем восстановить параметры по методу максимального правдоподобия. Как ведут себя значение правдоподобия, авторегрессионные остатки и восстановленные параметры при глубине авторегрессии меньше истинного значения, равного истинному значению и больше истинного значения? Какой объем данных необходим для адекватного восстановления параметров модели?
    • Сгенерировать данные из модели случайного процесса, отличного от авторегрессии. К чему приводит попытка объяснения таких данных с помощью авторегрессии?
  3. Для авторегрессионной скрытой марковской модели:
    • Вывести формулы ЕМ-алгоритма для оценки параметров модели \vec{\pi},R,\{\vec{w}_k,\mathcal{A}_k,\Sigma_k}_{k=1}^K, при этом предусмотреть ситуации, когда часть параметров задается пользователем;
    • Реализовать процедуру генерации сигнала из модели;
    • Реализовать процедуру оценки параметров модели с помощью EM-алгоритма;
    • Реализовать процедуру оценки скрытых состояний по наблюдаемым данным и параметрам модели с помощью алгоритма Витерби;
  4. Провести следующие эксперименты с авторегрессионной скрытой марковской моделью:
  5. Применить авторегрессионную скрытую марковскую модель для моделирования и сегментации движений в базе данных mocap.

Рекомендации по выполнению задания

1. Вывод формул для авторегрессии и авторегрессионной скрытой марковской модели удобно осуществлять путем введения обозначений

\vec{y}_n = [\vec{x}_{n-1}^T\ \vec{x}_{n-2}^T\ \dots \vec{x}_{n-M}^T\ 1]^T,\quad B = [A_1\ A_2\ \dots A_M\ \vec{w}].

Тогда выражение \vec{x}_n - \vec{w} - \sum_{m=1}^MA_m\vec{x}_{n-m} можно лаконично записать как \vec{x}_n-B\vec{y}_n.

После вывода необходимых формул рекомендуется убедиться в том, что эти формулы переходят в стандартные формулы для оценки параметров многомерного нормального распределения (в том числе в рамках скрытой марковской модели) при обнулении всех A.

2. При тестировании ЕМ-алгоритма рекомендуется отслеживать монотонное возрастание логарифма неполного правдоподобия в итерациях.

Оформление задания

Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «[ГМ13] Задание 3 <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций.

Присланный вариант задания должен содержать в себе:

  • Файл отчёта в формате PDF с указанием ФИО;
  • Все исходные коды с необходимыми комментариями.

 

Генерация выборки из модели авторегрессии
X = ar_generate(N, w, A, Sigma, X0)
ВХОД
N — количество точек в генерируемой последовательности, число;
w — параметр сдвига, вектор длины d;
A — набор матриц в форме [A_1\ A_2\ \dots\ A_M], матрица размера d x Md;
Sigma — матрица ковариации для нормального шума, матрица размера d x d;
X0 — (необязательный параметр) начальная предыстория, матрица размера M x d;
ВЫХОД
X — сгенерированная последовательность, матрица размера N x d.

Если начальная предыстория X_0 не задана, то X_0 выбирается равной мат.ожиданию процесса авторегрессии.

Оценка параметров авторегрессии
[w, A, Sigma, res, logLH] = ar_fit(X, M)
ВХОД
X — наблюдаемая последовательность, матрица размера N x d, первые M строк соответствуют начальной предыстории;
M — глубина авторегрессии, число;
ВЫХОД
w — параметр сдвига авторегрессии, вектор длины d;
A — набор матриц в форме [A_1\ A_2\ \dots\ A_M], матрица размера d x Md;
Sigma — матрица ковариации нормального шума, матрица размера d x d;
res — остатки авторегрессии (набор векторов \vec{x}_n-\vec{w}-\sum_{m=1}^MA_m\vec{x}_{n-m}), матрица размера (N-M) x d;
logLH — логарифм правдоподобия настроенной модели авторегрессии, число.

 

Генерация выборки из авторегрессионной скрытой марковской модели
[X, T] = arhmm_generate(N, p, R, W, A, Sigmas, X0)
ВХОД
N — количество точек в генерируемой последовательности, число;
p — априорное распределение на t_1, вектор длины K;
R — матрица перехода размера K x K;
W — параметры сдвига авторегрессии для каждого состояния, матрица размера d x K;
A — авторегрессионные матрицы A для каждого состояния, массив размера d x Md x K;
Sigmas — матрицы ковариации шума для каждого состояния, массив размера d x d x K;
X0 — начальная предыстория, матрица размера M x d;
ВЫХОД
X — сгенерированная наблюдаемая последовательность, матрица размера N x d;
T — сгенерированная последовательность состояний, вектор длины N.

Если начальная предыстория X_0 не задана, то X_0 выбирается равной мат.ожиданию процесса авторегрессии, соответствующего сгенерированному состоянию t_1.

Оценка параметров авторегрессионной скрытой марковской модели с помощью ЕМ-алгоритма
[p, R, W, A, Sigmas, logLH] = arhmm_fit(X, K, M, param_name1, param_value1, ...)
ВХОД
X — наблюдаемая последовательность, матрица размера N x d, первые M строк соответствуют начальной предыстории;
K — количество скрытых состояний, число;
M — глубина авторегрессии, число;
(param_name, param_value) — набор необязательных параметров, следующие имена и значения возможны:
'max_iter' — максимальное число итераций ЕМ-алгоритма, по умолчанию = 100;
'num_start' — количество запусков из случайных начальных приближений, по умолчанию = 1;
'p' — известное априорное распределение на состояния, в случае задания не оптимизируется ЕМ-алгоритмом, по умолчанию = [];
'R' — известная матрица перехода между состояниями, в случае задания не оптимизируется ЕМ-алгоритмом, по умолчанию = [];
'W' — известный набор параметров сдвига, в случае задания не оптимизируется ЕМ-алгоритмом, по умолчанию = [];
'A' — известный набор авторегрессионных матриц, в случае задания не оптимизируется ЕМ-алгоритмом, по умолчанию = [];
'Sigmas' — известный набор матриц ковариации шума, в случае задания не оптимизируется ЕМ-алгоритмом, по умолчанию = [];
'display' — режим отображения, true или false, если true, то отображается текущая информация, например, номер запуска, номер итерации, текущее значение правдоподобия и т.д.
ВЫХОД
p — априорное распределение на состояние, вектор длины K;
R — матрица перехода между состояниями, матрица размера K x K;
W — параметр сдвига авторегрессий, матрица размера d x K;
A — авторегрессионные матрицы, массив размера d x Md x K;
Sigmas — матрицы ковариации шумов, массив размера d x d x K;
logLH — логарифм правдоподобия, число.

 

Сегментация выборки с помощью алгоритма Витерби
T = arhmm_segment(X, p, R, W, A, Sigmas)
ВХОД
X — наблюдаемая последовательность, матрица размера N x d, первые M строк соответствуют начальной предыстории;
p — априорное распределение на t_1, вектор длины K;
R — матрица перехода размера K x K;
W — параметры сдвига авторегрессии для каждого состояния, матрица размера d x K;
A — авторегрессионные матрицы A для каждого состояния, массив размера d x Md x K;
Sigmas — матрицы ковариации шума для каждого состояния, массив размера d x d x K;
ВЫХОД
T — номера состояний в каждый момент времени, вектор длины N.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%93%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2013/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_3»
Личные инструменты