Метод главных компонент

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Литература)
(→Внешние ссылки)
Строка 59: Строка 59:
== Внешние ссылки ==
== Внешние ссылки ==
* [http://pca.narod.ru/ Нелинейный метод главных компонент]
* [http://pca.narod.ru/ Нелинейный метод главных компонент]
 +
* [http://en.wikipedia.org/wiki/Principal_components_analysis Principal components analysis at wikipedia.org]
 +
* [http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82 Метод главных компонент на wikipedia.org]
{{Заготовка}}
{{Заготовка}}

Версия 08:01, 30 июня 2008

Метод главных компонент — способ снижения размерности пространства данных. Он заключается в нахождении линейного ортогонального преобразования исходной матрицы данных в пространство меньшей размерности. При этом выбираются такая ортогональная система координат, которая обеспечивает наименьшую потерю информации в исходных данных. Последнее подразуменает минимальную среднеквадратичную ошибку при проекции данных в пространство заданной размерности.

Содержание

Определение метода главных компонент

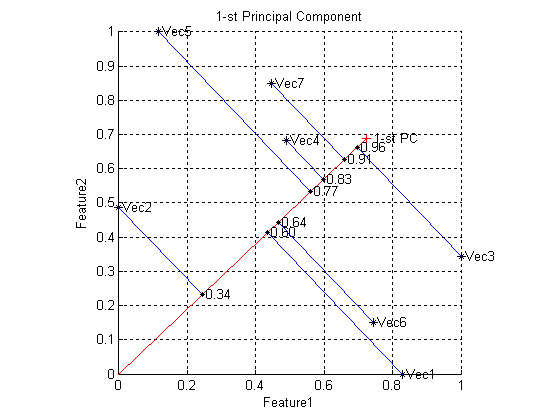
Векторы-строки матрицы исходных данных  показаны звездочками. Красным крестом отмечен первый вектор-столбец матрицы вращения . Точками отмечены проекции векторов на новую систему координат. Сумма квадратов длин синих линий есть ошибка — количество информации, утраченной при снижении размерности пространства.
Векторы-строки матрицы исходных данных A показаны звездочками. Красным крестом отмечен первый вектор-столбец матрицы вращения V. Точками отмечены проекции векторов на новую систему координат. Сумма квадратов длин синих линий есть ошибка — количество информации, утраченной при снижении размерности пространства.

Одной из задач аппроксимации является задача приближения множества векторов-строк \mathbf{a}_i матрицы A их проекциями на некоторую новую ортогональную систему координат. Эта система отыскивается на множестве преобразований вращений V начальной системы координат. При этом множество аппроксимируемых векторов \mathbf{a}_i, i=1,...,m, отображается в новое множество векторов \mathbf{z}_i, где \mathbf{a}_i,\mathbf{z}_i\in\mathbb{R}^n. Оператором отображения

Z=A^TV

является ортонормальная матрица V, то есть VV^T=I — единичная матрица. Столбцы Z называются главными компонентами матрицы A. Матрица V строится таким образом, что среднеквадратическая разность между векторами \mathbf{a}_i и проекцией этих векторов на ортогональную систему координат, заданных \mathbf{z}_i минимальна. Наиболее удобным способом получения матрицы V является сингулярное разложение матрицы A:

A=U\Lambda V^T.

Метод главных компонент позволяет с помощью k первых главных компонент можно восстановить исходную матрицу с минимальной ошибкой. Критерий минимального значения суммы квадратов расстояния от векторов-столбцов матрицы данных до их проекций на первую главную компоненту называется критерием наибольшей информативности C.Р. Рао. Кроме того, матрица V выполняет декоррелирующее преобразование, называемое также преобразованием Карунена-Лоэва. В результате этого преобразования исчезает возможная корреляция между векторами-столбцами исходной матрицы A.

Рао было показано, что строки матрицы V есть собственные векторы ковариационной матрицы
\Sigma=A^TA,

где матрица A центрирована — из каждого ее столбца вычтено среднее значение по этому столбцу.

Понятие наибольшей информативности

Рассмотрим n-мерную случайную величину A с ковариационной матрицей \Sigma=A^TA. Обозначим \mu_1,\dots,\mu_n — соответствующие собственные числа и \mathbf{v}_1,\dots,\mathbf{v}_n — собственные векторы матрицы \Sigma. Заметим, что собственные числа и элементы собственных векторов матрицы \Sigma всегда действительны. Тогда по теореме о собственных числах

\Sigma=\sum_{i=1}^n\mu_i\mathbf{v}_i\mathbf{v}_i^T,  I=\sum_{i=1}^n\mathbf{v}_i\mathbf{v}_i^T,
\mathbf{v}_i^T{\Sigma}\mathbf{v}_i=\mu_i,  \mathbf{v}_i^T{\Sigma}\mathbf{v}_j=0,   i\neq{j}. (*)

Случайная величина \mathbf{z}_i=\mathbf{v}_i^TA называется i-й главной компонентой случайной величины A. Матрица вращения V составлена из векторов-столбцов \mathbf{v}_1,\ldots,\mathbf{v}_n. Матрица главных компонент Z=A^TV имеет следующие свойства.

Смотри также

Литература

  • Рао С.Р. Линейные статистические методы и их применения. М.: Наука. 1968. — С. 530-533.
  • Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности. М.: Финансы и статистика. 1989.
  • Jolliffe I.T. Principal Component Analysis, Springer Series in Statistics. Springer. 2002.
  • Pearson, K. (1901). "On Lines and Planes of Closest Fit to Systems of Points in Space". Philosophical Magazine 2 (6): 559–572. [1]

Внешние ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82»
Личные инструменты