Графические модели (курс лекций)/2013/Задание 4

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(задание)
м
 
(4 промежуточные версии не показаны)
Строка 1: Строка 1:
-
{{stop|
 
-
'''Задание находится на стадии разработки.'''<br/>
 
-
Не приступайте к выполнению задания, пока данное объявление не убрано.
 
-
}}
 
-
 
{{main|Графические модели (курс лекций)}}
{{main|Графические модели (курс лекций)}}
-
 
+
__NOTOC__
-
{{TOCright|300px}}
+
{|
{|
Строка 43: Строка 37:
|}
|}
-
== Марковское случайное поле ==
+
=== Марковское случайное поле ===
[[Изображение:SMAIS11_grid.jpg‎|100px|thumb|Система соседства — прямоугольная решетка]]
[[Изображение:SMAIS11_grid.jpg‎|100px|thumb|Система соседства — прямоугольная решетка]]
Марковское случайное поле (MRF) — графическая модель, энергия которой записывается в виде:<br>
Марковское случайное поле (MRF) — графическая модель, энергия которой записывается в виде:<br>
<tex>
<tex>
-
E(X) = \sum_{p \in P} D_p(x_p) + \sum_{(p, q) \in E} V_{pq}(x_p, x_q),
+
E(X) = \sum_{p \in P} D_p(x_p) + \sum_{(p, q) \in \mathcal{E}} V_{pq}(x_p, x_q),
</tex><br>
</tex><br>
-
где P — множество индексов переменных, E — система соседства, D — унарные потенциалы, V — бинарные потенциалы.
+
где P — множество индексов переменных, <tex>\mathcal{E} </tex> — система соседства, D — унарные потенциалы, V — парные потенциалы.
Рассмотрим модель со следующими ограничениями:
Рассмотрим модель со следующими ограничениями:
*переменные <tex> x_p </tex> дискретны и принимают значения из множества {1,…,K}, K ≥ 2,
*переменные <tex> x_p </tex> дискретны и принимают значения из множества {1,…,K}, K ≥ 2,
-
*система соседства E — прямоугольная решетка,
+
*система соседства <tex>\mathcal{E} </tex> — прямоугольная решетка,
-
*бинарные потенциалы V представимы в виде произведения множителя, не зависящего от значений соседних переменных, и множителя, зависящего только от них: <tex>V_{pq} = c_{pq} d(x_p, x_q) </tex>.
+
*парные потенциалы V представимы в виде произведения множителя, не зависящего от значений соседних переменных, и множителя, зависящего только от них: <tex>V_{pq} = c_{pq} d(x_p, x_q) </tex>.
-
 
+
-
В рамках этого задания требуется:
+
-
#реализовать алгоритм поиска конфигурации <tex>X</tex>, обладающей минимальной энергией (α-расширение или αβ-замена),
+
-
#протестировать реализованный алгоритм на модельных задачах,
+
-
#применить реализованный алгоритм для задачи стерео,
+
-
#сравнить алгоритмы α-расширение и αβ-замена на задаче стерео.
+
=== MRF для стерео ===
=== MRF для стерео ===
Строка 70: Строка 58:
*Унарные потенциалы должны показывать, насколько хорошо выбранные пиксели двух изображений соответствуют друг другу. В простейшем случае можно взять евклидово расстояние между цветами пикселей в формате [http://en.wikipedia.org/wiki/YUV YUV]. Более совершенные унарные потенциалы описаны в статье: S. Birchfield, C. Tomasi, A pixel dissimilarity measure that is insensitive to image sampling, IEEE TPAMI, 20(4):401–409, 1998, http://ce.sharif.edu/~elno/disparitymap/Papers/dissimilarity_pami1998.pdf.
*Унарные потенциалы должны показывать, насколько хорошо выбранные пиксели двух изображений соответствуют друг другу. В простейшем случае можно взять евклидово расстояние между цветами пикселей в формате [http://en.wikipedia.org/wiki/YUV YUV]. Более совершенные унарные потенциалы описаны в статье: S. Birchfield, C. Tomasi, A pixel dissimilarity measure that is insensitive to image sampling, IEEE TPAMI, 20(4):401–409, 1998, http://ce.sharif.edu/~elno/disparitymap/Papers/dissimilarity_pami1998.pdf.
*В качестве расстояния d между метками соседних переменных можно взять усеченный модуль разности: <tex>d(x_p, x_q) = |x_p - x_q| [x_p-x_q < L] + L [x_p-x_q \geq L]</tex>, L ≥ 0 — параметр.
*В качестве расстояния d между метками соседних переменных можно взять усеченный модуль разности: <tex>d(x_p, x_q) = |x_p - x_q| [x_p-x_q < L] + L [x_p-x_q \geq L]</tex>, L ≥ 0 — параметр.
-
*Веса ребер c могут иметь большие значения там, где градиент на изображении мал, и маленькие значения там, где градиент большой. Например: <tex>c_{pq} = a \exp(-\|I_p - I_q\| / s)</tex>, где a ≥ 0, s ≥ 0 — параметры.
+
*Веса ребер c могут иметь большие значения там, где градиент на изображении мал, и маленькие значения там, где градиент большой.
-
В рамках данного задания вариант 1 работает с алгоритмом α-расширение, вариант 2 — αβ-замена. Далее в задании алгоритм соответствующего варианта обозначается ''алгоритм''.
+
В рамках данного задания рассматривается задача поиска конфигурации, обладающей минимальной энергией. Вариант 1 работает с алгоритмом α-расширение, вариант 2 — αβ-замена. Далее в задании алгоритм соответствующего варианта обозначается ''алгоритм''.
=== Задание ===
=== Задание ===
* Вывести все формулы, использующиеся в вашей реализации ''алгоритма'' (сведение шага алгоритма к разрезу графа).
* Вывести все формулы, использующиеся в вашей реализации ''алгоритма'' (сведение шага алгоритма к разрезу графа).
-
* Реализовать алгоритм ''алгоритм'', используя выданный код разрезов графов.
+
* Реализовать ''алгоритм'', используя выданный код разрезов графов.
-
* Протестировать алгоритм ''алгоритм'' на модельных данных.
+
* Протестировать ''алгоритм'' на модельных данных.
* Реализовать процедуру решения задачи стерео.
* Реализовать процедуру решения задачи стерео.
-
* Подобрать параметры так, чтобы на выданных стереопарах достигался хороший результат. Набор параметров может быть своим для каждой стереопары.
+
* Подобрать унарные и парные потенциалы так, чтобы на выданных стереопарах достигался хороший (относительно истинных смещений) результат. Набор унарных и парных потенциалов, а также их параметров может быть своим для каждой стереопары.
* На нескольких стереопарах из предыдущего пункта сравнить работу алгоритмов α-расширение и αβ-замена. Реализацию недостающего алгоритма можно взять у товарища, выполняющего другой вариант (в отчете обязательно указывать, чей код вы используете). Требуется провести сравнение по энергии получаемого решения, по времени работы, по визуальному качеству решения. Все выводы должны быть подтверждены числами, графиками, картинками.
* На нескольких стереопарах из предыдущего пункта сравнить работу алгоритмов α-расширение и αβ-замена. Реализацию недостающего алгоритма можно взять у товарища, выполняющего другой вариант (в отчете обязательно указывать, чей код вы используете). Требуется провести сравнение по энергии получаемого решения, по времени работы, по визуальному качеству решения. Все выводы должны быть подтверждены числами, графиками, картинками.
* Написать отчет в формате PDF с описанием всех проведенных исследований.
* Написать отчет в формате PDF с описанием всех проведенных исследований.
Строка 113: Строка 101:
|&nbsp;&nbsp;'maxIter' — максимально допустимое число итераций алгоритма (по умолчанию = 500);
|&nbsp;&nbsp;'maxIter' — максимально допустимое число итераций алгоритма (по умолчанию = 500);
|-
|-
-
|&nbsp;&nbsp;'display' — параметр типа logical: если true, то при каждом запуске алгоритма разреза графа нужно выводить на экран номер итерации, номер расширяемой метки, текущее значение энергии;
+
|&nbsp;&nbsp;'display' — параметр типа logical: если true, то при каждом запуске алгоритма разреза графа нужно выводить на экран номер итерации, номера обрабатываемых меток, текущее значение энергии;
 +
|-
 +
|&nbsp;&nbsp;'numStart' — количество запусков из разных начальных приближений;
 +
|-
 +
|&nbsp;&nbsp;'randOrder' — параметр типа logical: если true, то при каждом запуске использовать случайный порядок меток α и β;
|}
|}
|-
|-
Строка 165: Строка 157:
=== Оформление задания ===
=== Оформление задания ===
-
Выполненный вариант задания необходимо прислать письмом по адресу ''bayesml@gmail.com'' с темой «Задание 4. ФИО, вариант X». Убедительная просьба присылать выполненное задание '''только один раз''' с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.
+
Выполненный вариант задания необходимо прислать письмом по адресу ''bayesml@gmail.com'' с темой «[ГМ13] задание 4, вариант X, фамилия». Убедительная просьба присылать выполненное задание '''только один раз''' с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.
Письмо должно содержать:
Письмо должно содержать:

Текущая версия

Основная статья: Графические модели (курс лекций)


Задача стерео: восстановление карты смещений по стереопарам.
Задача стерео: восстановление карты смещений по стереопарам.

Начало выполнения задания: 9 апреля 2013 г.;
Срок сдачи: 21 апреля 2013 г. (воскресенье), 23:59.

Среда для выполнения задания — MATLAB. Неэффективная реализация кода может негативно отразиться на оценке.

Задание состоит из двух вариантов. Распределение вариантов задания по студентам:

Вариант 1: α-расширение Вариант 2: αβ-замена
Кондрашкин Д. Нижибицкий Е.
Остапец А. Фонарев А.
Ромов П. Лобачева Е.
Куракин А. Новиков М.
Березин А. Любимцева М.
Исмагилов Т. Потапенко А.
Шаймарданов И. Зак Е.
Малышева Е. Огнева Д.
Морозова Д. Борисов М.
Гавриков М.

Марковское случайное поле

Система соседства — прямоугольная решетка
Система соседства — прямоугольная решетка

Марковское случайное поле (MRF) — графическая модель, энергия которой записывается в виде:
E(X) = \sum_{p \in P} D_p(x_p) + \sum_{(p, q) \in \mathcal{E}} V_{pq}(x_p, x_q),
где P — множество индексов переменных, \mathcal{E} — система соседства, D — унарные потенциалы, V — парные потенциалы.

Рассмотрим модель со следующими ограничениями:

  • переменные x_p дискретны и принимают значения из множества {1,…,K}, K ≥ 2,
  • система соседства \mathcal{E} — прямоугольная решетка,
  • парные потенциалы V представимы в виде произведения множителя, не зависящего от значений соседних переменных, и множителя, зависящего только от них: V_{pq} = c_{pq} d(x_p, x_q) .

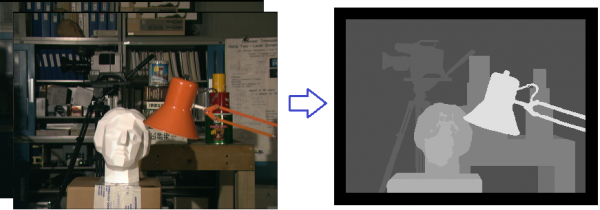
MRF для стерео

Задача стерео состоит в сопоставлении каждому пикселю одного изображения пикселя другого изображений. В рамках данного задания рассматривается выровненное стерео, что означает, что соответствующие пиксели лежат на одной горизонтальной линии. В этих условиях переменные имеют смысл смещений по горизонтали (диспаритетов).

Для задачи стерео марковское случайное поле строится следующим образом:

  • Переменная x_p соответствуют пикселям одного из изображений.
  • Используется стандартная 4-х связная система соседства.
  • Унарные потенциалы должны показывать, насколько хорошо выбранные пиксели двух изображений соответствуют друг другу. В простейшем случае можно взять евклидово расстояние между цветами пикселей в формате YUV. Более совершенные унарные потенциалы описаны в статье: S. Birchfield, C. Tomasi, A pixel dissimilarity measure that is insensitive to image sampling, IEEE TPAMI, 20(4):401–409, 1998, http://ce.sharif.edu/~elno/disparitymap/Papers/dissimilarity_pami1998.pdf.
  • В качестве расстояния d между метками соседних переменных можно взять усеченный модуль разности: d(x_p, x_q) = |x_p - x_q| [x_p-x_q < L] + L [x_p-x_q \geq L], L ≥ 0 — параметр.
  • Веса ребер c могут иметь большие значения там, где градиент на изображении мал, и маленькие значения там, где градиент большой.

В рамках данного задания рассматривается задача поиска конфигурации, обладающей минимальной энергией. Вариант 1 работает с алгоритмом α-расширение, вариант 2 — αβ-замена. Далее в задании алгоритм соответствующего варианта обозначается алгоритм.

Задание

  • Вывести все формулы, использующиеся в вашей реализации алгоритма (сведение шага алгоритма к разрезу графа).
  • Реализовать алгоритм, используя выданный код разрезов графов.
  • Протестировать алгоритм на модельных данных.
  • Реализовать процедуру решения задачи стерео.
  • Подобрать унарные и парные потенциалы так, чтобы на выданных стереопарах достигался хороший (относительно истинных смещений) результат. Набор унарных и парных потенциалов, а также их параметров может быть своим для каждой стереопары.
  • На нескольких стереопарах из предыдущего пункта сравнить работу алгоритмов α-расширение и αβ-замена. Реализацию недостающего алгоритма можно взять у товарища, выполняющего другой вариант (в отчете обязательно указывать, чей код вы используете). Требуется провести сравнение по энергии получаемого решения, по времени работы, по визуальному качеству решения. Все выводы должны быть подтверждены числами, графиками, картинками.
  • Написать отчет в формате PDF с описанием всех проведенных исследований.

Спецификация реализуемых функций

Алгоритм
[labels, energy, time] = alphaExpansionGridPotts(unary, vertC, horC, metric)
[labels, energy, time] = alphaExpansionGridPotts(unary, vertC, horC, metric, options)
[labels, energy, time] = alphaBetaSwapGridPotts(unary, vertC, horC, metric)
[labels, energy, time] = alphaBetaSwapGridPotts(unary, vertC, horC, metric, options)
ВХОД
unary — унарные потенциалы, массив типа double размера N x M x K, где N — высота решетки, M — ширина решетки, K — количество меток.
vertC — коэффициенты c_{pq}, соответствующие вертикальным ребрам, массив типа double размера (N — 1) x M;
horC — коэффициенты c_{pq}, соответствующие горизонтальным ребрам, массив типа double размера N x (M — 1);
metric - расстояние между метками соседних переменных, массив типа double размера K x K;
options — (необязательный аргумент) набор дополнительных параметров, структура с полями
  'maxIter' — максимально допустимое число итераций алгоритма (по умолчанию = 500);
  'display' — параметр типа logical: если true, то при каждом запуске алгоритма разреза графа нужно выводить на экран номер итерации, номера обрабатываемых меток, текущее значение энергии;
  'numStart' — количество запусков из разных начальных приближений;
  'randOrder' — параметр типа logical: если true, то при каждом запуске использовать случайный порядок меток α и β;
ВЫХОД
labels — разметка, обладающая наименьшей энергией, массив типа double размера N x M;
energy — значения энергии на каждой итерации, вектор типа double длины, равной количеству итераций алгоритма;
time — время, пройденное с начала работы алгоритма до каждой итерации, вектор типа double длины, равной количеству итераций алгоритма;

Обратите внимание: в процедурах alphaExpansionGridPotts и alphaBetaSwapGridPotts параметры N, M, и K определяются неявно по размеру соответствующих элементов.

Стерео
[disparity] = stereo(name)
ВХОД
name — название стерео пары, строка.
ВЫХОД
disparity — массив смещений массив типа double размера N x M со значениями -∞,...,∞.

В каталоге, из которого будет запускаться решение при проверке, будет лежать выданный каталог datasets.

Рекомендации по выполнению задания

  1. Обратите внимание на область применимости алгоритма.
  2. При тестировании алгоритма необходимо следить за следующим:
    • после каждого применения разреза графа общая энергия не возрастает;
    • значение энергии, выдаваемое функцией graphCutMex, совпадает со значением энергии, подсчитанным независимой процедурой.
  3. Потенциалы для стереопары tsukuba и примеры работы различных алгоритмов: http://vision.middlebury.edu/MRF/results/tsukuba/index.html

Данные для выполнения задания

graphCut — MATLAB интерфейс к разрезам графов.

rgb2luv — конвертер изображений в формат YUV.

datasets — стереопары.

Оформление задания

Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «[ГМ13] задание 4, вариант X, фамилия». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.

Письмо должно содержать:

  • PDF-файл с описанием проведенных исследований (отчет должен включать в себя описание выполнения каждого пункта задания с приведением соответствующих графиков, изображений, чисел)
  • Все исходные файлы, реализованные в рамках настоящего задания. Убедитесь, что Ваши файлы работают и соответствуют прототипам!
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%93%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2013/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_4»