БММО (курс лекция)/2013/Задание 2

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Модель Изинга)
Строка 188: Строка 188:
*На этапе тестирования функций рекомендуется проводить эксперименты со случайным внешним магнитным полем <tex>H</tex>.
*На этапе тестирования функций рекомендуется проводить эксперименты со случайным внешним магнитным полем <tex>H</tex>.
*Одной из возможных проверок на корректность оценки статистик по сгенерированному набору конфигураций <tex>X</tex>
*Одной из возможных проверок на корректность оценки статистик по сгенерированному набору конфигураций <tex>X</tex>
 +
 +
== Вариант 2 ==
 +
 +
=== Описание задания ===
 +
 +
Провести исследование модели Изинга с помощью вариационного подхода, где в качестве факторизованного семейства для <tex>q(X)</tex> выступает независимое распределение по всем компонентам <tex>x_i</tex>:<br>
 +
<tex>
 +
q(X)=\prod_{i=1}^Nq_i(x_i).
 +
</tex>
 +
 +
Необходимые формулы пересчета для вариационного подхода:<br>
 +
<tex>
 +
b_i = H_i + J\sum_{j:(i,j) \in\mathcal{E}}\mathbb{E}x_j,
 +
</tex><br>
 +
<tex>
 +
q_i(x_i = 1) = \frac{1}{1 + \exp(-2\beta b_i)},
 +
</tex><br>
 +
<tex>
 +
\mathbb{E}x_i = 2q_i(x_i=1)-1.
 +
</tex>
 +
 +
При этом нижняя граница на значение логарифма нормировочной константы <tex>\log Z</tex> равна<br>
 +
<tex>
 +
\mathcal{L}(q) = \beta\left(\sum_{i=1}^NH_i\mathbb{E}x_i + \frac{J}{2}\sum_{(i,j)\in\mathcal{E}}\mathbb{E}x_i\mathbb{E}x_j\right) - \sum_{i=1}^N\left[q_i(x_i=1)\log(q_i(x_i=1)) + (1-q_i(x_i=1))\log(1-q_i(x_i=1))\right].
 +
</tex>
 +
 +
Необходимые статистики для приближенного распределения <tex>q(X)</tex> вычисляются следующим образом:<br>
 +
<tex>
 +
\frac{1}{N}\mathbb{E}E = -\frac{1}{N}\left(\sum_{i=1}^NH_i\mathbb{E}x_i + \frac{J}{2}\sum_{(i,j)\in \mathcal{E}}\mathbb{E}x_i\mathbb{E}x_j\right),
 +
</tex>
 +
<br><tex>
 +
\mathbb{E}E^2 = \sum_{i,j=1}^NH_iH_j\mathbb{E}(x_ix_j) + J\sum_{n,(i,j)\in \mathcal{E}}H_n\mathbb{E}(x_nx_ix_j) + \frac{J^2}{4}\sum_{(i,j)\in\mathcal{E}, (n,m)\in\mathcal{E}}\mathbb{E}(x_ix_jx_nx_m),
 +
</tex>
 +
<br><tex>
 +
\mathbb{D}E = \mathbb{E}E^2 - (\mathbb{E}E)^2,
 +
</tex>
 +
<br><tex>
 +
\mathbb{E}\left(\sum_{i=1}^Nx_i\right)^2 = \sum_{i,j=1}^N\mathbb{E}(x_ix_j),
 +
</tex>
 +
<br><tex>
 +
\mathbb{E}x_ix_j = \mathbb{E}x_i\mathbb{E}x_j,\ i\neq j;\ \mathbb{E}x_i^2 = 1.
 +
</tex>
 +
 +
=== Задание ===
 +
# Вывести все необходимые формулы для вариационного подхода (вывод вставить в отчет).
 +
# Реализовать процедуру подсчета математического ожидания и дисперсии энергии (нормированной на количество спинов N), математического ожидания квадрата общей намагниченности модели <tex>\mu = \left(\sum_{i=1}^N x_i \right) / N</tex> с помощью вариационного подхода для заданных параметров <tex>\beta</tex> и внешнего магнитного поля H. (Требования по эффективности реализации для 3-ого курса и выше: для решетки размера 20 x 20 сто итераций поиска вариационного приближения для ста значений параметра <tex>\beta</tex> должны выполнятся не более одной секунды, включая этап оценки всех статистик. В отчете привести соответствующие замеры времени работы кода.)
 +
# Построить графики зависимости <tex>\frac{1}{N}\mathbb{E}E, \frac{1}{N}\sqrt{\mathbb{D}E}, \sqrt{\mathbb{E}(\mu^2)}, \mathcal{L}(q)</tex> от температуры для треугольной и четырехугольной систем соседства, ферромагнетика и антиферромагнетика (всего 4 модели). Проинтерпретировать полученные результаты (в частности идентифицировать, локализовать и изучить фазовый переход). Для построения графиков использовать следующие значения параметров:
 +
#*размер решетки 20 на 20 (N = 400);
 +
#*<tex>k = 1</tex>;
 +
#*для ферромагнетика <tex>J = 1</tex>, для антиферромагнетика <tex>J = -1</tex>;
 +
#*внешнее магнитное поле <tex>H_i = 0</tex>;
 +
#*температуры T = 0.5 : 0.1 : 10;
 +
#*количество итераций = 300;
 +
#*точность по значению нижней границы <tex>\mathcal{L}(q)</tex> = <tex>10^{-4}</tex> (останавливаем итерационный процесс, если значение <tex>\mathcal{L}(q)</tex> на текущей итерации изменилось меньше, чем на <tex>10^{-4}</tex>).
 +
#Исследовать влияние константного внешнего магнитного поля на фазовый переход в ферромагнетике с прямоугольной системой соседства. Привести соответствующие графики. Параметры модели взять такие же, как в пункте 3.
 +
#Сравнить результаты применения вариационного подхода с аналогичными для схемы Гиббса. Рассмотреть ферромагнетик с прямоугольной системой соседства. Реализацию схемы Гиббса взять у товарища, выполняющего вариант 1. Привести графики математического ожидания и дисперсии энергии, корня из математического ожидания намагниченности в одних осях для двух подходов. Убедиться в том, что <tex>\mathcal{L}</tex> является нижней границей для логарифма нормировочной константы, полученного с помощью схемы Гиббса.
 +
 +
=== Оформление задания ===
 +
 +
Выполненное задание следует отправить письмом по адресу ''bayesml@gmail.com'' с заголовком письма «Задание 3 <Номер_группы> <ФИО>». Убедительная просьба присылать выполненное задание '''только один раз''' с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также большая просьба строго следовать указанным ниже прототипам реализуемых функций.
 +
 +
Программная среда для выполнения задания — MATLAB.
 +
 +
Присланный вариант задания должен содержать в себе:
 +
* ФИО исполнителя, номер группы и номер варианта задания.
 +
* Текстовый файл в формате PDF, содержащий описание проведенных исследований.
 +
* Все исходные коды с необходимыми комментариями.
 +
* Дополнительные комментарии или материалы, если необходимо.
 +
 +
Исходные коды должны включать в себя реализацию вариационного подхода для прямоугольной и треугольной систем соседств в виде отдельных функций (отдельных m-файлов). Прототипы функций имеют следующий вид:<br>
 +
{|class="standard"
 +
!''Вариационный подход''
 +
|-
 +
|[E, D, M, L] = varIsing4(H, J, betaAll, opt_params) — прямоугольная система соседства
 +
|-
 +
|[E, D, M, L] = varIsing6(H, J, betaAll, opt_params) — треугольная система соседства
 +
|-
 +
|ВХОД
 +
|-
 +
|
 +
{|border="0"
 +
|-
 +
|H — внешнее магнитное поле, матрица размера vS x hS;
 +
|-
 +
|J — параметр модели J;
 +
|-
 +
|betaAll — вектор значений параметра <tex>\beta</tex> (в MatLab матрица размера 1 x <tex>\beta_0</tex>);
 +
|-
 +
|opt_params — (необязательный параметр) параметры оптимизационного процесса, структура со следующими полями:
 +
{|border="0"
 +
|'max_iter' — максимальное количество итераций, по умолчанию = 300;
 +
|-
 +
|'tol_crit' — необходимая точность по значению нижней границы, по умолчанию = <tex>10^{-4}</tex>;
 +
|-
 +
|'num_start' — количество различных начальных приближений, по умолчанию = 1;
 +
|}
 +
|}
 +
|-
 +
|ВЫХОД
 +
|-
 +
|
 +
{|
 +
|E — мат.ожидание энергии на один спин <tex>\frac{1}{N}\mathbb{E}E</tex> для каждой температуры, массив размера 1 x <tex>\beta_0</tex>;
 +
|-
 +
|D — стандартное отклонение энергии на один спин <tex>\frac{1}{N}\sqrt{\mathbb{D}E}</tex> для каждой температуры, массив размера 1 x <tex>\beta_0</tex>;
 +
|-
 +
|M — средняя магнетизация <tex>\sqrt{\mathbb{E}\mu^2}</tex> для каждой температуры, массив размера 1 x <tex>\beta_0</tex>;
 +
|-
 +
|L — нижние границы для логарифмов нормировочных констант для каждой температуры, массив размера 1 x <tex>\beta_0</tex>.
 +
|-
 +
|}
 +
|}
 +
 +
=== Рекомендации ===
 +
*Рекомендуется реализовывать метод с векторными операциями по параметру <tex>\beta</tex>, т.е. проводить вычисления для всех температур сразу.
 +
*Рекомендуется запускать вариационную оптимизацию из нескольких начальных приближений для <tex>q</tex>: случайные, все вероятности одинаковые и близки к единице, шахматная доска и т.д. При этом для текущей температуры наилучшим вариационным приближением признается такое, при котором значение нижней границы <tex>\mathcal{L}(q)</tex> является максимальным.
 +
*Одной из проверок на корректность оптимизации в рамках вариационного подхода является монотонное возрастание значения нижней границы <tex>\mathcal{L}(q)</tex>.
 +
*На этапе тестирования функций рекомендуется проводить эксперименты со случайным внешним магнитным полем <tex>H</tex>.
 +
*Одной из возможных проверок на корректность вычисления различных статистик по приближению <tex>q</tex> является использование метода Монте Карло, при котором генерируется набор конфигураций <tex>X^j</tex> (каждая конфигурация состоит из независимых спинов <tex>x_i^j</tex>), по которым затем оцениваются необходимые статистики.

Версия 20:55, 23 апреля 2013

Содержание


Основная статья: Байесовские методы машинного обучения (курс лекций, Д.П. Ветров, Д.А. Кропотов)

Начало выполнения задания: 30 апреля 2013 г.
Срок сдачи: 14 мая 2013 г. (вторник), 23:59.

Модель Изинга

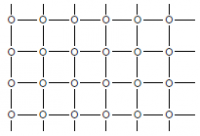
Прямоугольная система соседства
Прямоугольная система соседства
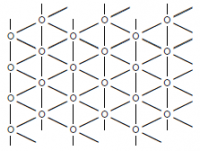
Треугольная система соседства
Треугольная система соседства

Модель Изинга — математическая модель статистической физики, предназначенная для описания магнитных свойств вещества. Каждой вершине кристаллической решётки (рассматривается двухмерный случай) сопоставляется число, называемое спином и равное +1 или −1 («поле вверх»/«поле вниз»). Каждому из 2^N возможных вариантов расположения спинов (где N — число атомов решётки) приписывается энергия, состоящая из взаимодействия спинов соседних атомов J и действия внешнего магнитного поля H:
E(X) = -\left( \frac{J}{2} \sum_{(i,j) \in\mathcal{E}} x_i x_j + \sum_{i=1}^N H_i x_i \right),
где x_i — переменные, соответствующие спинам, \mathcal{E{ — система соседства (в данном задании рассматриваются две системы соседства: прямоугольная и треугольная). Пара (i,j)\in\mathcal{E} не является упорядоченной. Вероятность нахождения в каждом конкретном состоянии задается распределением Гиббса:
P(X) = \frac{1}{Z} \exp{\left( -\beta E(X) \right)}, \qquad \beta = \frac{1}{kT},
где Z — нормировочная константа, T — температура, k — параметр.

Если J = 1 , то вещество называется ферромагнетиком. Если J = -1, то вещество называется антиферромагнетиком.

Задание состоит из двух вариантов. Распределение по вариантам:

№ п/п Студент Вариант Оценка
1 Шальнов 1
2 Чистяков 2
3 Захаров 1
4 Козлов 2
5 Апишев 1
6 Шишватов 2
7 Максимов 1
8 Хальман 2
9 Чурьянов 1
10 Кольцов 1
11 Вашуров 2
12 Колосов 2
13 Николайчук 1
14 Хомутов 2
15 Готман 2
16 Ожерельев 1
17 Сокурский 1
18 Новиков 2
18 Таболин 1

Кто не обнаружил себя в списках, пожалуйста, отпишитесь нам (bayesml@gmail.com). Если чью-то фамилию не разобрал, не взыщите - сообщите и мы исправим :) Для студентов второго курса требования по эффективности реализации являются опциональными.

Вариант 1

Описание задания

Провести исследование модели Изинга методом Монте-Карло по схеме Гиббса. В этой схеме генерация значения очередного элемента решетки x_i производится по следующим формулам:
p(x_i = 1 | X_{/\{i\}}) = \frac{1}{1 + \exp(-2\beta b_i)}, \qquad b_i = J\sum_{j: (i, j) \in\mathcal{E}} x_j + H_i,
p(x_i = -1 | X_{/\{i\}}) = \frac{\exp(-2\beta b_i)}{1 + \exp(-2\beta b_i)}.

Задание

Пример иллюстрации состояния модели Изинга размера 20 на 20.
Пример иллюстрации состояния модели Изинга размера 20 на 20.
  1. Вывести формулы генерации выборки по схеме Гиббса из модели Изинга (вывод вставить в отчет).
  2. Вывести формулу для w_m в методе оценки нормировочной константы по схеме Гиббса для модели Изинга через рассмотрение промежуточных распределений, начиная с равномерного (вывод вставить в отчет).
  3. Реализовать процедуру подсчета математического ожидания и дисперсии энергии (нормированной на количество спинов N), математического ожидания квадрата общей намагниченности модели \mu = \left(\sum_{i=1}^N x_i \right) / N методом Гиббса (с заданным числом итераций) для заданных параметров \beta и внешнего магнитного поля H. (Требования по эффективности реализации для 3-ого курса и выше: 1000 итераций метода Гиббса для решетки размера 20 на 20 и ста значений параметра \beta должны выполняться не более 20 секунд. В отчете привести соответствующие замеры времени работы кода.)
  4. Реализовать процедуру оценки логарифма нормировочной константы распределения \log(Z) для модели Изинга с помощью схемы Гиббса и набора промежуточных распределений, начиная с равномерного.
  5. Построить графики зависимости \frac{1}{N}\mathbb{E}E, \frac{1}{N}\sqrt{\mathbb{D}E}, \sqrt{\mathbb{E}(\mu^2)}, \log(Z) от температуры для треугольной и четырехугольной систем соседства, ферромагнетика и антиферромагнетика (всего 4 модели). Проинтерпретировать полученные результаты (в частности идентифицировать, локализовать и изучить фазовый переход). Для построения графиков использовать следующие значения параметров:
    • размер решетки 20 на 20 (N = 400);
    • k = 1;
    • 10000 итераций метода Гиббса для оценки статистик, 50 итераций для оценки нормировочных констант;
    • 1000 промежуточных распределений для оценки нормировочных констант.
    • для ферромагнетика J = 1, для антиферромагнетика J = -1;
    • внешнее магнитное поле H_i = 0;
    • температуры T = 0.5 : 0.1 : 10.
  6. Для ферромагнетика с четырехугольной системой связности отобразить характерные отдельные конфигурации X (см. рис.) в зависимости от температуры (низкая температура, окрестность фазового перехода, высокая температура). Проинтерпретировать результаты. Рассмотреть как минимум по одному примеру для не менее, чем пяти разных значений температур. Параметры генерации те же, что и в пункте 5.
  7. Исследовать влияние константного внешнего магнитного поля на фазовый переход в ферромагнетике с прямоугольной системой соседства. Привести соответствующие графики. Параметры модели взять такие же, как в пункте 5.
  8. Выполнить пункт 6 в присутствии внешнего магнитного поля со следующей структурой: на половине решетки H = 1, на другой половине H = -1.
  9. Сравнить результаты метода Монте-Карло с результатами вариационного подхода. Рассмотреть ферромагнетик с прямоугольной системой соседства. Реализацию вариационного подхода взять у товарища, выполняющего вариант 2. Привести графики математического ожидания и дисперсии энергии, корня из математического ожидания намагниченности в одних осях для двух подходов. Убедиться, что оценка логарифма нормировочной константы по схеме Гиббса является верхней оценкой для \mathcal{L}(q) в вариационном подходе.

Оформление задания

Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «Задание 3 <Номер_группы> <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также большая просьба строго следовать указанным ниже прототипам реализуемых функций.

Программная среда для выполнения задания — MATLAB.

Присланный вариант задания должен содержать в себе:

  • ФИО исполнителя, номер группы и номер варианта задания.
  • Текстовый файл в формате PDF, содержащий описание проведенных исследований.
  • Все исходные коды с необходимыми комментариями.
  • Дополнительные комментарии или материалы, если необходимо.

Исходные коды должны включать в себя реализацию метода Гиббса для прямоугольной и треугольной систем соседств в виде отдельных функций (отдельных m-файлов). Прототипы функций имеют следующий вид:

Метод Гиббса для оценки статистик распределений
[E, D, M, S] = gibbsIsing4(H, J, betaAll, num_iter) — прямоугольная система соседства
[E, D, M, S] = gibbsIsing6(H, J, betaAll, num_iter) — треугольная система соседства
ВХОД
H — внешнее магнитное поле, матрица типа double размера vS x hS;
J — параметр модели J;
betaAll — вектор значений параметра \beta (в MatLab матрица типа double размера 1 x \beta_0);
num_iter — количество итераций схемы Гиббса;
ВЫХОД
E — значения мат.ожиданий энергии на один спин \frac{1}{N}\mathbb{E}E для каждой температуры, массив размера 1 x \beta_0;
D — значения стандартных отклонений энергии на один спин \frac{1}{N}\sqrt{\mathbb{D}E} для каждой температуры, массив размера 1 x \beta_0;
M — значения средней магнетизации на один спин \mathbb{E}\mu^2 для каждой температуры, массив размера 1 x \beta_0;
S — примеры конфигураций X для всех температур, массив размера vS x hS x \beta_0.

 

Метод Гиббса для оценки нормировочных констант распределений
logZ = ZgibbsIsing4(H, J, betaAll, num_pdfs, num_iter) — прямоугольная система соседства
logZ = ZgibbsIsing6(H, J, betaAll, num_pdfs, num_iter) — треугольная система соседства
ВХОД
H — внешнее магнитное поле, матрица типа double размера vS x hS;
J — параметр модели J;
betaAll — вектор значений параметра \beta (в MatLab матрица типа double размера 1 x \beta_0);
num_pdfs — количество промежуточных распределений;
num_iter — общее число итераций;
ВЫХОД
logZ — значения логарифма нормировочных констант для каждой температуры, массив размера 1 x \beta_0.

Рекомендации

  • Рекомендуется реализовывать метод Гиббса с векторными операциями по параметру \beta, т.е. проводить вычисления для всех температур сразу.
  • Для оценки статистик распределения следует отбрасывать значения, полученные на первой трети итераций метода Гиббса.
  • В качестве примеров конфигураций X лучше брать ситуации с последних итераций схемы Гиббса.
  • На этапе тестирования функций рекомендуется проводить эксперименты со случайным внешним магнитным полем H.
  • Одной из возможных проверок на корректность оценки статистик по сгенерированному набору конфигураций X

Вариант 2

Описание задания

Провести исследование модели Изинга с помощью вариационного подхода, где в качестве факторизованного семейства для q(X) выступает независимое распределение по всем компонентам x_i:
q(X)=\prod_{i=1}^Nq_i(x_i).

Необходимые формулы пересчета для вариационного подхода:
b_i = H_i + J\sum_{j:(i,j) \in\mathcal{E}}\mathbb{E}x_j,
q_i(x_i = 1) = \frac{1}{1 + \exp(-2\beta b_i)},
\mathbb{E}x_i = 2q_i(x_i=1)-1.

При этом нижняя граница на значение логарифма нормировочной константы \log Z равна
\mathcal{L}(q) = \beta\left(\sum_{i=1}^NH_i\mathbb{E}x_i + \frac{J}{2}\sum_{(i,j)\in\mathcal{E}}\mathbb{E}x_i\mathbb{E}x_j\right) - \sum_{i=1}^N\left[q_i(x_i=1)\log(q_i(x_i=1)) + (1-q_i(x_i=1))\log(1-q_i(x_i=1))\right].

Необходимые статистики для приближенного распределения q(X) вычисляются следующим образом:
\frac{1}{N}\mathbb{E}E = -\frac{1}{N}\left(\sum_{i=1}^NH_i\mathbb{E}x_i + \frac{J}{2}\sum_{(i,j)\in \mathcal{E}}\mathbb{E}x_i\mathbb{E}x_j\right),
\mathbb{E}E^2 = \sum_{i,j=1}^NH_iH_j\mathbb{E}(x_ix_j) + J\sum_{n,(i,j)\in \mathcal{E}}H_n\mathbb{E}(x_nx_ix_j) + \frac{J^2}{4}\sum_{(i,j)\in\mathcal{E}, (n,m)\in\mathcal{E}}\mathbb{E}(x_ix_jx_nx_m),
\mathbb{D}E = \mathbb{E}E^2 - (\mathbb{E}E)^2,
\mathbb{E}\left(\sum_{i=1}^Nx_i\right)^2 = \sum_{i,j=1}^N\mathbb{E}(x_ix_j),
\mathbb{E}x_ix_j = \mathbb{E}x_i\mathbb{E}x_j,\ i\neq j;\ \mathbb{E}x_i^2 = 1.

Задание

  1. Вывести все необходимые формулы для вариационного подхода (вывод вставить в отчет).
  2. Реализовать процедуру подсчета математического ожидания и дисперсии энергии (нормированной на количество спинов N), математического ожидания квадрата общей намагниченности модели \mu = \left(\sum_{i=1}^N x_i \right) / N с помощью вариационного подхода для заданных параметров \beta и внешнего магнитного поля H. (Требования по эффективности реализации для 3-ого курса и выше: для решетки размера 20 x 20 сто итераций поиска вариационного приближения для ста значений параметра \beta должны выполнятся не более одной секунды, включая этап оценки всех статистик. В отчете привести соответствующие замеры времени работы кода.)
  3. Построить графики зависимости \frac{1}{N}\mathbb{E}E, \frac{1}{N}\sqrt{\mathbb{D}E}, \sqrt{\mathbb{E}(\mu^2)}, \mathcal{L}(q) от температуры для треугольной и четырехугольной систем соседства, ферромагнетика и антиферромагнетика (всего 4 модели). Проинтерпретировать полученные результаты (в частности идентифицировать, локализовать и изучить фазовый переход). Для построения графиков использовать следующие значения параметров:
    • размер решетки 20 на 20 (N = 400);
    • k = 1;
    • для ферромагнетика J = 1, для антиферромагнетика J = -1;
    • внешнее магнитное поле H_i = 0;
    • температуры T = 0.5 : 0.1 : 10;
    • количество итераций = 300;
    • точность по значению нижней границы \mathcal{L}(q) = 10^{-4} (останавливаем итерационный процесс, если значение \mathcal{L}(q) на текущей итерации изменилось меньше, чем на 10^{-4}).
  4. Исследовать влияние константного внешнего магнитного поля на фазовый переход в ферромагнетике с прямоугольной системой соседства. Привести соответствующие графики. Параметры модели взять такие же, как в пункте 3.
  5. Сравнить результаты применения вариационного подхода с аналогичными для схемы Гиббса. Рассмотреть ферромагнетик с прямоугольной системой соседства. Реализацию схемы Гиббса взять у товарища, выполняющего вариант 1. Привести графики математического ожидания и дисперсии энергии, корня из математического ожидания намагниченности в одних осях для двух подходов. Убедиться в том, что \mathcal{L} является нижней границей для логарифма нормировочной константы, полученного с помощью схемы Гиббса.

Оформление задания

Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «Задание 3 <Номер_группы> <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также большая просьба строго следовать указанным ниже прототипам реализуемых функций.

Программная среда для выполнения задания — MATLAB.

Присланный вариант задания должен содержать в себе:

  • ФИО исполнителя, номер группы и номер варианта задания.
  • Текстовый файл в формате PDF, содержащий описание проведенных исследований.
  • Все исходные коды с необходимыми комментариями.
  • Дополнительные комментарии или материалы, если необходимо.

Исходные коды должны включать в себя реализацию вариационного подхода для прямоугольной и треугольной систем соседств в виде отдельных функций (отдельных m-файлов). Прототипы функций имеют следующий вид:

Вариационный подход
[E, D, M, L] = varIsing4(H, J, betaAll, opt_params) — прямоугольная система соседства
[E, D, M, L] = varIsing6(H, J, betaAll, opt_params) — треугольная система соседства
ВХОД
H — внешнее магнитное поле, матрица размера vS x hS;
J — параметр модели J;
betaAll — вектор значений параметра \beta (в MatLab матрица размера 1 x \beta_0);
opt_params — (необязательный параметр) параметры оптимизационного процесса, структура со следующими полями:
'max_iter' — максимальное количество итераций, по умолчанию = 300;
'tol_crit' — необходимая точность по значению нижней границы, по умолчанию = 10^{-4};
'num_start' — количество различных начальных приближений, по умолчанию = 1;
ВЫХОД
E — мат.ожидание энергии на один спин \frac{1}{N}\mathbb{E}E для каждой температуры, массив размера 1 x \beta_0;
D — стандартное отклонение энергии на один спин \frac{1}{N}\sqrt{\mathbb{D}E} для каждой температуры, массив размера 1 x \beta_0;
M — средняя магнетизация \sqrt{\mathbb{E}\mu^2} для каждой температуры, массив размера 1 x \beta_0;
L — нижние границы для логарифмов нормировочных констант для каждой температуры, массив размера 1 x \beta_0.

Рекомендации

  • Рекомендуется реализовывать метод с векторными операциями по параметру \beta, т.е. проводить вычисления для всех температур сразу.
  • Рекомендуется запускать вариационную оптимизацию из нескольких начальных приближений для q: случайные, все вероятности одинаковые и близки к единице, шахматная доска и т.д. При этом для текущей температуры наилучшим вариационным приближением признается такое, при котором значение нижней границы \mathcal{L}(q) является максимальным.
  • Одной из проверок на корректность оптимизации в рамках вариационного подхода является монотонное возрастание значения нижней границы \mathcal{L}(q).
  • На этапе тестирования функций рекомендуется проводить эксперименты со случайным внешним магнитным полем H.
  • Одной из возможных проверок на корректность вычисления различных статистик по приближению q является использование метода Монте Карло, при котором генерируется набор конфигураций X^j (каждая конфигурация состоит из независимых спинов x_i^j), по которым затем оцениваются необходимые статистики.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%91%D0%9C%D0%9C%D0%9E_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D1%8F%29/2013/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_2»
Личные инструменты