Метод наименьших углов (пример)
Материал из MachineLearning.
м (→Выполнение алгоритма) |
|||
| (6 промежуточных версий не показаны.) | |||
| Строка 2: | Строка 2: | ||
алгоритм отбора признаков в задачах линейной [[регрессия|регрессии]]. | алгоритм отбора признаков в задачах линейной [[регрессия|регрессии]]. | ||
Алгоритм предложили Бредли Эфрон, Тревор Хасти и Роберт Тибширани | Алгоритм предложили Бредли Эфрон, Тревор Хасти и Роберт Тибширани | ||
| - | [http://stat.stanford.edu/ | + | [http://stat.stanford.edu/~imj/WEBLIST/2004/LarsAnnStat04.pdf]. |
LARS решает следующую задачу. Пусть назначена [[линейная регрессия (пример)|линейная регрессионная модель]]. | LARS решает следующую задачу. Пусть назначена [[линейная регрессия (пример)|линейная регрессионная модель]]. | ||
| Строка 9: | Строка 9: | ||
зависимой переменной. Также LARS предлагает метод оценки весов. | зависимой переменной. Также LARS предлагает метод оценки весов. | ||
| - | Алгоритм LARS похож на алгоритм [[шаговая регрессия|шаговой регрессии]]. Различие в том, что вместо последовательного добавления | + | Алгоритм LARS похож на алгоритм [[шаговая регрессия|шаговой регрессии]]. Различие в том, что алгоритм LARS, вместо последовательного добавления |
| - | свободных, на каждом шаге | + | свободных переменных, на каждом шаге изменяет их веса. Веса увеличиваются так, чтобы доставить наибольшую корреляцию |
с вектором [[анализ регрессионных остатков|регрессионных остатков]]. | с вектором [[анализ регрессионных остатков|регрессионных остатков]]. | ||
Основным достоинством LARS является то, что он выполняется за число шагов, не превышающее число свободных переменных. | Основным достоинством LARS является то, что он выполняется за число шагов, не превышающее число свободных переменных. | ||
| Строка 18: | Строка 18: | ||
Задана выборка - матрица <tex>X</tex>, столбцы которой соответствуют независимым переменным, а строки - элементам выборки и вектор <tex>\mathbf{y}</tex>, | Задана выборка - матрица <tex>X</tex>, столбцы которой соответствуют независимым переменным, а строки - элементам выборки и вектор <tex>\mathbf{y}</tex>, | ||
| - | содержащий элементы | + | содержащий элементы зависимой переменной. Назначена линейная модель <tex>\mathbf{y}=X\mathbf{\beta}+\mathbf{\varepsilon}</tex>. |
Обозначим множество столбцов матрицы <tex>X</tex> как <tex>\{\mathbf{x}_1,\ldots,\mathbf{x}_n\}</tex>. | Обозначим множество столбцов матрицы <tex>X</tex> как <tex>\{\mathbf{x}_1,\ldots,\mathbf{x}_n\}</tex>. | ||
Пусть выполнены условия нормировки | Пусть выполнены условия нормировки | ||
| - | <center><tex> \|\mathbf{y}\|_1=0, </tex> <tex> \|\mathbf{x}_j\|_1=0, </tex> <tex>\|\mathbf{x}_j\|_2^2= | + | <center><tex> \|\mathbf{y}\|_1=0, </tex> <tex> \|\mathbf{x}_j\|_1=0, </tex> <tex>\|\mathbf{x}_j\|_2^2=1, </tex> где <tex> j=1,\ldots,n.</tex></center> |
Предполагается, что векторы <tex>\mathbf{x}_1,\ldots,\mathbf{x}_n</tex> линейно независимы. | Предполагается, что векторы <tex>\mathbf{x}_1,\ldots,\mathbf{x}_n</tex> линейно независимы. | ||
| Строка 47: | Строка 47: | ||
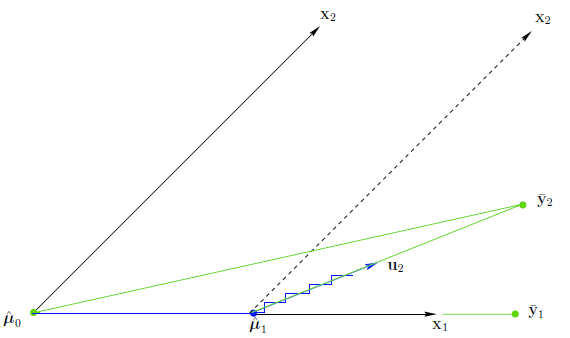
Скаляр <tex>\gamma_1</tex> выбирается таким образом, что вектор остатков <tex>\bar{\mathbf{y}}_2-\hat{\mathbf{\mu}}_0</tex> | Скаляр <tex>\gamma_1</tex> выбирается таким образом, что вектор остатков <tex>\bar{\mathbf{y}}_2-\hat{\mathbf{\mu}}_0</tex> | ||
делит пополам угол между векторами <tex>\mathbf{x}_1</tex> и <tex>\mathbf{x}_2</tex>. Далее получаем значение <tex>\hat{\mathbf{\mu}}_2=\hat{\mathbf{\mu}}_1+\gamma_2\mathbf{u}_2</tex>, | делит пополам угол между векторами <tex>\mathbf{x}_1</tex> и <tex>\mathbf{x}_2</tex>. Далее получаем значение <tex>\hat{\mathbf{\mu}}_2=\hat{\mathbf{\mu}}_1+\gamma_2\mathbf{u}_2</tex>, | ||
| - | где <tex>\mathbf{u}_2</tex> - | + | где <tex>\mathbf{u}_2</tex> - нормированный вектор, делящий этот угол пополам. |
Так как мы рассматриваем случай двух переменных, то | Так как мы рассматриваем случай двух переменных, то | ||
<tex>\hat{\mathbf{\mu}}_2=\bar{\mathbf{y}}_2</tex>. | <tex>\hat{\mathbf{\mu}}_2=\bar{\mathbf{y}}_2</tex>. | ||
| Строка 54: | Строка 54: | ||
На <tex>k</tex>-м шаге новое значение приближения вектора значений зависимой переменной <tex>\mathbf{y}</tex> вычисляется как | На <tex>k</tex>-м шаге новое значение приближения вектора значений зависимой переменной <tex>\mathbf{y}</tex> вычисляется как | ||
<center><tex>\hat{\mathbf{\mu}}_k=\hat{\mathbf{\mu}}_{k-1}+\gamma_k\mathbf{u}_k.</tex></center> | <center><tex>\hat{\mathbf{\mu}}_k=\hat{\mathbf{\mu}}_{k-1}+\gamma_k\mathbf{u}_k.</tex></center> | ||
| - | Здесь <tex>\mathbf{u}_k</tex> - | + | Здесь <tex>\mathbf{u}_k</tex> - нормированный вектор, задающий биссектрису между добавляемым вектором — столбцом матрицы <tex>X</tex> и вектором регрссионных остатков. |
Он вычисляется следующим образом. Пусть <tex>\mathcal{A}</tex> - подмножество индексов <tex>\{1,\dots,n\}</tex> столбцов матрицы <tex>X</tex>. | Он вычисляется следующим образом. Пусть <tex>\mathcal{A}</tex> - подмножество индексов <tex>\{1,\dots,n\}</tex> столбцов матрицы <tex>X</tex>. | ||
| Строка 86: | Строка 86: | ||
<center><tex>\hat{\mathbf{\mu}}_{\mathcal{A_{+}}} = \hat{\mathbf{\mu}}_{\mathcal{A}} + \hat\gamma\mathbf{u}_{\mathcal{A}},</tex></center> | <center><tex>\hat{\mathbf{\mu}}_{\mathcal{A_{+}}} = \hat{\mathbf{\mu}}_{\mathcal{A}} + \hat\gamma\mathbf{u}_{\mathcal{A}},</tex></center> | ||
где | где | ||
| - | <center><tex>\hat\gamma = {\min_{j\in\mathcal{A}^c}}^{+}\lbrace\frac{\hat{C}-\hat | + | <center><tex>\hat\gamma = {\min_{j\in\mathcal{A}^c}}^{+}\lbrace\frac{\hat{C}-\hat c_j}{A_{\mathcal{A}}-a_j},\frac{\hat C + \hat c_j}{A_{\mathcal{A}}+a_j}\rbrace. </tex> (*)</center> |
Минимум берется по всем положительным значениям аргументов для каждого <tex>j</tex>. | Минимум берется по всем положительным значениям аргументов для каждого <tex>j</tex>. | ||
| Строка 111: | Строка 111: | ||
может быть добавлен в набор <tex>\mathcal{A}</tex>. | может быть добавлен в набор <tex>\mathcal{A}</tex>. | ||
| - | == | + | Для иллюстрации работы алгоритма задумаем модель |
| + | <tex>f = w_1+w_2\sqrt(x)+w_3x</tex> ([[Порождение линейных регрессионных моделей (постановка задачи)|более подробно см.]]). | ||
| + | <source lang="matlab"> | ||
| + | f = inline('w(1)*x.^0 + w(2)*x.^(1/2) + w(3)*x.^1', 'w','x'); % synthetic model | ||
| + | b = [1 -2 2]'; % parameters | ||
| + | x = [0.1:0.1:1]'; % independent variable | ||
| + | y = f(b,x); % dependent variable | ||
| + | </source> | ||
| + | Пусть имеется выборка, в которой вектор-столбцы матрицы <tex>X</tex> | ||
| + | <center><tex>X = \left( \begin{array}{ccccc} x^0_1 & \sqrt{x}_1 & x\sqrt{x}_1 & x_1 & x\log{x}_1 \\ \vdots& \vdots & \vdots &\vdots &\vdots \\ x^0_m & \sqrt{x}_m & x\sqrt{x}_m & x_1 & x\log{x}_m \\ \end{array} \right)</tex></center> | ||
| + | и вектор <tex>\mathbf{y}=(y_1,\ldots,y_m)</tex>. | ||
| + | <source lang="matlab"> | ||
| + | % We use the following features to find the model we thought of | ||
| + | g = {'x.^0', 'x.^(1/2)', 'x.^1', 'x.^(3/2)', 'x.*log(x)'}; | ||
| + | % make the sample set; columns are independent variables | ||
| + | X = eval([ '[' g{1} ' ' g{2} ' ' g{3} ' ' g{4} ' ' g{5} ']']); | ||
| + | </source> | ||
| + | Принята линейная модель <tex>\mathbf{y}=X\mathbf{\beta}</tex>. Требуется последовательно отобрать вектор-столбцы матрицы <tex>X</tex>, | ||
| + | которые имеют наибольшую корреляцию с вектором остатков. Алгоритм LARS в данном примере сделает <tex>n=5</tex> шагов. | ||
| + | <source lang="matlab"> | ||
| + | [n,p] = size(X); | ||
| + | muA = zeros(n,1); % estimation of the dependent variable | ||
| + | beta = zeros(p,1); % estimation of parameters | ||
| + | betaLtst = beta'; % keep parameters in a storage | ||
| + | |||
| + | for i = 1:p | ||
| + | % correlation coefficients between each feature (column of X) and vector of residuals | ||
| + | c = X'*(y-muA); % note that columns of X are centered and normalized | ||
| + | [C, A] = max(abs(c)); % find maximal value of correlation and corresponding index j of column in X | ||
| + | % A = find(C == abs(c)); | ||
| + | % Aplus = find(C==c); % never used | ||
| + | Sj = sign(c(A)); % get sign of j-th correlation coefficient | ||
| + | XA = X(:,A).*(ones(n,1)*Sj'); % | ||
| + | % XA = X(:,A)*Sj; % | ||
| + | G = XA'*XA; % norm of XA | ||
| + | oA = ones(1,length(A)); % vector of ones | ||
| + | AA =(oA*G^(-1)*oA')^(-0.5); % inverse matrix in the normal equation | ||
| + | |||
| + | wA = AA*G^(-1)*oA'; % parameters to compute the unit bisector | ||
| + | uA = XA*wA; % compute the unit bisector | ||
| + | a = X'*uA; % product vector to compute new gamma | ||
| + | if i<p % for all columns of X but the last | ||
| + | M = [(C-c)./(AA-a);(C+c)./(AA+a)]; | ||
| + | M(find(M<=0)) = +Inf; | ||
| + | gamma = min(M); | ||
| + | else | ||
| + | gamma = C/AA; | ||
| + | end | ||
| + | |||
| + | muA = muA + gamma*uA; % make new approximation of the dependent variable | ||
| + | beta(A) = beta(A) + gamma*wA.*Sj; % make new parameters | ||
| + | betaLtst = [betaLtst; beta']; % store the parameters at k-th step | ||
| + | end | ||
| + | </source> | ||
| + | |||
| + | Результатом работы алгоритма является последовательность добавляемых признаков (веса которых отличны от нуля). | ||
| + | 0.5739 0 0 0 0 | ||
| + | 0.5739 0.0311 0 0 0 | ||
| + | 0.5739 0.0311 0 0 0 | ||
| + | 0.5739 0.0439 0 0 0 | ||
| + | 0.5739 0.0439 0.2135 0 0 | ||
| + | |||
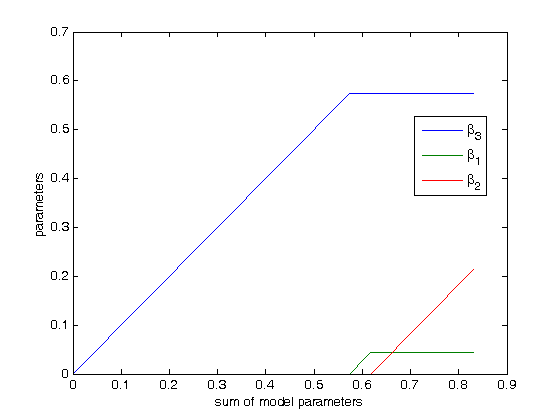
| + | [[Изображение:lars_parameters.png|frame|На графике показано изменение вектора параметров <tex>\mathbf{\beta}</tex> по шагам LARS. | ||
| + | По оси абсцисс отложена сумма параметров, по оси ординат - их значения. Согласно исходной модели, только первые три параметра отличны от нуля.]] | ||
| + | |||
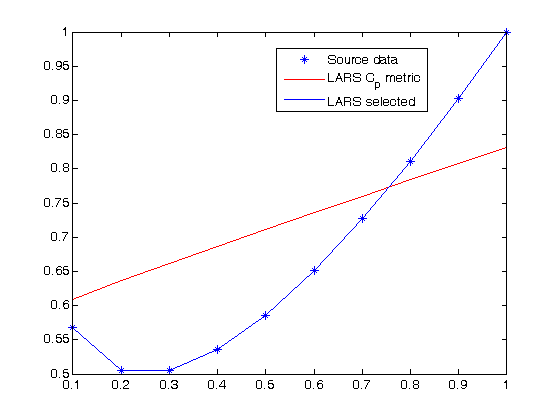
| + | [[Изображение:lars_model.png|frame|Ось абсцисс - свободная переменная, ось ординат - зависимая. Точками показаны исходные данные, | ||
| + | соответствующие задуманной модели. Красная линия - модель LARS с параметрами <tex>\mathbf{\beta}</tex>, полученными | ||
| + | с помощью LARS. Красная линия - модель для параметров, выбранных LARS и настроеных с помощью [[метод наименьших квадратов|метода наименьших квадратов]].]] | ||
== Литература == | == Литература == | ||
* Tibshirani R. Regression shrinkage and Selection via the Lasso. // Journal of the Royal Statistical Society.Series B(Metodological). 1996 Vol. 32, \No 1, p.267-288. | * Tibshirani R. Regression shrinkage and Selection via the Lasso. // Journal of the Royal Statistical Society.Series B(Metodological). 1996 Vol. 32, \No 1, p.267-288. | ||
* Efron B., Hastie T., Johnstone J., Tibshirani R. Least Angle Regression. // The Annals of Statistics, 2004. Vol. 32, \No 2, p. 407-499. | * Efron B., Hastie T., Johnstone J., Tibshirani R. Least Angle Regression. // The Annals of Statistics, 2004. Vol. 32, \No 2, p. 407-499. | ||
| - | |||
| - | |||
== См. также == | == См. также == | ||
Текущая версия
Метод наименьших углов (англ. least angle regression, LARS) - алгоритм отбора признаков в задачах линейной регрессии. Алгоритм предложили Бредли Эфрон, Тревор Хасти и Роберт Тибширани [1].
LARS решает следующую задачу. Пусть назначена линейная регрессионная модель. При большом количестве свободных переменных возникает проблема неустойчивого оценивания весов модели. LARS предлагает метод выбора такого набора свободных переменных, который имел бы наиболее значимую статистическую связь с зависимой переменной. Также LARS предлагает метод оценки весов.
Алгоритм LARS похож на алгоритм шаговой регрессии. Различие в том, что алгоритм LARS, вместо последовательного добавления свободных переменных, на каждом шаге изменяет их веса. Веса увеличиваются так, чтобы доставить наибольшую корреляцию с вектором регрессионных остатков. Основным достоинством LARS является то, что он выполняется за число шагов, не превышающее число свободных переменных. Частным случаем алгоритма LARS является алгоритм LASSO.
Содержание |
Постановка задачи
Задана выборка - матрица , столбцы которой соответствуют независимым переменным, а строки - элементам выборки и вектор
,
содержащий элементы зависимой переменной. Назначена линейная модель
.
Обозначим множество столбцов матрицы как
.
Пусть выполнены условия нормировки
Предполагается, что векторы линейно независимы.
Критерием качества модели назначена среднеквадратичная ошибка
Требуется найти для каждого шага LARS вектор весов и набор столбцов,
доставляющий наибольшую корреляцию векторов
и
.
Описание алгоритма
LARS последовательными шагами строит оценку коэффициентов .
На
-м шаге только
элементов вектора
отличны от нуля.
Алгоритм последовательно вычисляет приближение вектора значений зависимой переменной
Для приближений используется вектор корреляций столбцов матрицы с вектором остатков
На -м шаге новое значение приближения вектора значений зависимой переменной
вычисляется как
Здесь - нормированный вектор, задающий биссектрису между добавляемым вектором — столбцом матрицы
и вектором регрссионных остатков.
Он вычисляется следующим образом. Пусть - подмножество индексов
столбцов матрицы
.
Это подмножество задает подматрицу
где множитель и
- мощность множества
.
Обозначим ковариационную матрицу
где - вектор, состоящий из
единиц.
Вычислим единичный вектор
Вектор образует со столбцами матрицы
одинаковые углы, меньшие
.
Справедливы равенства
Выполнение алгоритма
Назначим начальную оценку вектора значений зависимой переменной .
Вычислим текущую оценку
и вектор корреляций
Найдем текущий набор индексов , соответствующих признакам с наибольшими абсолютными значениями корреляций
Пусть для
Построим матрицы
,
. Вычислим вектор
и вектор скалярных произведений
Пересчитаем значение вектора
где
Минимум берется по всем положительным значениям аргументов для каждого .
Алгоритм повторяется раз.
Замечание
Величина в формуле (*) интерпретируется следующим образом.
Определим
при условии . Корреляция по добавляемому
-му признаку равна
Для получаем
Это означает, что все рассматриваемые на данном шаге максимальные абсолютные корреляции уменьшаются на одну и ту же величину.
Из предыдущих двух соотношений мы видим,
что при корреляция
принимает наибольшее значение при
Аналогично, корреляция принимает наибольшее значение при
Таким образом, в выражении (*) - минимальная положительная величина, при которой новый индекс
может быть добавлен в набор
.
Для иллюстрации работы алгоритма задумаем модель
(более подробно см.).
f = inline('w(1)*x.^0 + w(2)*x.^(1/2) + w(3)*x.^1', 'w','x'); % synthetic model b = [1 -2 2]'; % parameters x = [0.1:0.1:1]'; % independent variable y = f(b,x); % dependent variable
Пусть имеется выборка, в которой вектор-столбцы матрицы
и вектор .
% We use the following features to find the model we thought of g = {'x.^0', 'x.^(1/2)', 'x.^1', 'x.^(3/2)', 'x.*log(x)'}; % make the sample set; columns are independent variables X = eval([ '[' g{1} ' ' g{2} ' ' g{3} ' ' g{4} ' ' g{5} ']']);
Принята линейная модель . Требуется последовательно отобрать вектор-столбцы матрицы
,
которые имеют наибольшую корреляцию с вектором остатков. Алгоритм LARS в данном примере сделает
шагов.
[n,p] = size(X); muA = zeros(n,1); % estimation of the dependent variable beta = zeros(p,1); % estimation of parameters betaLtst = beta'; % keep parameters in a storage for i = 1:p % correlation coefficients between each feature (column of X) and vector of residuals c = X'*(y-muA); % note that columns of X are centered and normalized [C, A] = max(abs(c)); % find maximal value of correlation and corresponding index j of column in X % A = find(C == abs(c)); % Aplus = find(C==c); % never used Sj = sign(c(A)); % get sign of j-th correlation coefficient XA = X(:,A).*(ones(n,1)*Sj'); % % XA = X(:,A)*Sj; % G = XA'*XA; % norm of XA oA = ones(1,length(A)); % vector of ones AA =(oA*G^(-1)*oA')^(-0.5); % inverse matrix in the normal equation wA = AA*G^(-1)*oA'; % parameters to compute the unit bisector uA = XA*wA; % compute the unit bisector a = X'*uA; % product vector to compute new gamma if i<p % for all columns of X but the last M = [(C-c)./(AA-a);(C+c)./(AA+a)]; M(find(M<=0)) = +Inf; gamma = min(M); else gamma = C/AA; end muA = muA + gamma*uA; % make new approximation of the dependent variable beta(A) = beta(A) + gamma*wA.*Sj; % make new parameters betaLtst = [betaLtst; beta']; % store the parameters at k-th step end
Результатом работы алгоритма является последовательность добавляемых признаков (веса которых отличны от нуля).
0.5739 0 0 0 0 0.5739 0.0311 0 0 0 0.5739 0.0311 0 0 0 0.5739 0.0439 0 0 0 0.5739 0.0439 0.2135 0 0
Литература
- Tibshirani R. Regression shrinkage and Selection via the Lasso. // Journal of the Royal Statistical Society.Series B(Metodological). 1996 Vol. 32, \No 1, p.267-288.
- Efron B., Hastie T., Johnstone J., Tibshirani R. Least Angle Regression. // The Annals of Statistics, 2004. Vol. 32, \No 2, p. 407-499.