Описание окрестности точки наибольшего правдоподобия моделей (пример)
Материал из MachineLearning.
(→Исходный код) |
|||
| (49 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
== Постановка задачи == | == Постановка задачи == | ||
| - | Пусть, | + | Пусть задана выборка <tex>D = \{(\mathbf{x}^i, y^i\)}</tex> из m пар. |
| - | <tex> | + | <tex>\{\mathbf{x}^i\}^m_{i=1}</tex> - множество из m объектов, |
| + | <tex>\mathbf{x}^i = [x^i_1, \ldots, x^i_n]^T \in\mathbb{R}^n</tex> , где n - количество признаков, а | ||
| + | <tex>y^i\in\mathbb{R}</tex> - соответствующая зависимая переменная. | ||
| - | <tex>\{ | + | <tex>\mathbf{x}_j = [x^1_j, \ldots, x^m_j]^T \in\mathbb{R}^m</tex> - вектор значений j-ого признака, а |
| + | <tex>\mathbf{y} = [y^1, \ldots, y^m]^T \in\mathbb{R}^m</tex> - вектор целевого признака. | ||
| - | |||
| + | <center><tex>D = ([\mathbf{x}_1, \ldots, \mathbf{x}_n], \mathbf{y}) = (X, \mathbf{y})</tex></center> | ||
| - | |||
| - | |||
| - | + | Пусть <tex>I = \{1, \ldots, m\}</tex> - множество индексов объектов, | |
| + | <tex>J = \{1, \ldots,n\}</tex> - множество индексов признаков. <tex>A\subseteq J</tex> - подмножество активных признаков. | ||
| + | Множество <tex>A</tex> задаёт регрессионную модель <tex>f_A</tex>, а <tex>c_f = |A|</tex> - сложность модели. | ||
| + | Рассмотрим следующую линейную модель регрессии, описывающую связь между свободными и зависимой переменными | ||
| + | |||
| + | <center><tex>\mathbf{y} = f_A(X, \mathbf{w}) + \mathbf{\varepsilon} = X \mathbf{w} + \mathbf{\varepsilon}</tex> , (1)</center> | ||
| + | |||
| + | |||
| + | где <tex>\mathbf{w} = [\ldots, w_j, \ldots]^T_{j\in A}</tex> - вектор параметров регрессии, а случайная аддитивная переменная <tex>\mathbf{\varepsilon}</tex> регрессионной модели имеет нормальное распределение | ||
| + | <tex>\varepsilon \in N(0, \sigma^2)</tex>. | ||
| + | |||
| + | |||
| + | Распределение зависимой переменной будет иметь следующий вид: | ||
| + | |||
| + | <center><tex>p(y|x, \mathbf{w}, \sigma^2, f) = \frac{exp(-\frac{1}{\sigma^2}S)}{(2\pi\sigma^2){\frac{n}{2}}},</tex></center> | ||
| + | |||
| + | |||
| + | где <tex>S</tex> - сумма квадратов невязок <tex>y^i - f(\mathbf{x}^i, \mathbf{w})</tex>. Согласно оценки точки наибольшего правдоподобия, данное распределение задаёт критерий качества модели, равный сумме квадратов регрессионных остатков. | ||
| + | |||
| + | <center><tex>S = \sum_{i\in \Theta} (y^i - f(\mathbf{x}^i, \mathbf{w}))^2</tex> , (2)</center> | ||
| + | |||
| + | |||
| + | где <tex>\Theta \subseteq I</tex> - некоторое множество индексов. Этот критерий используется при выборе модели в дальнейшем. | ||
| + | |||
| + | |||
| + | Мультиколлинеарность отслеживается с помощью фактора инфляции дисперсии (VIF), связанного с корреляцей данного признака с другими: | ||
| + | |||
| + | |||
| + | <center><tex>VIF_j = \frac{1}{1 - R_j^2}</tex> (3)</center> | ||
| + | |||
| + | |||
| + | Коэффициент детерминации j-ого признака относительно остальных вычисляется следующим образом: | ||
| + | |||
| + | <center><tex>R_j^2 = 1 - \frac{||\mathbf{x}_j - X_{A\setminus\{j\}\mathbf{w}}||^2}{||\mathbf{x}_j - 1 \overline{x_j}||^2},</tex></center> | ||
| + | |||
| + | где <tex>\overline{x_j}</tex> - среднее значение вектроа <tex>\mathbf{x}_j</tex> | ||
| + | |||
| + | |||
| + | |||
| + | Требуется найти такую модель оптимальной структуры признаков <tex>F</tex>, которая доставляет наименьшее значение функционалу качества (2). | ||
| + | |||
| + | == Порождение свободных переменных == | ||
| + | Множества измеряемых признаков бывает недостаточно для построения модели удовлетворительного качества. Требуется расширить множество признаков с помощью функциональных преобразований. | ||
| + | |||
| + | Предлагается следующий способ порождения новых признаков: | ||
| + | |||
| + | Пусть задано множество свободных переменных <tex>Z = \{\xi_u\}^U_{u=1}</tex> и конечное множество порождающих функций <tex>G = \{g_v\}^V_{v=1}</tex>. | ||
| + | |||
| + | Обозначим <tex>a_i = g_v(\xi_u)</tex>, где индекс <tex>i = (v - 1)U + u</tex>. | ||
| + | |||
| + | Рассмотрим декартово произведение <tex>Z \times G</tex>, где элементу <tex>(g_v,\xi_u)</tex> ставится в соответствие суперпозиция <tex>g_v(\xi_u)</tex>, однозначно определяемая индексами <tex>v,u</tex>. | ||
| + | |||
| + | В качестве модели, описывающей отношение между зависимой переменной <tex>y</tex> и свободными переменными <tex>a_i</tex>, используется полином Колмогорова-Габора: | ||
| + | |||
| + | |||
| + | <center><tex>y=w_0+\sum_{\alpha=1}^{UV}w_{\alpha}a_{\alpha} + \sum_{\alpha=1}^{UV}\sum_{\beta=1}^{UV}w_{{\alpha}{\beta}}a_{\alpha}a_{\beta} + \ldots +\sum_{\alpha=1}^{UV}\ldots\sum_{\psi=1}^{UV}w_{{\alpha} \ldots {\psi}}a_{\alpha}\ldots a_{\psi}</tex></center>, | ||
| + | |||
| + | |||
| + | где <tex>\mathbf{w} = (w_0, w_{\alpha}, w_{\alpha\beta}, \ldots , w_{{\alpha} \ldots {\psi}})^T</tex> и <tex>{\alpha, \beta, \ldots , \psi = 1 \ldots UV}</tex>. | ||
| + | |||
| + | |||
| + | <tex> \{0\} \cup \{\alpha\} \cup \{\alpha,\beta\} \cup \ldots \cup \{\alpha,\beta \ldots \psi\} \rightarrow \Omega </tex> - множество индексов, размерности N. | ||
| + | |||
| + | <center><tex>\xi_u~ \longrightarrow\longrightarrow\longrightarrow^{g_v}\longrightarrow\longrightarrow ~g_v(\xi_u) ~=^{def} a_i~\longrightarrow\longrightarrow^{\prod^{UV}_{\alpha=1}}\longrightarrow^{\ldots}\longrightarrow^{\prod^{UV}_{\psi=1}}\longrightarrow ~x_j</tex></center> | ||
== Алгоритм == | == Алгоритм == | ||
| + | Рассмотрим алгоритм, состоящий из двух шагов. | ||
| + | На первом шаге мы будем добавлять признаки один за другим к нашей модели согласно критерию качества модели (2). | ||
| + | |||
| + | На втором шаге мы будем удалять признаки по одному из нашей модели согласно тому же критерию качества (2). | ||
| + | |||
| + | Пусть на <tex>k</tex>-ом шагу алгоритма имеется множество признаков <tex>A</tex>, которое определяет матрицу <tex>X_A</tex>: <tex>\mathbf{y} = X_A \mathbf{w}</tex>. | ||
| + | |||
| + | На нулевом шаге <tex>A_0 = \emptyset</tex>. Опишем <tex>k</tex>-ый шаг алгоритма. | ||
| + | |||
| + | |||
| + | ===Шаг 1: добавление признаков=== | ||
| + | |||
| + | Добавляем такой признак <tex>j \in J \setminus A_{k-1}</tex> к активному набору | ||
| + | <tex>A_k = A_{k-1} \cup \{j\}</tex>, | ||
| + | который доставляет минимум функционалу (2). | ||
| + | |||
| + | |||
| + | <center><tex>j = \arg\min_{j\in J \setminus A_{k-1}} S(X_A_k, \mathbf{y})</tex></center> | ||
| + | |||
| + | |||
| + | Пусть <center><tex>k^* = \arg\max_{t=1,\ldots,k} Evidence_t</tex></center> | ||
| + | |||
| + | Если выполнено условие: | ||
| + | |||
| + | <center><tex>|Evidence_k - \max_{t\in\{1,...,k-1\}}(Evidence_{t})| \geq \triangle E</tex>,</center> | ||
| + | |||
| + | то идём к шагу 2, иначе - повторяем шаг 1. | ||
| + | |||
| + | d - заданная константа. | ||
| + | |||
| + | ===Шаг 2: удаление признаков=== | ||
| + | |||
| + | Удаляем такой признак <tex>j \in A_{k-1}</tex> из активного набора | ||
| + | <tex>A_k = A_{k-1} \setminus \{j\}</tex>, | ||
| + | который имеет наибольший фактора инфляции дисперсии, то есть доставляет максимум функционалу (3). | ||
| + | |||
| + | |||
| + | <center><tex>j = \arg\max_{j\in A_{k-1}} VIF_j</tex></center> | ||
| + | |||
| + | |||
| + | Пусть <center><tex>k^* = \arg\max_{t=1,\ldots,k} Evidence_t</tex></center> | ||
| + | |||
| + | Если выполнено условие: | ||
| + | |||
| + | <center><tex>|Evidence_k - \max_{t\in\{1,...,k-1\}}(Evidence_{t})| \geq \triangle E</tex>,</center> | ||
| + | |||
| + | то идём к шагу 1, иначе - повторяем шаг 2. | ||
| + | |||
| + | d - заданная константа. | ||
| + | |||
| + | ===Критерий останова=== | ||
| + | Алгоритм заканчивает работу, если правдоподобие <tex>Evidence_k</tex> перестаёт увеличиваться. | ||
| + | |||
| + | Тогда мы нашли оптимальный набор признаков. | ||
== Вычислительный эксперимент == | == Вычислительный эксперимент == | ||
| - | == | + | Генерирование случайных данных: |
| + | <source lang="matlab"> | ||
| + | |||
| + | m = 300; %число объектов | ||
| + | U = 6; %число начальных признаков | ||
| + | V = 4; %количестов порождающих функций | ||
| + | d = 1; %на сколько шагов можно уйти от максимума | ||
| + | |||
| + | C = rand(m,U) | ||
| + | w = rand(U,1) | ||
| + | e = 0.1 * randn(m,1) | ||
| + | y = C*w + e | ||
| + | |||
| + | </source> | ||
| + | |||
| + | Порождение новых признаков: | ||
| + | <source lang="matlab"> | ||
| + | |||
| + | G = [Z, Z.^2, tan(Z), exp(Z)]; %множество порождающих функиций m на V*U | ||
| + | X = [ones(m,1), G]; %множество признаков m на N | ||
| + | |||
| + | N = size(X,1) | ||
| + | for i = 1 : U*V | ||
| + | for j = 1 : U*V | ||
| + | if i >= j | ||
| + | X = [X, G(:,i).*G(:,j)]; | ||
| + | N = N + 1; | ||
| + | end | ||
| + | end | ||
| + | end | ||
| + | |||
| + | </source> | ||
| + | |||
| + | Вычисление номера признака, доставляющего минимум функционалу качества (2): | ||
| + | <source lang="matlab"> | ||
| + | |||
| + | for i = 1:numel(ind) | ||
| + | mask2 = mask; | ||
| + | mask2(ind(i),1) = 1; | ||
| + | |||
| + | X_mask2 = getXmask(X, mask2); | ||
| + | [w, sse_] = lsqlin(X_mask2,y,[],[]); | ||
| + | |||
| + | if i == 1 | ||
| + | sse_best = sse_; | ||
| + | elseif sse_< sse_best | ||
| + | sse_best = sse_; | ||
| + | index_best = ind(i); | ||
| + | end | ||
| + | end | ||
| + | |||
| + | </source> | ||
| + | |||
| + | Вычисление правдоподобия: | ||
| + | <source lang="matlab"> | ||
| + | |||
| + | X_ = getXmask( X, mask ); | ||
| + | xRegression=X_; | ||
| + | yRegression=y; | ||
| + | activeSet = 1:size(xRegression,2); % количество активных признаков | ||
| + | |||
| + | [weightM,alphaM,beta,weightH,alphaMH,betaH,gammaH] = ... | ||
| + | getLinParam(xRegression,yRegression,activeSet); | ||
| + | beta; | ||
| + | evid_ = abs(getEvid( xRegression,yRegression,weightM,alphaM,beta )); | ||
| + | |||
| + | </source> | ||
| + | |||
| + | |||
| + | '''На графике выведем зависимость правдоподобия(ocь Y) от шага алгоритма(ось X)''' | ||
| + | <source lang="matlab"> | ||
| + | evidence | ||
| + | plot(linspace(1,numel(evidence),numel(evidence)), evidence); | ||
| + | </source> | ||
| + | |||
| + | [[Изображение:evid_1.png|thumb|left]] | ||
| + | [[Изображение:evid_3.png|thumb|left]] | ||
| + | [[Изображение:evid_2.png|thumb|left]] | ||
| + | [[Изображение:evid_4.png|thumb|left]] | ||
| + | [[Изображение:evid_5.png|thumb|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Эксперимент 1. | ||
| + | |||
| + | Количество объектов = 300, | ||
| + | количество начальных признаков = 6, | ||
| + | количество признаков = 230 | ||
| + | |||
| + | Порождающие функции: <tex>g = \{x,~x^2,~\tan(x),~\exp(x)\}</tex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Эксперимент 2. | ||
| + | |||
| + | Количество объектов = 300, | ||
| + | количество начальных признаков = 6, | ||
| + | количество признаков = 230 | ||
| + | |||
| + | Порождающие функции: <tex>g = \{x,~x^2,~\tan(x),~\exp(x)\}</tex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Эксперимент 3. | ||
| + | |||
| + | Количество объектов = 500, | ||
| + | количество начальных признаков = 6, | ||
| + | количество признаков = 230 | ||
| + | |||
| + | Порождающие функции: <tex>g = \{x,~x^2,~\tan(x),~\exp(x)\}</tex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Эксперимент 4. | ||
| + | |||
| + | Количество объектов = 500, | ||
| + | количество начальных признаков = 6, | ||
| + | количество признаков = 230 | ||
| + | |||
| + | Порождающие функции: <tex>g = \{\frac{1}{x}, x,~x^2,~\tan(x),~\exp(x)\}</tex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Эксперимент 5. | ||
| + | |||
| + | Количество объектов = 900, | ||
| + | количество начальных признаков = 7, | ||
| + | количество признаков = 441 | ||
| + | |||
| + | Порождающие функции: <tex>g = \{\frac{1}{x}, x,~x^2,~\tan(x),~\exp(x)\}</tex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
== Литература == | == Литература == | ||
# {{книга | # {{книга | ||
| Строка 29: | Строка 307: | ||
|год = 2010 | |год = 2010 | ||
}} | }} | ||
| + | # {{книга | ||
| + | |автор = Стрижов В.В | ||
| + | |заглавие = Методы индуктивного порождения регрессионных моделей | ||
| + | |издательство = ВЦ РАН | ||
| + | |год = 2008 | ||
| + | }} | ||
| + | # {{книга | ||
| + | |автор = Vadim Strijov, Katya Krymova, Gerhard Wilhelm Weber | ||
| + | |заглавие = Evidence Optimization for Consequently Generated Models | ||
| + | |издательство = Computing Center of the Russian Academy of Science, Moscow, Russia | ||
| + | |год = 2010 | ||
| + | }} | ||
| + | |||
| + | == Исходный код == | ||
| + | [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/MIPT2006-2010OldProj/Minaev2010Maximum/ Minaev2010Maximum] | ||
| + | |||
| + | {{ЗаданиеВыполнено|Павел Минаев|В.В.Стрижов|24 декабря 2010||Strijov}} | ||
| + | [[Категория:Практика и вычислительные эксперименты]] | ||
Текущая версия
Содержание |
Постановка задачи
Пусть задана выборка из m пар.
- множество из m объектов,
, где n - количество признаков, а
- соответствующая зависимая переменная.
- вектор значений j-ого признака, а
- вектор целевого признака.
Пусть - множество индексов объектов,
- множество индексов признаков.
- подмножество активных признаков.
Множество
задаёт регрессионную модель
, а
- сложность модели.
Рассмотрим следующую линейную модель регрессии, описывающую связь между свободными и зависимой переменными
где - вектор параметров регрессии, а случайная аддитивная переменная
регрессионной модели имеет нормальное распределение
.
Распределение зависимой переменной будет иметь следующий вид:
где - сумма квадратов невязок
. Согласно оценки точки наибольшего правдоподобия, данное распределение задаёт критерий качества модели, равный сумме квадратов регрессионных остатков.
где - некоторое множество индексов. Этот критерий используется при выборе модели в дальнейшем.
Мультиколлинеарность отслеживается с помощью фактора инфляции дисперсии (VIF), связанного с корреляцей данного признака с другими:
Коэффициент детерминации j-ого признака относительно остальных вычисляется следующим образом:
где - среднее значение вектроа
Требуется найти такую модель оптимальной структуры признаков , которая доставляет наименьшее значение функционалу качества (2).
Порождение свободных переменных
Множества измеряемых признаков бывает недостаточно для построения модели удовлетворительного качества. Требуется расширить множество признаков с помощью функциональных преобразований.
Предлагается следующий способ порождения новых признаков:
Пусть задано множество свободных переменных и конечное множество порождающих функций
.
Обозначим , где индекс
.
Рассмотрим декартово произведение , где элементу
ставится в соответствие суперпозиция
, однозначно определяемая индексами
.
В качестве модели, описывающей отношение между зависимой переменной и свободными переменными
, используется полином Колмогорова-Габора:
где и
.
- множество индексов, размерности N.
Алгоритм
Рассмотрим алгоритм, состоящий из двух шагов.
На первом шаге мы будем добавлять признаки один за другим к нашей модели согласно критерию качества модели (2).
На втором шаге мы будем удалять признаки по одному из нашей модели согласно тому же критерию качества (2).
Пусть на -ом шагу алгоритма имеется множество признаков
, которое определяет матрицу
:
.
На нулевом шаге . Опишем
-ый шаг алгоритма.
Шаг 1: добавление признаков
Добавляем такой признак к активному набору
,
который доставляет минимум функционалу (2).
Если выполнено условие:
то идём к шагу 2, иначе - повторяем шаг 1.
d - заданная константа.
Шаг 2: удаление признаков
Удаляем такой признак из активного набора
,
который имеет наибольший фактора инфляции дисперсии, то есть доставляет максимум функционалу (3).
Если выполнено условие:
то идём к шагу 1, иначе - повторяем шаг 2.
d - заданная константа.
Критерий останова
Алгоритм заканчивает работу, если правдоподобие перестаёт увеличиваться.
Тогда мы нашли оптимальный набор признаков.
Вычислительный эксперимент
Генерирование случайных данных:
m = 300; %число объектов U = 6; %число начальных признаков V = 4; %количестов порождающих функций d = 1; %на сколько шагов можно уйти от максимума C = rand(m,U) w = rand(U,1) e = 0.1 * randn(m,1) y = C*w + e
Порождение новых признаков:
G = [Z, Z.^2, tan(Z), exp(Z)]; %множество порождающих функиций m на V*U X = [ones(m,1), G]; %множество признаков m на N N = size(X,1) for i = 1 : U*V for j = 1 : U*V if i >= j X = [X, G(:,i).*G(:,j)]; N = N + 1; end end end
Вычисление номера признака, доставляющего минимум функционалу качества (2):
for i = 1:numel(ind) mask2 = mask; mask2(ind(i),1) = 1; X_mask2 = getXmask(X, mask2); [w, sse_] = lsqlin(X_mask2,y,[],[]); if i == 1 sse_best = sse_; elseif sse_< sse_best sse_best = sse_; index_best = ind(i); end end
Вычисление правдоподобия:
X_ = getXmask( X, mask ); xRegression=X_; yRegression=y; activeSet = 1:size(xRegression,2); % количество активных признаков [weightM,alphaM,beta,weightH,alphaMH,betaH,gammaH] = ... getLinParam(xRegression,yRegression,activeSet); beta; evid_ = abs(getEvid( xRegression,yRegression,weightM,alphaM,beta ));
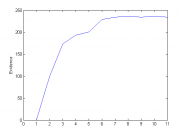
На графике выведем зависимость правдоподобия(ocь Y) от шага алгоритма(ось X)
evidence plot(linspace(1,numel(evidence),numel(evidence)), evidence);
Эксперимент 1.
Количество объектов = 300, количество начальных признаков = 6, количество признаков = 230
Порождающие функции:
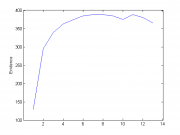
Эксперимент 2.
Количество объектов = 300, количество начальных признаков = 6, количество признаков = 230
Порождающие функции:
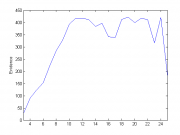
Эксперимент 3.
Количество объектов = 500, количество начальных признаков = 6, количество признаков = 230
Порождающие функции:
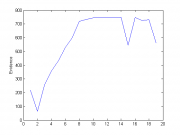
Эксперимент 4.
Количество объектов = 500, количество начальных признаков = 6, количество признаков = 230
Порождающие функции:
Эксперимент 5.
Количество объектов = 900, количество начальных признаков = 7, количество признаков = 441
Порождающие функции:
Литература
- Стрижов В.В Методы выбора регрессионных моделей. — ВЦ РАН, 2010.
- Стрижов В.В Методы индуктивного порождения регрессионных моделей. — ВЦ РАН, 2008.
- Vadim Strijov, Katya Krymova, Gerhard Wilhelm Weber Evidence Optimization for Consequently Generated Models. — Computing Center of the Russian Academy of Science, Moscow, Russia, 2010.
Исходный код
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |