SVM регрессия (пример)
Материал из MachineLearning.
м (→Литература) |
(→Исходный код) |
||
| (5 промежуточных версий не показаны.) | |||
| Строка 35: | Строка 35: | ||
<tex> | <tex> | ||
\begin{cases} | \begin{cases} | ||
| - | \frac{1}{2} (w,w) | + | \frac{1}{2} (w,w) + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\ |
(w,f(x_i))-w_0 \le y_i + \epsilon + \xi_i^+, & i=1,..,\ell; \\ | (w,f(x_i))-w_0 \le y_i + \epsilon + \xi_i^+, & i=1,..,\ell; \\ | ||
(w,f(x_i))-w_0 \ge y_i - \epsilon - \xi_i^-, & i=1,..,\ell; \\ | (w,f(x_i))-w_0 \ge y_i - \epsilon - \xi_i^-, & i=1,..,\ell; \\ | ||
| Строка 43: | Строка 43: | ||
</tex> | </tex> | ||
| - | Эту же задачу можно преобразовать к виду <tex>\frac{1}{2}u^T H u + g u\rightarrow \underset{u}{min}</tex>, при условии, что <tex>A u \le b,\ </tex>а также, <tex>lb \le u</tex>, где <tex>u</tex> - вектор-столбец, составленный из столбцов <tex>w\ , \xi_i^+, \xi_i^-</tex>, тоесть, где все переменные | + | Эту же задачу можно преобразовать к виду <tex>\frac{1}{2}u^T H u + g u\rightarrow \underset{u}{min}</tex>, при условии, что <tex>A u \le b,\ </tex>а также, <tex>lb \le u</tex>, где <tex>u</tex> - вектор-столбец, составленный из столбцов <tex>w\ , \xi_i^+, \xi_i^-</tex>, тоесть, где все переменные объединены в один столбец неизвестных. В таких обозначениях <tex>H=diag(1,1,...,1,0,0,...,0),\ g=(0,0,...,0,1,1,...,1)</tex>, где единиц и нулей в <tex>H</tex> и <tex>g</tex> соответственно столько же, сколько порождающих функций, а размерность матрицы <tex>H</tex> и вектора <tex>g</tex> равна размерности <tex>u</tex>. |
Теперь построим матрицу А и столбцы <tex>b</tex> и <tex>lb</tex>. Преобразуем задачу квадратичного программирования к виду | Теперь построим матрицу А и столбцы <tex>b</tex> и <tex>lb</tex>. Преобразуем задачу квадратичного программирования к виду | ||
| Строка 49: | Строка 49: | ||
<tex> | <tex> | ||
\begin{cases} | \begin{cases} | ||
| - | \frac{1}{2} (w,w) | + | \frac{1}{2} (w,w) + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\ |
(w,f(x_i)) - w_0 -\xi_i^+ \le y_i + \epsilon , & i=1,..,\ell; \\ | (w,f(x_i)) - w_0 -\xi_i^+ \le y_i + \epsilon , & i=1,..,\ell; \\ | ||
-(w,f(x_i))+ w_0 -\xi_i^- \le -y_i + \epsilon , & i=1,..,\ell; \\ | -(w,f(x_i))+ w_0 -\xi_i^- \le -y_i + \epsilon , & i=1,..,\ell; \\ | ||
| Строка 94: | Строка 94: | ||
== Вычислительный эксперимент == | == Вычислительный эксперимент == | ||
| - | Вычислительный | + | Вычислительный эксперимент состоит из трех основных частей: |
* Генерация данных; | * Генерация данных; | ||
* Работа алгоритма; | * Работа алгоритма; | ||
| Строка 101: | Строка 101: | ||
=== Генерация данных === | === Генерация данных === | ||
| - | При генерации данных мы выбираем некую линейную комбинацию наших порождающих функций, и | + | При генерации данных мы выбираем некую линейную комбинацию наших порождающих функций, и добавляем к ней случайный шум. В ходе эксперимента исследуются различные, как дискретные, так и непрерывные шумы. В качестве базовой функции выбрана функция <tex>y = 3 + x - 1.5sin(x)</tex>. А в качестве порождающих функций <tex>x,\ e^x,\ sin(x),\ cos(x),\ x^{\frac{1}{2}},\ x^{\frac{3}{2}}, x^0</tex>. |
=== Нормальное распределение === | === Нормальное распределение === | ||
| Строка 129: | Строка 129: | ||
[[Изображение:Svr Poisson3.png|800px]] | [[Изображение:Svr Poisson3.png|800px]] | ||
| - | <tex>\Uparrow</tex>Часть предыдущего графика, на которой мы видим, что даже с идеальными данными мы не получим идеальное приближение, т.к. среди прочего минимизируем <tex>(w,w)</tex> | + | <tex>\Uparrow</tex>Часть предыдущего графика, на которой мы видим, что даже с идеальными данными мы не получим идеальное приближение, т.к. среди прочего минимизируем <tex>(w,w)</tex>. Функционал потерь состоит из суммы двух частей: <tex>\frac{1}{2} (w,w)</tex> и <tex>C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)</tex>. Если точки идут довольно ровно (дисперсия мала по сравнению с <tex>\epsilon</tex>), то можно выделить целое семейство функций, которые обращают вторую часть в ноль, но при этом первая часть будет принимать различные значения для различных наборов коэффициентов <tex>w</tex>. Таким образом, мы в качестве решения получим функцию из семества с минимальным <tex>\frac{1}{2} (w,w)</tex>, и она будет отличаться от точного решения. |
[[Изображение:Weights poisson.png|800px]] | [[Изображение:Weights poisson.png|800px]] | ||
| Строка 146: | Строка 146: | ||
=== Распределение sin(unif) === | === Распределение sin(unif) === | ||
| - | Тест на распределении вида sin(unifrnd(-3.1415/2,3.1415/2)) | + | Тест на распределении вида <tex>\frac{sin(unifrnd(-3.1415/2,3.1415/2))}{parameter}</tex>, или же синуса от равномерного распределения. |
[[Изображение:Svr Sin.png|800px]] | [[Изображение:Svr Sin.png|800px]] | ||
| Строка 161: | Строка 161: | ||
=== Реальные данные === | === Реальные данные === | ||
| - | Пример взят из [http://archive.ics.uci.edu/ml/datasets/Auto+MPG Репозитория UCI]. В этом примере рассматриваются автомобили 1970-1973 года выпуска. Строится зависимость | + | Пример взят из [http://archive.ics.uci.edu/ml/datasets/Auto+MPG Репозитория UCI]. В этом примере рассматриваются автомобили 1970-1973 года выпуска. Строится зависимость мощности автомобиля [л.с.] от веса [кг] |
[[Изображение:Svr UCI Auto mpg1.png|800px]] | [[Изображение:Svr UCI Auto mpg1.png|800px]] | ||
| Строка 167: | Строка 167: | ||
<tex>\Uparrow</tex>Пример иллюстрирует, что очень важно правильно выбирать порождающие функции. Хотя потери меньше, чем на следующем графике, такое решение не является достаточно точным. | <tex>\Uparrow</tex>Пример иллюстрирует, что очень важно правильно выбирать порождающие функции. Хотя потери меньше, чем на следующем графике, такое решение не является достаточно точным. | ||
| - | <tex>\Uparrow</tex>Вектор порождающих функций: f = [x, | + | <tex>\Uparrow</tex>Вектор порождающих функций: <tex>f = [x,\ e^{-x},\ sin(x),\ cos(x),\ x^{\frac{1}{2}},\ x^{\frac{3}{2}},\ x^0]</tex>; |
[[Изображение:Svr UCI Auto mpg2.png|800px]] | [[Изображение:Svr UCI Auto mpg2.png|800px]] | ||
| - | <tex>\Uparrow</tex>Вектор порождающих функций: f = [x, | + | <tex>\Uparrow</tex>Вектор порождающих функций: <tex>f = [x,\ e^{-x},\ x^2,\ 0*cos(x),\ x^{\frac{1}{2}},\ x^{\frac{3}{2}},\ x^0]</tex>; |
== Исходный код == | == Исходный код == | ||
| - | * Исходный код [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/ | + | * Исходный код [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group774/Kornienko2010SVMRegression Matlab] |
== Смотри также == | == Смотри также == | ||
| Строка 185: | Строка 185: | ||
* Gunn, S., 1998. Support Vector Machines for Classification and Regression. ISIS Technical Report ISIS-1-98. Image Speech & Intelligent Systems Research Group, University of Southampton, U.K. | * Gunn, S., 1998. Support Vector Machines for Classification and Regression. ISIS Technical Report ISIS-1-98. Image Speech & Intelligent Systems Research Group, University of Southampton, U.K. | ||
| - | {{ЗаданиеВыполнено|Алексей Корниенко|В.В.Стрижов|28 мая 2010}} | + | {{ЗаданиеВыполнено|Алексей Корниенко|В.В.Стрижов|28 мая 2010|Korial|Strijov}} |
| - | [[Категория: | + | [[Категория:Практика и вычислительные эксперименты]] |
[[Категория:Классификация]] | [[Категория:Классификация]] | ||
[[Категория:Линейные классификаторы]] | [[Категория:Линейные классификаторы]] | ||
Текущая версия
SVM (Support Vector Machine, машина опорных векторов) — это особый класс алгоритмов, который характеризуется использованием ядер, отсутствием локальных минимумов, и используется для решения задач классификации и регрессии. В этой статье рассматривается пример использования метода опорных векторов в задачах регрессии.
Содержание |
Постановка задачи
Дано: Обучающая выборка , где
-признаковое описание i-го объекта,
- характеристика, приписываемая объекту. Функция потерь имеет вид
для каждого вектора
, где
.
Найти: такую функцию , которая описывает зависимость
наилучшим образом.
Алгоритм
В этом примере решается задача построения линейной SVM регрессии. Для этого решается прямая задача минимизации функционала потерь, в предположении что решение задается линейной комбинацией неких порождающих функций, из которых можем составить вектор-функцию
.
Тогда функционал примет вид:
В предположении что
Для этого вводятся обозначение и дополнительные переменные
и
:
,
,
.
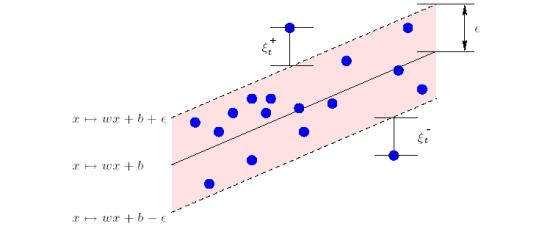
Геометрический смысл и
:
Далее решается задача квадратичного программирования:
Эту же задачу можно преобразовать к виду , при условии, что
а также,
, где
- вектор-столбец, составленный из столбцов
, тоесть, где все переменные объединены в один столбец неизвестных. В таких обозначениях
, где единиц и нулей в
и
соответственно столько же, сколько порождающих функций, а размерность матрицы
и вектора
равна размерности
.
Теперь построим матрицу А и столбцы и
. Преобразуем задачу квадратичного программирования к виду
Получаем,
, и количество минус бесконечностей в lb равно количеству порождающих функций, а количество нулей равно
.
Таким образом, мы свели задачу к задаче квадратичного программирования.
В нашем примере значения С, и порождающие функции задаются экспертом.
Вычислительный эксперимент
Вычислительный эксперимент состоит из трех основных частей:
- Генерация данных;
- Работа алгоритма;
- Визуализация и анализ данных.
Генерация данных
При генерации данных мы выбираем некую линейную комбинацию наших порождающих функций, и добавляем к ней случайный шум. В ходе эксперимента исследуются различные, как дискретные, так и непрерывные шумы. В качестве базовой функции выбрана функция . А в качестве порождающих функций
.
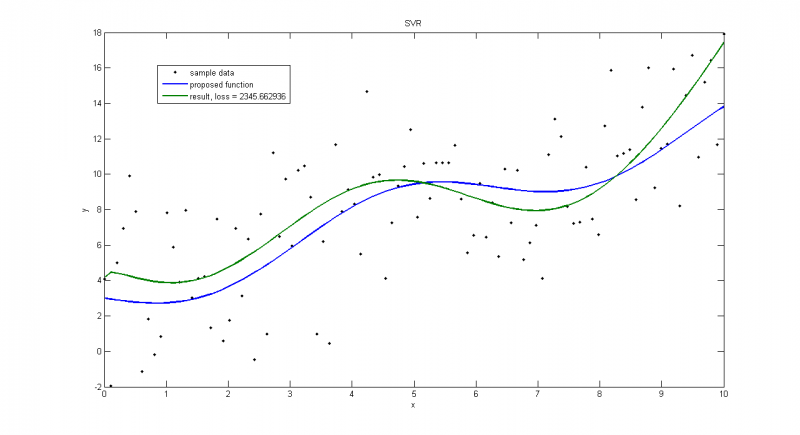
Нормальное распределение
дисперсия=1
дисперсия=0.1
Зависимость весов соответствующих функций от обратной дисперсии
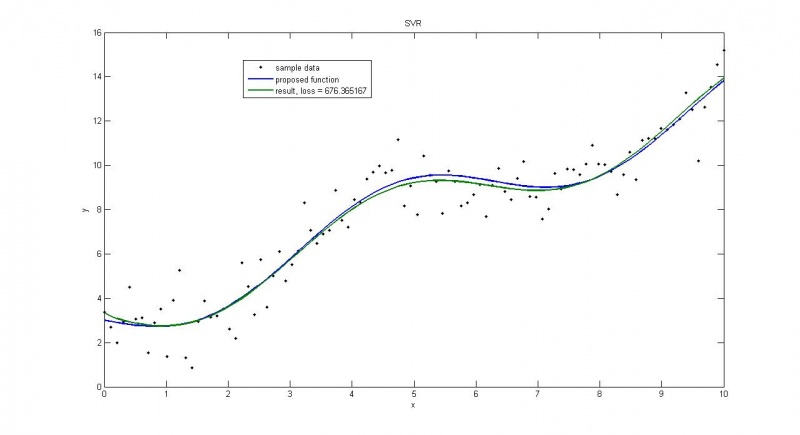
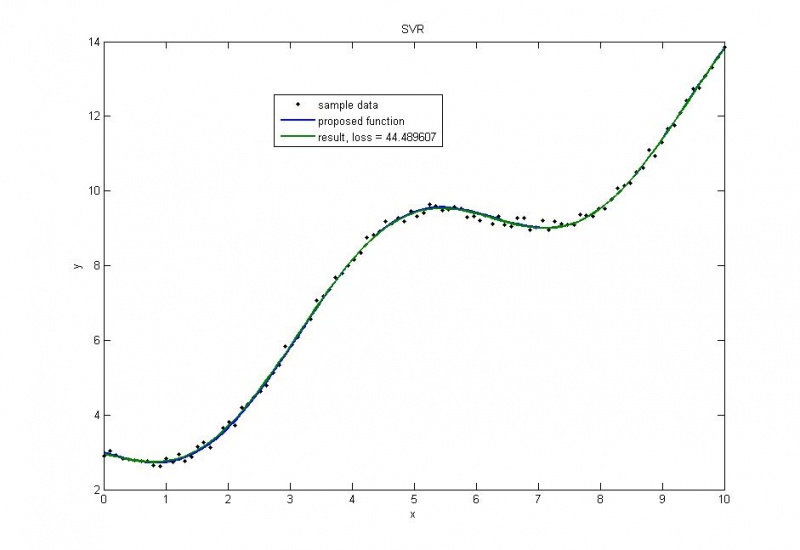
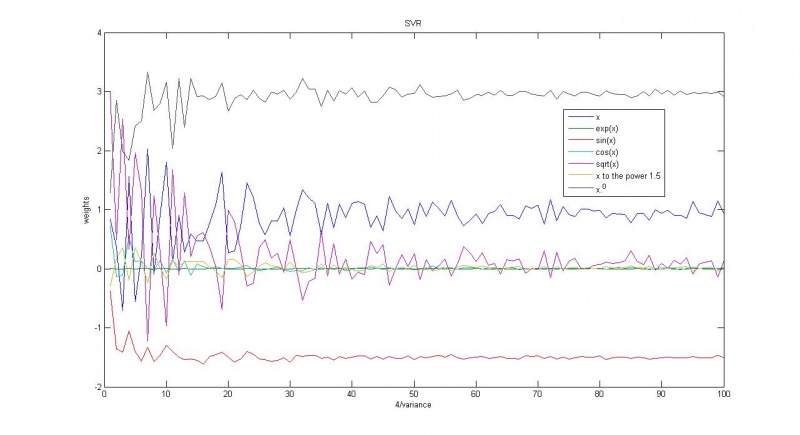
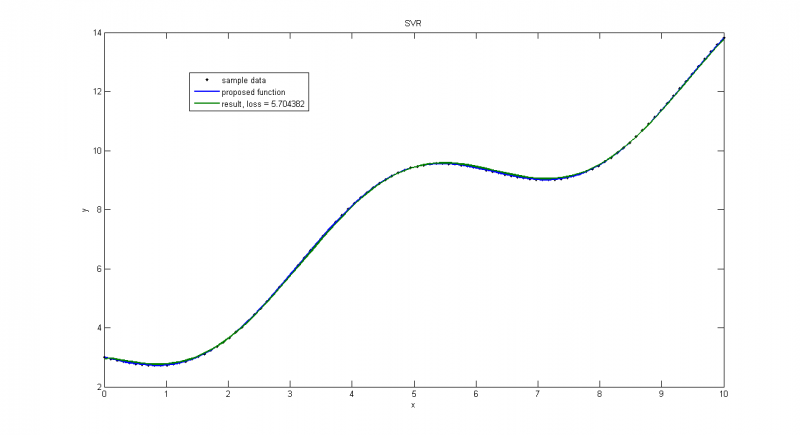
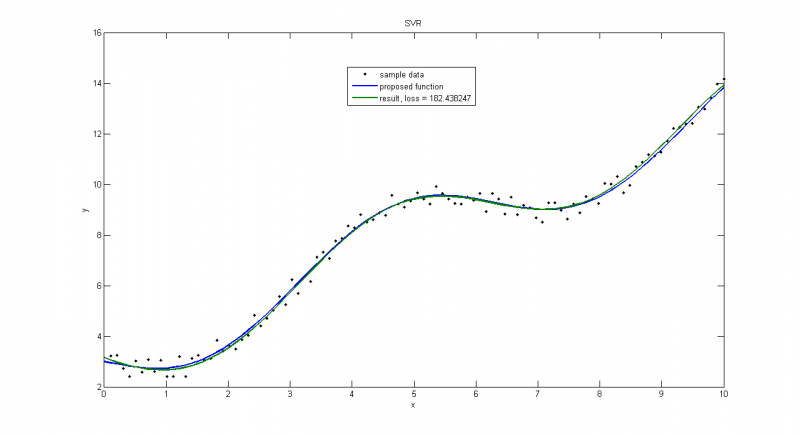
Пуассоновское распределение
Пуассоновское распределение с большой дисперсией
Пуассоновское распределение с малой дисперсией, получаем почти точное решение
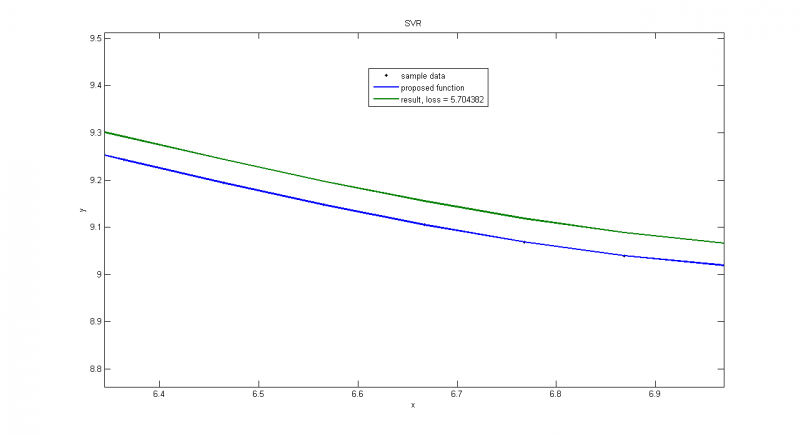
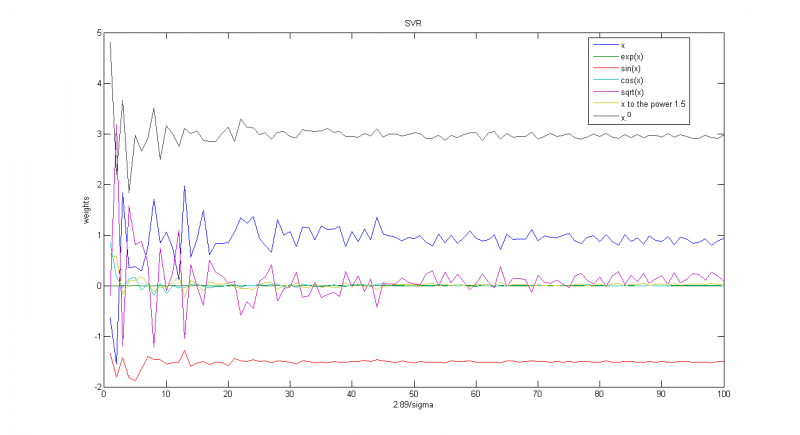
Часть предыдущего графика, на которой мы видим, что даже с идеальными данными мы не получим идеальное приближение, т.к. среди прочего минимизируем
. Функционал потерь состоит из суммы двух частей:
и
. Если точки идут довольно ровно (дисперсия мала по сравнению с
), то можно выделить целое семейство функций, которые обращают вторую часть в ноль, но при этом первая часть будет принимать различные значения для различных наборов коэффициентов
. Таким образом, мы в качестве решения получим функцию из семества с минимальным
, и она будет отличаться от точного решения.
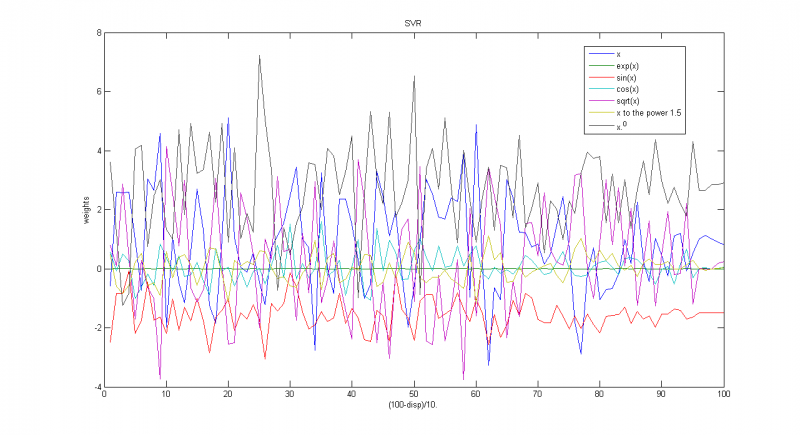
Зависимость весов соответствующих функций от параметра
Равномерное распределение
Работа алгоритма на примере с равномерным шумом. На этом графике шум равномерно распределен на отрезке
Зависимость весов соответствующих функций от параметра
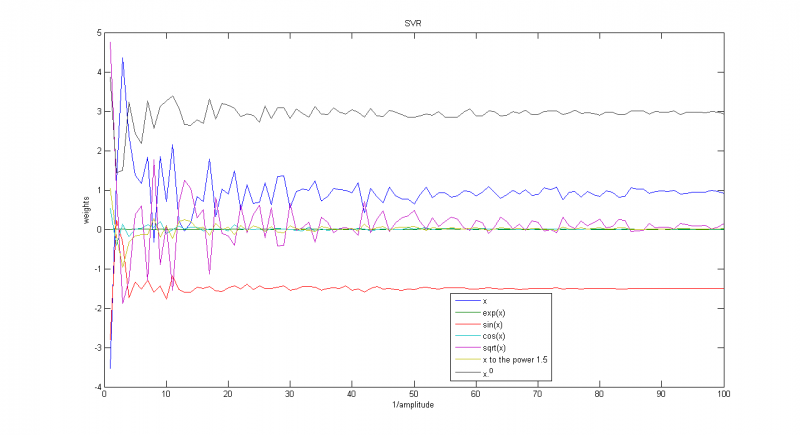
Распределение sin(unif)
Тест на распределении вида , или же синуса от равномерного распределения.
Если выбрать большую амплитуду(=5), решение может сильно отличаться от верного
При малых(=0.5) такого не наблюдается.
Зависимость весов соответствующих функций от параметра
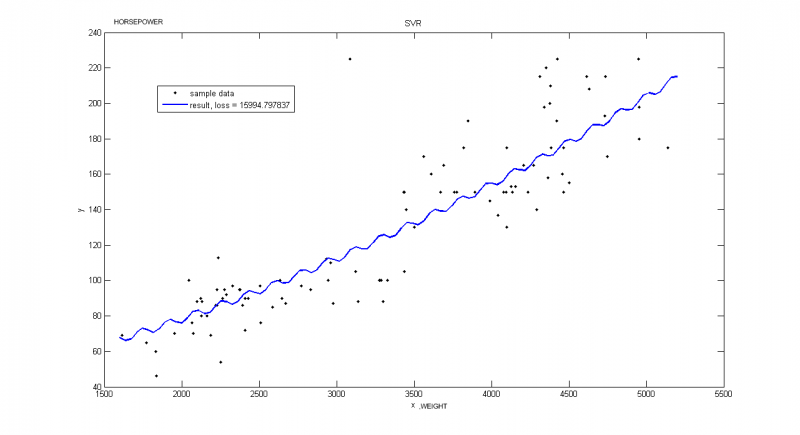
Реальные данные
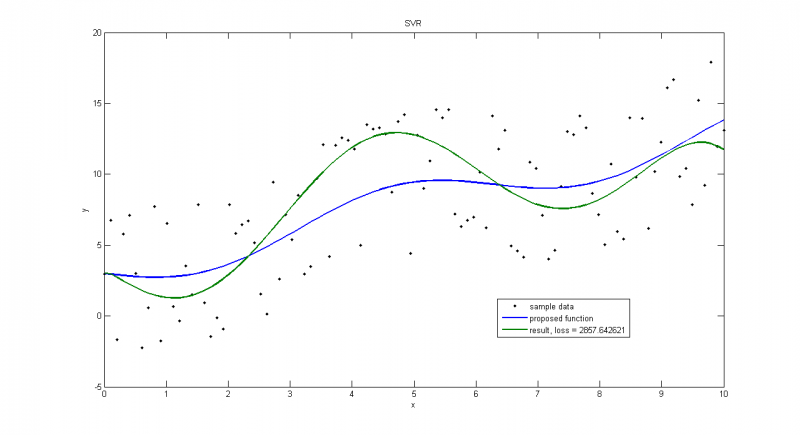
Пример взят из Репозитория UCI. В этом примере рассматриваются автомобили 1970-1973 года выпуска. Строится зависимость мощности автомобиля [л.с.] от веса [кг]
Пример иллюстрирует, что очень важно правильно выбирать порождающие функции. Хотя потери меньше, чем на следующем графике, такое решение не является достаточно точным.
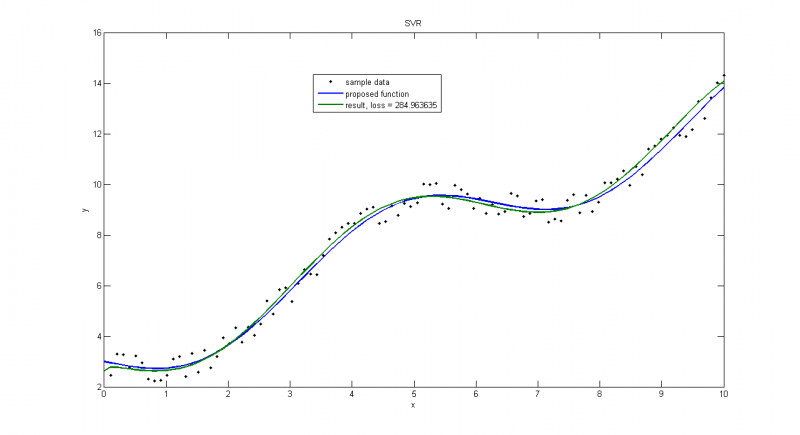
Вектор порождающих функций:
;
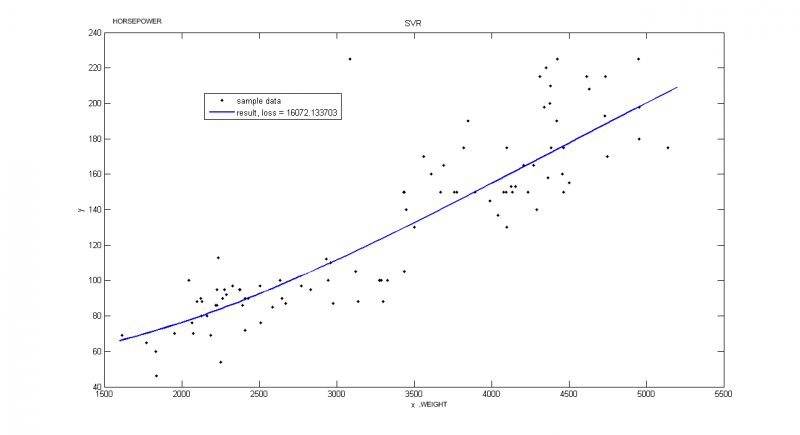
Вектор порождающих функций:
;
Исходный код
- Исходный код Matlab
Смотри также
Литература
- Alex J. Smola, Bernhard Schölkopf. A tutorial on support vector regression. DOI Bookmark: 10.1023/B:STCO.0000035301.49549.88
- Gunn, S., 1998. Support Vector Machines for Classification and Regression. ISIS Technical Report ISIS-1-98. Image Speech & Intelligent Systems Research Group, University of Southampton, U.K.
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |