Прогнозирование объемов продаж групп товаров (отчет)

Материал из MachineLearning.

(Различия между версиями)

Перейти к: навигация, поиск

Текущая версия

Введение в проект

Описание проекта

Цель проекта

Цель проекта — прогнозирование еженедельных покупок товаров. Горизонт прогнозирования — одна неделя.

Обоснование проекта

Полученные результаты могут быть использованы для планирования закупок товаров магазинами.

Описание данных

Дан региональный классификатор магазинов, товарный классификатор, ряды продаж по SKU (stock keeping unit), информация о дефиците товара, список праздничных дней, разметка промо-акций для каждого товара и розничные цены на товары.

Критерии качества

Используется скользящий контроль — прогноз закупок товаров, сделанный исходя из данных на некотором начальном временном интервале, сравнивается с реальными продажами. Критерием качества служит сумма модулей отклонений прогноза от реальной величины закупок либо сумма квадратов отклонений.

Требования к проекту

Сумма модулей (либо квадратов) отклонений для разработанного алгоритма должен быть меньше, чем для базового алгоритма — скользящего среднего за предыдущий месяц.

Выполнимость проекта

Прогнозирование покупок товаров в празничные дни и во время промо-акций является отдельной задачей и в данном проекте не рассматривается.

Используемые методы

Предполагается, что товары могут быть агрегированы в группы, исходя из их цены и «близости» по товарному классификатору. Затем может быть осуществлен прогноз для получившихся групп товаров и «разбрасывание» результатов прогнозирования по отдельным товарам из групп.

Постановка задачи

Заданы временные ряды продаж товаров $x_{ij}(t) \in R$ — продажи $i$ -ого товара в $j$ -ом магазине за день $t$ ( $i \in I$ , $I$ — множество товаров; $j \in J$ , $J$ — множество магазинов; $t \in N$ — натуральное число), причем значения продаж известны при $t_0 \leq t \leq t_1$ . Также задан товарный классификатор, исходя из которого товары разбиваются на группы, образующие иерархическую стуктуру (например, какой-то товар может входить в группу «ЖК-телевизоры 15"», которая входит в «ЖК-телевизоры 10" - 17"» и далее в «ЖК-телевизоры», «Телевизоры» и «Бытовую технику»). Требуется для всех товаров и всех магазинов спрогнозировать продажи за неделю, следующую после $t_1$ , то есть значение величины

$y_{ij} = \sum_{t=t_1+1}^{t_1+7}x_{ij}(t).$

Для оценки качества прогнозов будем использовать скользящий контроль, помещая в обучающую выборку значения $x_{ij}(t)$ при $t \in [t_0, t_{max}]$ , $t_{max} < t_1$ . Как функционал качества будем использовать

$Q_{m}(Y, \hat{Y}) = \sum_{i, j}|y_{ij}-\hat{y}_{ij}|$

или

$Q_{s}(Y, \hat{Y}) = \sum_{i, j}(y_{ij}-\hat{y}_{ij})^2.$

Описание алгоритмов

Обзор литературы

Для прогноза спроса товаров в настоящее время используются различные: авторегрессия (autoregression, или AR), алгоритмы, основанные на модели скользящего среднего (moving average model, MA), их комбинации (ARMA и ARIMA) ([1], [2]), нейронные сети ([3], [4]). Однако в данной задаче количество временных рядов очень велико, что ограничивает возможные алгоритмы наиболее простыми, такими как скользящее среднее.

Базовые предположения

Будем предполагать, что вероятности продажи товаров из одной группы нижнего уровня (т.е. группы, в которую входят только товары, а не другие группы) во всех магазинах имеют одинаковое распределение. Таким образом, оценив это распределение, а также суммарные продажи всех товаров из группы нижнего уровня в некотором магазине (например, с помощью скользящего среднего), можно будет спрогнозировать продажи отдельных товаров точнее, чем используя базовый алгоритм (скользящее среднее по каждому товару). Также предполагается, что прогноз можно делать по отдельности для каждого из магазинов.

Математическое описание

Базовый алгоритм

Выбранный базовый алгоритм — скользящее среднее по каждому товару за предыдущий месяц:

$\hat{y}_{ij}^0 = \frac{7}{w} s_{ij}(w),$

где $w=30$ — ширина окна,

$s_{ij}(w)=\sum_{t = t_1-w+1}^{t_1}x_{ij}(t).$

Алгоритм группового учета

1. Найти все группы нижнего уровня — разбиение множества $I$ на непересекающиеся подмножества $I_k \subset I$ .

2. Для всех групп нижнего уровня $I_k$ повторять шаги 3-4:

3. Найти суммарные продажи товаров из $I_k$ во всех магазинах:

$S_{w} = \sum_{i \in I_k}\sum_{j \in J}s_{ij}(w)$ .

4. Определить доли продаж отдельных товаров из группы:

$D_w(i) =\frac{1}{S_w} \sum_{j \in J}s_{ij}(w)$ .

5. Повторять для всех $j \in J$ и всех групп нижнего уровня $I_k$ шаги 6-7:

6. Вычислить по методу скользящего среднего прогноз продаж товаров из $I_k$ в магазине $j$ на следующую неделю:

$S_{vj}(I_k) = \frac{7}{v} \sum_{i \in I_k}s_{ij}(v).$

7. Распределить предсказанное число товаров согласно величинам $D_w(i)$ :

$\hat{y}_{ij} = S_{vj}(I_k) D_w(i).$

Варианты или модификации

Ширина окна при усреднении

Вышеприведенный алгоритм использует усреднение два раза — при вычислении $D_w(i)$ и $S_{vj}(I_k)$ . Длина окна, которая при этом используется, не обязана совпадать — в общем случае $v \neq w$ . Этому можно дать простое объяснение: покупатели могут изменять предпочтения в пределах группы товаров медленнее или, наоборот, быстрее, чем меняется суммарный спрос на товары из группы. Обе длины $v$ и $w$ лучше всего определить с помощью скользящего контроля.

Дискретное количество товаров

В случае, если $x_{ij}(t)$ целые (и такими должны быть прогнозы $\hat{y}_{ij}$ ), алгоритм требует модификации. Существует несколько способов добиться целых значений $\hat{y}_{ij}$ :

Округлять полученные на последнем шаге алгоритма прогнозы.
Случайно распределять $[S_{vj}(I_k)]$ товаров в соответствии с вероятностями $D_w(i)$ .
Алгоритм RndDistribute (частичная рандомизация):

1. Из $[S_{vj}(I_k)]$ товаров определенную часть распределить детерминированно по формуле

$\hat{y}_{ij}^{fix} = \lfloor \alpha [S_{vj}(I_k)] D_w(i) \rfloor,$

где $0 \leq \alpha \leq 1$ .

2. Подсчитать оставшееся количество товаров:

$S^{\prime}(I_k) = [S_{vj}(I_k)] - \sum_{i \in I_k} \hat{y}_{ij}^{fix}.$

3. Пересчитать распределение товаров:

$D^{\prime}(i) = \frac{[S_{vj}(I_k)] D_w(i) - \hat{y}_{ij}^{fix}}{S^{\prime}(I_k)}.$

4. Распределить оставшиеся товары случайно согласно вероятностям $D^{\prime}(i)$ .

В частности, при $\alpha = 0$ этот метод совпадает с предыдущим.

Алгоритм MaxDistribute (полностью детерминированный вариант предыдущего метода):

1. Распределить максимально возможное количество товаров согласно вероятностям $D_w(i)$

$\hat{y}_{ij}^{fix} = \lfloor [S_{vj}(I_k)] D_w(i) \rfloor.$

2. Подсчитать оставшееся количество товаров:

$S^{\prime}(I_k) = [S_{vj}(I_k)] - \sum_{i \in I_k} \hat{y}_{ij}^{fix}.$

3. Пересчитать распределение товаров:

$D^{\prime}(i) = \frac{[S_{vj}(I_k)] D_w(i) - \hat{y}_{ij}^{fix}}{S^{\prime}(I_k)}.$

4. Оставшиеся товары распределить по одному среди типов товаров с максимальными вероятностями $D^{\prime}(i)$ .

Заметим, что алгоритм корректен, так как в любом случае $S^{\prime}(I_k) \leq |I_k|$ .

Оценки качества

Как отмечено ранее, для оценки качества предлагается использовать сумму модулей или квадратов отклонений прогноза от дейсвительных продаж. Однако эти функционалы качества отдают предпочтение прогнозам с меньшими количествами продаж, так как верхняя грань обоих функционалов зависит от суммарных прогнозируемых продаж:

$Q_{m}(Y, \hat{Y}) = \sum_{i,j}|y_{ij}-\hat{y}_{ij}| \leq Q_m^{max} = \sum_{i, j}y_{ij} + \sum_{i, j}\hat{y}_{ij},$

$Q_{s}(Y, \hat{Y}) = \sum_{i,j}(y_{ij}-\hat{y}_{ij})^2 \leq Q_{s}^{max} =\sum_{i, j}y_{ij}^2 + \sum_{i, j}\hat{y}_{ij}^2.$

Таким образом, лучше в качестве функционалов использовать соотношения:

$Q_{rm}(Y, \hat{Y}) = \frac{|y_{ij}-\hat{y}_{ij}|}{\sum_{i, j}y_{ij} + \sum_{i, j}\hat{y}_{ij}},$

$Q_{rs}(Y, \hat{Y}) = \frac{(y_{ij}-\hat{y}_{ij})^2}{\sum_{i, j}y_{ij}^2 + \sum_{i, j}\hat{y}_{ij}^2}.$

Разумеется, даже при таком подходе совершенно не учитывается взаимозаменяемость родственных товаров и т.п., что выходит за рамки сформулированной задачи.

Кластеризация магазинов

Исходный алгоритм был сформулирован в предположении, что распределение товаров одинаково во всех магазинах. В более общем случае магазины разбиваются на кластеры, исходя из выборочных значений распределения товаров. Модифицированный таким образом алгоритм будет иметь следующий вид:

1. Найти все группы нижнего уровня --- разбиение множества $I$ на непересекающиеся подмножества $I_k \subset I$ .

2. Для каждого магазина $j$ вычислить распределение товаров $D_{uj}(i)$ :

$\forall {i \in I_k}\ D_{uj}(i) = \frac{s_{ij}(u)}{\sum_{i \in I_k} s_{ij}(u)}.$

Используемая длина окна $u$ в общем случае отличается от $v$ и $w$ — большие значения $u$ обеспечивают большую статистическую надежность (особенно при небольшом спросе на товары). С другой стороны, при слишком больших длинах не учитывается изменение распределения с временем. Оптимальное $u$ находится с помощью скользящего контроля.

3. Вычислить расстояние между всеми парами распределений $D_{uj}$ и $D_{ul}$ . В качестве метрики можно использовать метрику $L_2$

$\rho (D_{uj}, D_{ul})=\sum_i (D_{uj}(i)-D_{ul}(i))^2,$

либо $L_1$

$\rho (D_{uj}, D_{ul})=\sum_i |D_{uj}(i)-D_{ul}(i)|.$

4. Исходя из расстояний, разбить магазины на $K$ кластеров. Оптимальное $K$ также находится с помощью скользящего контроля. Заметим, что при $K=1$ алгоритм превращается в алгоритм группового учета, а при $K=|J|$ — в базовый алгоритм.

5. Для каждого из кластеров применить шаги 2-7 алгоритма группового учета.

Теоретически, кластеризация магазинов может помочь при прогнозировании продаж товаров во время промо-акций, разделяя магазины, в которых проводятся или не проводятся промо-акции, в разные кластеры. Практически, возможности кластеризации ограничены из-за так называемого «проклятия размерности» (curse of dimensions).

Работа с промо-акциями

Продажи товаров во время промо-акций можно либо интерпретировать, как и продажи остальных товаров, либо игнорировать, принимая равными нулю.

Описание системы

Описание системы: [1].
Файлы системы находятся в папке [2].

Отчет о вычислительных экспериментах

Сравнение алгоритма с базовым

Сравнивались предсказания базового алгоритма и алгоритма группового учета с параметрами $K=1$ (т.е. кластеризация магазинов не проводилась), $w=10$ , $v=35$ . Для получения целочисленных предсказаний использовались: в случае базового алгоритма — простое округление, в случае алгоритма группового учета — алгоритм MaxDistribute, описанный ранее. Оценка качества проводилась с помощью скользящего контроля, при котором верхняя граница обучающей выборки $t_{max}$ последовательно принимала 120 разных значений с интервалом в 5 дней. Использовались функционалы качества $Q_{rm}$ и $Q_{rs}$ . 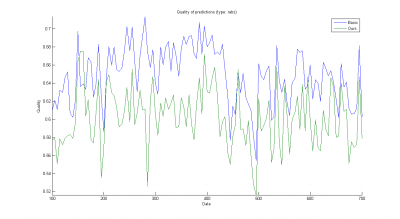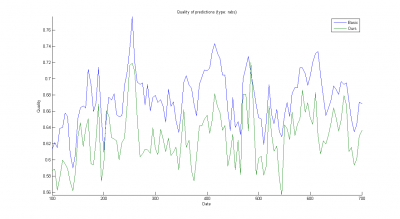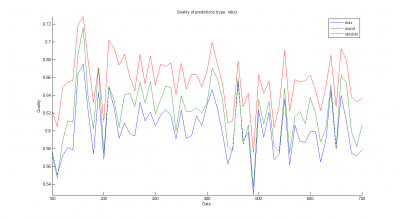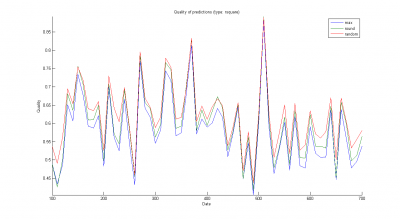Результаты работы приведены на рисунках ниже (зависимости качества от $t_{max}$ ; базовый алгоритм обозначен синим цветом, наш алгоритм — зеленым) и таблице.

Функционал	Алгоритм	Промо-акции оставлены	Промо-акции обнулены
$Q_{rm}$	базовый	64.9%	67.5%
$Q_{rm}$	групповой	60.2%	62.7%
$Q_{rs}$	базовый	62.2%	61.0%
$Q_{rs}$	групповой	58.1%	57.3%

Видно, что независимо от функционала качества и способа учета промо-акций алгоритм группового учета более эффетивен, чем базовый алгоритм. Тем не менее, значения функционалов качества все равно довольно велики и для нашего алгоритма. Это связано с тем, что продажи даже самых покупаемых товаров в отдельных магазинах малы и испытывают большие флуктуации.

Зависимость работы алгоритма от параметров

Зависимость от способа округления

Выше были приведены три способа получения целочисленных прогнозов: простое округление, рандомизация и алгоритм MaxDistribute. Для выбора предпочтительного метода использовался скользящий контроль, при котором верхняя граница обучающей выборки $t_{max}$ последовательно принимала 60 значений с интервалом в 10 дней; затем значения функционалов качества усреднялись.

Функционал	Метод	Промо-акции оставлены	Промо-акции обнулены
$Q_{rm}$	округление	62.1%	65.0%
$Q_{rm}$	рандомизация	65.6%	68.7%
$Q_{rm}$	MaxDistribute	60.2%	62.7%
$Q_{rs}$	округление	60.0%	59.7%
$Q_{rs}$	рандомизация	62.1%	62.9%
$Q_{rs}$	MaxDistribute	58.1%	57.1%

Во всех случаях лучшим оказался метод MaxDistribute, далее следует простое округление, а хуже всех — рандомизация.

Зависимость от $v$ и $w$

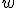
Для оценки качества при разных значениях параметров $v$ и $w$ использовался скользящий контроль, как и в предыдущем пункте. $w$ менялось от 3 до 30 дней с шагом в 3 дня, при этом полагалось $K = 1$ , $v = 35$ . $v$ менялось от 3 до 60 дней с шагом в 3 дня, полагалось $K = 1$ , $w = 10$ . Продажи во время промо-акций не занулялись (при занулении результаты аналогичны).

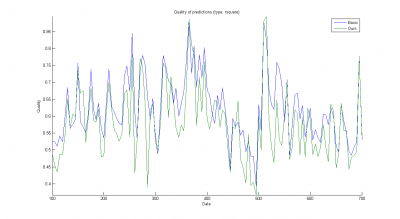
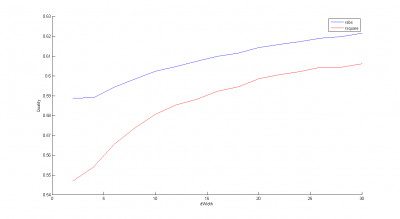
Результаты работы приведены ниже (синим обозначен функционал качества $Q_{rm}$ , красным — $Q_{rs}$ ). Видно, что качество прогнозов сильно зависит от $w$ , причем оптимальными являются минимальные значения (хотя это сложно обосновать теоретически). От $v$ качество зависит менее выраженно; оптимальными можно считать значения $v \geq 30$ .

Зависимость от количества кластеров 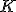$K$

При варьировании $K$ верхняя граница обучающей выборки $t_{max}$ последовательно принимала 13 значений с интервалом в 50 дней. Полагалось $w = 10$ , $v = 35$ , $u = 45$ ; для кластеризации использовалась метрика $L_1$ . Результаты приведены в таблице.

Промо-акции	Функционал	$K=1$	$K=2$	$K=3$	$K=4$	$K=5$
оставлены	$Q_{rm}$	60.48%	60.44%	60.61%	60.43%	60.84%
оставлены	$Q_{rs}$	56.19%	56.01%	56.17%	55.83%	56.25%
обнулены	$Q_{rm}$	63.33%	63.32%	63.25%	63.49%	63.51%
обнулены	$Q_{rs}$	57.30%	57.13%	57.07%	57.02%	57.35%

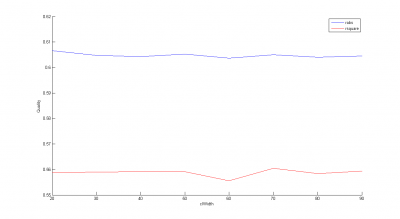
Зависимость от 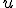$u$

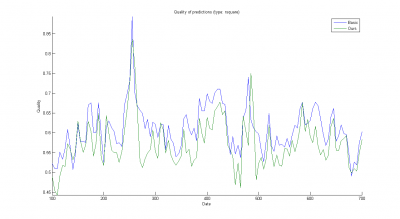
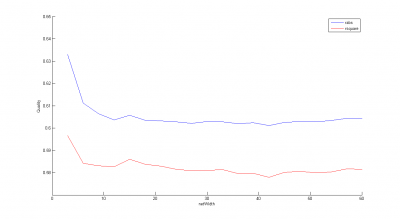
При варьировании $u$ верхняя граница обучающей выборки $t_{max}$ последовательно принимала 13 значений с интервалом в 50 дней. Величина $u$ менялась от 20 до 90 с шагом 10 дней. Полагалось $w = 10$ , $v = 35$ , $K = 4$ . Результаты — на рисунке ниже (промо-акции оставлены; при обнулении результаты мало отличаются).

Видно, что качество прогнозов мало зависит от количества кластеров и $u$ . Это связано с «проклятием размерности» и несовершенством выбранной для кластеризации метрики.

Отчет о полученных результатах

Список литературы

P. Cortez, M. Rocha, J.Neves. Time Series Forecasting ARMA Models.
R. Nochai, T. Nochai. Model for Forecasting Oil Palm Price.
F. M. Thiesing, O. Vornberger. Sales Using Neural Networks.
I. A. Gheyas, L. S. Smith. Neural Network Approach to Time Series Forecasting.

Данная статья была создана в рамках учебного задания.

Студент: Алексей Островский

Преподаватель: В.В. Стрижов

Срок: 15 декабря 2009

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%BE%D0%B1%D1%8A%D0%B5%D0%BC%D0%BE%D0%B2_%D0%BF%D1%80%D0%BE%D0%B4%D0%B0%D0%B6_%D0%B3%D1%80%D1%83%D0%BF%D0%BF_%D1%82%D0%BE%D0%B2%D0%B0%D1%80%D0%BE%D0%B2_%28%D0%BE%D1%82%D1%87%D0%B5%D1%82%29»

Категории: Прогнозирование | Практика и вычислительные эксперименты

@@ Строка 256: / Строка 256: @@
 == Описание системы ==
-* Описание системы: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Ostrovskiy2009Groups/Docs/Systemdocs_Groups.doc].
+* Описание системы: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Ostrovskiy2009Groups/Docs/Systemdocs_Groups.doc].
-* Файлы системы находятся в папке [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Ostrovskiy2009Groups].
+* Файлы системы находятся в папке [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Ostrovskiy2009Groups].
 == Отчет о вычислительных экспериментах ==

Прогнозирование объемов продаж групп товаров (отчет)

Материал из MachineLearning.

Текущая версия

Описание проекта

Цель проекта

Обоснование проекта

Описание данных

Критерии качества

Требования к проекту

Выполнимость проекта

Используемые методы

Постановка задачи

Описание алгоритмов

Обзор литературы

Базовые предположения

Математическое описание

Варианты или модификации

Ширина окна при усреднении

Дискретное количество товаров

Оценки качества

Кластеризация магазинов

Работа с промо-акциями

Описание системы

Отчет о вычислительных экспериментах

Сравнение алгоритма с базовым

Зависимость работы алгоритма от параметров

Зависимость от способа округления

Зависимость от $v$ и $w$

Зависимость от количества кластеров $K$

Зависимость от $u$

Отчет о полученных результатах

Список литературы

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты

Прогнозирование объемов продаж групп товаров (отчет)

Материал из MachineLearning.

Текущая версия

Описание проекта

Цель проекта

Обоснование проекта

Описание данных

Критерии качества

Требования к проекту

Выполнимость проекта

Используемые методы

Постановка задачи

Описание алгоритмов

Обзор литературы

Базовые предположения

Математическое описание

Варианты или модификации

Ширина окна при усреднении

Дискретное количество товаров

Оценки качества

Кластеризация магазинов

Работа с промо-акциями

Описание системы

Отчет о вычислительных экспериментах

Сравнение алгоритма с базовым

Зависимость работы алгоритма от параметров

Зависимость от способа округления

Зависимость от и

Зависимость от количества кластеров

Зависимость от

Отчет о полученных результатах

Список литературы

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты

Зависимость от $v$ и $w$

Зависимость от количества кластеров $K$

Зависимость от $u$