Однослойный персептрон (пример)
Материал из MachineLearning.
(→Постановка задачи линейного разделения классов) |
(→Исходный код) |
||
| (4 промежуточные версии не показаны) | |||
| Строка 145: | Строка 145: | ||
== Исходный код == | == Исходный код == | ||
| - | Скачать листинги алгоритмов можно здесь [http://mlalgorithms.svn.sourceforge.net/ | + | Скачать листинги алгоритмов можно здесь [http://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Panov2009OneLayerPerceptron/]. |
== Смотри также == | == Смотри также == | ||
| Строка 157: | Строка 157: | ||
* Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006. | * Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006. | ||
| - | + | {{ЗаданиеВыполнено|Максим Панов|В.В.Стрижов|28 мая 2009|Maxx|Strijov}} | |
| - | + | ||
| - | + | ||
[[Категория:Линейные классификаторы]] | [[Категория:Линейные классификаторы]] | ||
[[Категория:Нейронные сети]] | [[Категория:Нейронные сети]] | ||
| + | [[Категория:Практика и вычислительные эксперименты]] | ||
Текущая версия
|
Однослойный персептрон — это линейный алгоритм классификации, принцип работы которого основан на модели нервной клетки - нейрона. Представляет собой пример нейронной сети с одним скрытым слоем.
Постановка задачи линейного разделения классов
Пусть - множество объектов;
- множество допустимых ответов. Будем считать, что
, где
- признаковое описание объекта, а
- дополнительный константный признак;
. Задана обучающая выборка
. Значения признаков
рассматриваются как импульсы, поступающие на вход нейрона, которые складываются с весами
. Если суммарный импульс превышает порог активации
, то нейрон возбуждается
и выдаёт на выходе 1, иначе выдаётся 0. Таким образом, нейрон вычисляет
-арную булеву функцию вида
Для настройки вектора весов воспользуемся методом стохастического градиента. Возьмем квадратичную функцию потерь: , а в качестве функции активации возьмем сигмоидную функцию:
. Согласно принципу минимизации эмпирического риска задача сводится к поиску вектора, доставляющего минимум функционалу
.
Описание алгоритма
В соотвествие с методом градиентного спуска:
где величина шага в направлении антиградиента, называемая также темпом обучения (learning rate). Темп обучения выбираем, решая задачу одномерной минимизации:
. Будем выбирать прецеденты
по одному в случайном порядке, для каждого делать градиентный шаг и сразу обновлять вектор весов:
Вычислительный эксперимент
Показана работа алгоритма в серии задач, основанных как на реальных, так и на модельных данных.
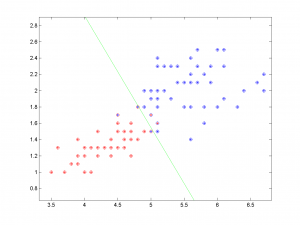
Пример на реальных данных: ирисы
Из задачи о классификации ирисов выбраны 2 вида ирисов: Versicolour и Virginica, которые предлагается классифицировать по двум признакам — длине и ширине лепестка. Данные содержат информацию о 50 цветках каждого видаiris.txt.
На графике показаны результаты классификации. По оси абсцисс отложено значение одного признака (длина лепестка в см.), а по оси ординат — значение второго признака (ширина лепестка в см.). Различные классы показаны крестиками различных цветов, а результат классификации показан кружочками соотвествующего цвета. Зеленой линией показана граница между классами, построенная алгоритмом.
%load data load 'iris.txt'; x = iris; x(:,1:2) = []; %eliminating first two attributes y = [repmat(0,50,1);repmat(1,50,1)]; %creating class labels %plotting data plot(x(y == 0,1),x(y == 0,2),'*r'); hold on plot(x(y == 1,1),x(y == 1,2),'*b'); %invoke One layer perceptron algorithm w = OneLayerPerc(x,y); %getting classification y = PercTest(x,w); %plotting resulting classification plot(x(y == 0,1),x(y == 0,2),'or'); plot(x(y == 1,1),x(y == 1,2),'ob'); plot([w(3)/w(1),0],[0,w(3)/w(2)],'g'); hold off;
Заметим, что данные линейно не разделимы, но алгоритм показывает хороший результат, допустив 5 ошибок классификации.
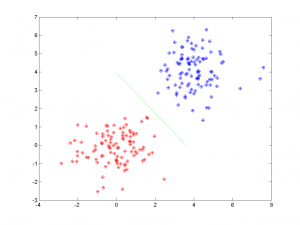
Модельные данные (простой вариант): 2 нормально распределенных класса линейно разделимы
%generating 2 sample normal classes x = GetNormClass(100,[0,0],[1,1]); s = GetNormClass(100,[4,4],[1,1]); x = [x;s]; y = [repmat(1,100,1);repmat(0,100,1)]; %invoke One layer perceptron algorithm w = OneLayerPerc(x,y); %generating control data with the same distribution x = GetNormClass(100,[0,0],[1,1]); s = GetNormClass(100,[4,4],[1,1]); x = [x;s]; %plotting control data plot(x(:,1),x(:,2),'*r'); hold on plot(s(:,1),s(:,2),'*b'); %getting classification y = PercTest(x,w); %plotting classified data plot(x(y == 0,1),x(y == 0,2),'ob'); plot(x(y == 1,1),x(y == 1,2),'or'); plot([w(3)/w(1),0],[0,w(3)/w(2)],'g'); hold off
Алгоритм не допустил при классификации ни одной ошибки.
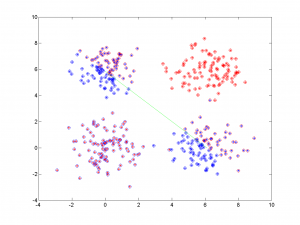
Модельные данные (сложный вариант): задача исключающего ИЛИ
%generate 2 sample classes x = GetNormClass(100,[0,0],[1,1]); s = GetNormClass(100,[6,6],[1,1]); x = [x;s]; s = GetNormClass(100,[0,6],[1,1]); x = [x;s]; s = GetNormClass(100,[6,0],[1,1]); x = [x;s]; y = [repmat(1,200,1);repmat(0,200,1)]; %invoke One layer perceptron algorithm w = OneLayerPerc(x,y); %generate control data with the same distribution x = GetNormClass(100,[0,0],[1,1]); s = GetNormClass(100,[6,6],[1,1]); x = [x;s]; s = GetNormClass(100,[0,6],[1,1]); x = [x;s]; s = GetNormClass(100,[6,0],[1,1]); x = [x;s]; %plot control data plot(x(y == 1,1),x(y == 1,2),'*r'); hold on plot(x(y == 0,1),x(y == 0,2),'*b'); %get classification y = PercTest(x,w); %plot classified data plot(x(y == 0,1),x(y == 0,2),'ob'); plot(x(y == 1,1),x(y == 1,2),'or'); plot([w(3)/w(1),0],[0,w(3)/w(2)],'g'); hold off
Алгоритм допустил около 50% ошибок классификация, что неудивительно, т.к. входные данные были принципиально линейно неразделимы.
Исходный код
Скачать листинги алгоритмов можно здесь [1].
Смотри также
Литература
- Nabney Ian, NetLab Algotithms for Pattern Recognition. Springer. 2001.
- К. В. Воронцов, Лекции по линейным алгоритмам классификации
- Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |