Метод Бокса-Кокса

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 6: Строка 6:
:<tex> y_i^{\lambda} = \begin{cases}\frac{y_i^\lambda-1}{\lambda},&\text{if } \lambda \neq 0,\\ \log{(y_i)},& \text{if } \lambda = 0.\end{cases}</tex>
:<tex> y_i^{\lambda} = \begin{cases}\frac{y_i^\lambda-1}{\lambda},&\text{if } \lambda \neq 0,\\ \log{(y_i)},& \text{if } \lambda = 0.\end{cases}</tex>
-
Параметр можно выбирать <tex>\lambda</tex>, максимизируя логарифм правдоподобия.
+
Параметр <tex>\lambda</tex> можно выбирать, максимизируя логарифм правдоподобия.
Еще один способ поиска оптимального значения параметра основан на поиске максимальной величины коэффициента корреляции между квантилями функции нормального распределения и отсортированной преобразованной последовательностью.
Еще один способ поиска оптимального значения параметра основан на поиске максимальной величины коэффициента корреляции между квантилями функции нормального распределения и отсортированной преобразованной последовательностью.

Версия 22:22, 28 декабря 2013

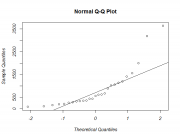
В реальности часто приходится иметь дело со статистическими данными, которые по тем или иным причинам не проходят тест на нормальность. В этой ситуации есть два выхода: либо обратиться к непараметрическим методам, либо воспользоваться специальными методами, позволяющими преобразовать исходную «ненормальную статистику» в «нормальную». Среди множества таких методов преобразований одним из лучших (при неизвестном типе распределения) считается преобразование Бокса-Кокса.

Содержание

Вид преобразования

Для исходной последовательности y = \{ y_1, \ldots, y_n \}, \quad y_i > 0, \quad i = 1,\ldots,n однопараметрическое преобразование Бокса-Кокса с параметром \lambda определяется следующим образом:

y_i^{\lambda} = \begin{cases}\frac{y_i^\lambda-1}{\lambda},&\text{if } \lambda \neq 0,\\ \log{(y_i)},& \text{if } \lambda = 0.\end{cases}

Параметр \lambda можно выбирать, максимизируя логарифм правдоподобия. Еще один способ поиска оптимального значения параметра основан на поиске максимальной величины коэффициента корреляции между квантилями функции нормального распределения и отсортированной преобразованной последовательностью.

Модификации

Так как исходный метод предполагает работу только с положительными величинами, было предложено несколько модификаций, учитывающих нулевые и отрицательные значения.

Самый очевидный вариант - сдвиг всех значений на константу \alpha так, чтобы выполнялось условие \quad (y_i + \lambda_2)> 0, \quad i = 1,\ldots,n. После этого преобразование выглядит так:

y_i^{\lambda} = \begin{cases}\frac{(y_i+\alpha)^{\lambda}-1}{\lambda},&\text{if } \lambda_1 \neq 0,\\ \log{(y_i+\alpha)},& \text{if } \lambda = 0.\end{cases}

Еще более общая форма:

\tau(y_i;\lambda, \alpha) = \begin{cases} \frac{(y_i + \alpha)^\lambda - 1}{\lambda (\operatorname{GM}(y))^{\lambda - 1}}, & \text{if } \lambda\neq 0, \\ \operatorname{GM}(y)\ln(y_i + \alpha), & \text{if } \lambda=0,\end{cases}

где \quad \operatorname{GM}(y) = (y_1\cdots y_n)^{1/n}.

Пример

qqplot для исходных данных.
qqplot для исходных данных.
Графики статистик для всех использованных тестов на нормальность.
Графики статистик для всех использованных тестов на нормальность.
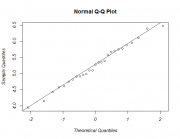
qqplot для данных, преобразованных методом Бокса-Кокса с .
qqplot для данных, преобразованных методом Бокса-Кокса с \lambda=-0.06.

В системе R с использованием пакета AID: 

> data = textile[,1]
> shapiro.test(data)
Shapiro-Wilk normality test
data:  data
W = 0.7604, p-value = 3.031e-05
> bctr = boxcoxnc(data)
> bctr$result
              sw    ad  cvm   pt    sf    lt    jb          ac
lambda.hat -0.06 -0.08 -0.1 0.02 -0.06 -0.06 -0.06 -0.04866667
sw.pvalue   1.00  1.00  1.0 1.00  1.00  1.00  1.00  1.00000000
sf.pvalue   1.00  1.00  1.0 1.00  1.00  1.00  1.00  1.00000000
jb.pvalue   1.00  1.00  1.0 1.00  1.00  1.00  1.00  1.00000000

Реализации

  • MATLAB: функция boxcox из Financial toolbox.
  • R: функция boxcox для линейных моделей в пакете MASS, boxcoxnc в пакете AID, box.cox в пакете car.

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%91%D0%BE%D0%BA%D1%81%D0%B0-%D0%9A%D0%BE%D0%BA%D1%81%D0%B0»
Личные инструменты