Расстояние Кука
Материал из MachineLearning.
м (→Ссылки) |
|||
| (24 промежуточные версии не показаны) | |||
| Строка 1: | Строка 1: | ||
| - | '''Расстояние Кука''' (Cook's distance) является широко используемым методом оценки влияния соответствующего наблюдения (элемента выборки) на уравнение регрессии. Эта величина показывает разницу между вычисленными коэффициентами уравнения регрессии и значениями, которые получились бы при исключении соответствующего наблюдения. В адекватной модели все расстояния Кука должны быть примерно одинаковыми; если это не так, то имеются основания считать, что соответствующее наблюдение (или наблюдения) смещает оценки коэффициентов регрессии. | + | '''Расстояние Кука''' (Cook's distance) является широко используемым методом оценки влияния соответствующего наблюдения (элемента выборки) на уравнение [[Регрессия|регрессии]]. Эта величина показывает разницу между вычисленными коэффициентами уравнения регрессии и значениями, которые получились бы при исключении соответствующего наблюдения. В адекватной модели все расстояния Кука должны быть примерно одинаковыми; если это не так, то имеются основания считать, что соответствующее наблюдение (или наблюдения) смещает оценки коэффициентов регрессии. |
| - | Метод назван в честь американского | + | Метод назван в честь американского ученого [http://users.stat.umn.edu/~rdcook/ Р. Денниса Кука] , который ввел данное понятие в 1977 году. |
== Определение == | == Определение == | ||
| + | Расстояние Кука оценивает эффект от удаления одного (рассматриваемого) наблюдения и вычисляется по следующей формуле: | ||
| + | |||
| + | ::<tex> D_i = \frac{ \sum_{j=1}^n (\hat Y_j\ - \hat Y_{j(i)})^2 }{p \ \mathrm{MSE}}, </tex> | ||
| + | |||
| + | где | ||
| + | |||
| + | <tex>\hat Y_j</tex> — предсказание регрессионной модели, построенной по всей выборке, получаемое для <tex>j</tex>-ого наблюдения, | ||
| + | |||
| + | <tex>\hat Y_{j(i)}</tex> — предсказание регрессионной модели, построенной по выборке без <tex>i</tex>-ого наблюдения, получаемое для <tex>j</tex>-ого наблюдения, | ||
| + | |||
| + | <tex>p</tex> — количество параметров модели, | ||
| + | |||
| + | <tex> \mathrm{MSE} </tex> — среднеквадратичная ошибка модели. | ||
| + | |||
| + | == Нахождение и удаление выбросов == | ||
| + | |||
| + | Существуют различные подходы к определению выбросов с помощью расстояния Кука. | ||
| + | |||
| + | Самый простой способ нахождения это порог <tex> D_i > 1 </tex> <ref name="heij">Cook, R. Dennis; and Weisberg, Sanford (1982); Residuals and influence in regression, New York, NY: Chapman & Hall.</ref> | ||
| + | |||
| + | Наиболее распространенной эвристикой считается <tex> D_i > 4/n </tex>, где <tex>n</tex> — количество наблюдений в выборке. <ref name="two"> Bollen, Kenneth A.; and Jackman, Robert W. (1990); Regression diagnostics: An expository treatment of outliers and influential cases , in Fox, John; and Long, J. Scott (eds.); Modern Methods of Data Analysis (pp. 257-91). </ref> | ||
| + | |||
| + | == Пример использования == | ||
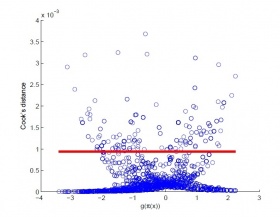
| + | [[Изображение:Cook.jpg|280px|thumb|Визуализация наблюдений с помощью расстояния Кука. Красным обозначен уровень 4/n, где n — количество наблюдений (n = 206).]] | ||
| + | |||
| + | Рассмотрим задачу по оценке [http://www.machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2013#.D0.AD.D1.84.D1.84.D0.B5.D0.BA.D1.82.D0.B8.D0.B2.D0.BD.D0.BE.D1.81.D1.82.D1.8C_.D1.82.D1.80.D0.BE.D0.BC.D0.B1.D0.BE.D0.BB.D0.B8.D1.82.D0.B8.D1.87.D0.B5.D1.81.D0.BA.D0.BE.D0.B9_.D1.82.D0.B5.D1.80.D0.B0.D0.BF.D0.B8.D0.B8 эффективность тромболитической терапии]. В данной задаче собраны данные по 206 пациентам второго кардиологического отделения московской городской клинической больницы №25. Имеются результаты 14 анализов, а также 8 дополнительных признаков, описывающих пациента (пол, возраст, курение, наличие диабета и т.д.). | ||
| + | Построив уравнение регрессии и оценив расстояние Кука, мы можем визуализировать наблюдения и определить выбросы. | ||
| + | |||
| + | == Реализации == | ||
| + | |||
| + | * MATLAB: В версии 2013b и выше реализован отдельный класс для [http://www.mathworks.com/help/stats/generalizedlinearmodelclass.html обобщенной модели регрессии]. | ||
| + | Построив модель с помощью функции [http://www.mathworks.com/help/stats/fitglm.html#outputarg_mdl mdl = fitglm(X, y)], можем оценить для всех наблюдений расстояние Кука с помощью функций класса: mdl.Diagnostics.CooksDistance. | ||
| + | |||
| + | * R: в пакете [http://stat.ethz.ch/R-manual/R-patched/library/stats/html/stats-package.html stats] реализован метод для оценки расстояния Кука для уже настроенной модели cooks.distance(model, ...). | ||
| + | |||
| + | == Ссылки == | ||
| + | |||
| + | <references /> | ||
| + | |||
| + | * Cook, R. Dennis (February 1977). [http://www.jstor.org/discover/10.2307/1268249?uid=3738032&uid=2&uid=4&sid=21103080796681 "Detection of Influential Observations in Linear Regression"]. | ||
| + | |||
| + | * [http://www.mathworks.com/help/stats/generalizedlinearmodelclass.html GeneralizedLinearModel class]. MATLAB R2013b Documentation. | ||
| Строка 11: | Строка 53: | ||
[[Категория:Прикладная статистика]] | [[Категория:Прикладная статистика]] | ||
| + | [[Категория:Регрессионный анализ]] | ||
Текущая версия
Расстояние Кука (Cook's distance) является широко используемым методом оценки влияния соответствующего наблюдения (элемента выборки) на уравнение регрессии. Эта величина показывает разницу между вычисленными коэффициентами уравнения регрессии и значениями, которые получились бы при исключении соответствующего наблюдения. В адекватной модели все расстояния Кука должны быть примерно одинаковыми; если это не так, то имеются основания считать, что соответствующее наблюдение (или наблюдения) смещает оценки коэффициентов регрессии.
Метод назван в честь американского ученого Р. Денниса Кука , который ввел данное понятие в 1977 году.
Содержание |
Определение
Расстояние Кука оценивает эффект от удаления одного (рассматриваемого) наблюдения и вычисляется по следующей формуле:
где
— предсказание регрессионной модели, построенной по всей выборке, получаемое для
-ого наблюдения,
— предсказание регрессионной модели, построенной по выборке без
-ого наблюдения, получаемое для
-ого наблюдения,
— количество параметров модели,
— среднеквадратичная ошибка модели.
Нахождение и удаление выбросов
Существуют различные подходы к определению выбросов с помощью расстояния Кука.
Самый простой способ нахождения это порог [1]
Наиболее распространенной эвристикой считается , где
— количество наблюдений в выборке. [1]
Пример использования
Рассмотрим задачу по оценке эффективность тромболитической терапии. В данной задаче собраны данные по 206 пациентам второго кардиологического отделения московской городской клинической больницы №25. Имеются результаты 14 анализов, а также 8 дополнительных признаков, описывающих пациента (пол, возраст, курение, наличие диабета и т.д.). Построив уравнение регрессии и оценив расстояние Кука, мы можем визуализировать наблюдения и определить выбросы.
Реализации
- MATLAB: В версии 2013b и выше реализован отдельный класс для обобщенной модели регрессии.
Построив модель с помощью функции mdl = fitglm(X, y), можем оценить для всех наблюдений расстояние Кука с помощью функций класса: mdl.Diagnostics.CooksDistance.
- R: в пакете stats реализован метод для оценки расстояния Кука для уже настроенной модели cooks.distance(model, ...).
Ссылки
- Cook, R. Dennis (February 1977). "Detection of Influential Observations in Linear Regression".
- GeneralizedLinearModel class. MATLAB R2013b Documentation.