Частичная автокорреляция

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Описание)
 
(11 промежуточных версий не показаны.)
Строка 1: Строка 1:
{{TOCright}}
{{TOCright}}
-
'''Частичная (частная) автокорреляция''' (partial autocorrelation) временных рядов используется для нахождения периодичностей во временных рядах.
+
'''Частичная (частная) автокорреляция''' (partial autocorrelation) временных рядов используется для нахождения периодичностей во [[Временной_ряд|временных рядах]] и нахождения порядка авторегрессионной модели ряда.
-
==Определение==
+
==Описание==
 +
 
 +
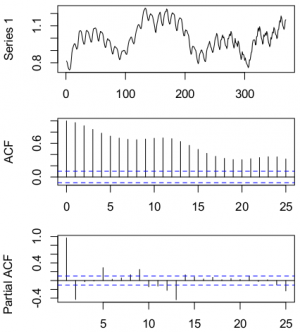
[[Изображение:Ml_im.png|thumb|right|300px|На графиках представлен пример временного ряда, его автокоррелиционная функция и его частичная автокорреляционная функция (сверху вниз).]]
Допустим дан временной ряд <tex>y_i</tex>. Частичную автокорреляцию для лага <tex>k</tex> обозначим за <tex>pacf(k)</tex>. Тогда
Допустим дан временной ряд <tex>y_i</tex>. Частичную автокорреляцию для лага <tex>k</tex> обозначим за <tex>pacf(k)</tex>. Тогда
<tex>pacf(k)=\left\{\begin{array}{ccccccccccc}
<tex>pacf(k)=\left\{\begin{array}{ccccccccccc}
-
corr(y_{t+k}, y_t) , k=1\\
+
corr(y_{t+k}, y_t) , k=1,\\
-
corr(y_{t+k} - y_{t+k}^{k-1}, y_t - y_t^{k-1}),k>1
+
corr(y_{t+k} - y_{t+k}^{k-1}, y_t - y_t^{k-1}),k>1,
-
\end{array}\right.,</tex>
+
\end{array}\right.</tex>
-
где <tex>y_t^{k-1}</tex> - линейная регрессия на <tex>y_{t+1}, y_{t+2}, \dots , y_{t+k-1}</tex>, т.е.
+
где <tex>y_t^{k-1}</tex> -- линейная регрессия на <tex>y_{t+1}, y_{t+2}, \dots , y_{t+k-1}</tex>, т.е.
<tex>y^{k-1}_t = \beta_1 y_{t+1} + \beta_2 y_{t+2} + \dots + \beta_{k-1} y_{t+k-1}</tex> и
<tex>y^{k-1}_t = \beta_1 y_{t+1} + \beta_2 y_{t+2} + \dots + \beta_{k-1} y_{t+k-1}</tex> и
-
<tex>y^{k-1}_{t+k} = \beta_1 y_{t+h-1} + \beta_2 y_{t+h-2} + \dots + \beta_{h-1} y_{t+1}</tex>
+
<tex>y^{k-1}_{t+k} = \beta_1 y_{t+k-1} + \beta_2 y_{t+k-2} + \dots + \beta_{k-1} y_{t+1}</tex>.
-
 
+
-
==Описание==
+
-
Частичная автокорреляция похожа на обычную автокорреляцию, однако дополнительно удаляет линейную зависимость между cдвинутыми рядами путем вычитания <tex>y^{k-1}_t</tex> и <tex>y^{k-1}_{t+k}</tex>.
+
Частичная автокорреляция похожа на обычную [[Автокорреляция|автокорреляцию]], однако дополнительно удаляет линейную зависимость между cдвинутыми рядами путем вычитания <tex>y^{k-1}_t</tex> и <tex>y^{k-1}_{t+k}</tex>, как описано выше.
-
[[Изображение:Ml_im.png|thumb|right|300px|На графиках представлен пример временного ряда, его автокоррелиционная функция и его частичная автокорреляционная функция.]]
 
==Программные реализации==
==Программные реализации==

Текущая версия

Содержание

Частичная (частная) автокорреляция (partial autocorrelation) временных рядов используется для нахождения периодичностей во временных рядах и нахождения порядка авторегрессионной модели ряда.

Описание

На графиках представлен пример временного ряда, его автокоррелиционная функция и его частичная автокорреляционная функция (сверху вниз).
На графиках представлен пример временного ряда, его автокоррелиционная функция и его частичная автокорреляционная функция (сверху вниз).

Допустим дан временной ряд y_i. Частичную автокорреляцию для лага k обозначим за pacf(k). Тогда

pacf(k)=\left\{\begin{array}{ccccccccccc} corr(y_{t+k}, y_t) , k=1,\\ corr(y_{t+k} - y_{t+k}^{k-1}, y_t - y_t^{k-1}),k>1, \end{array}\right.

где y_t^{k-1} -- линейная регрессия на y_{t+1}, y_{t+2}, \dots , y_{t+k-1}, т.е.

y^{k-1}_t = \beta_1 y_{t+1} + \beta_2 y_{t+2} + \dots + \beta_{k-1} y_{t+k-1} и

y^{k-1}_{t+k} = \beta_1 y_{t+k-1} + \beta_2 y_{t+k-2} + \dots + \beta_{k-1} y_{t+1}.

Частичная автокорреляция похожа на обычную автокорреляцию, однако дополнительно удаляет линейную зависимость между cдвинутыми рядами путем вычитания y^{k-1}_t и y^{k-1}_{t+k}, как описано выше.


Программные реализации

Ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A7%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%BD%D0%B0%D1%8F_%D0%B0%D0%B2%D1%82%D0%BE%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB%D1%8F%D1%86%D0%B8%D1%8F»
Личные инструменты