Теорема схемы
Материал из MachineLearning.
(ссылки, оформление) |
|||
| (11 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | '''Теорема схемы''' (англ. schema theorem) | + | '''Теорема схемы''' (англ. schema theorem) — теорема, описывающее действие [[Генетический алгоритм|генетического алгоритма]] через понятие схемы. Каждой схеме соответствует некоторое подмножество особей в популяции. При определенных условиях, оговариваемых в теореме, будет выполняться экспоненциальный рост числа особей в этом подмножестве. Теорема была предложена Холландом, и это была первая успешная попытка объяснить действие генетического алгоритма. |
__TOC__ | __TOC__ | ||
| - | ==Формулировка теоремы== | + | == Формулировка теоремы == |
| - | ===Предположения и обозначения=== | + | |
| - | Пусть используется простой генетический алгоритм, | + | === Предположения и обозначения === |
| + | Пусть используется простой генетический алгоритм, то есть ГА с одноточечным кроссинговером и одноточечной мутацией. | ||
Будем считать, что особью в популяции является бинарная строка длины <tex>l</tex>. Если это не так, всегда можно закодировать ее нужным образом. | Будем считать, что особью в популяции является бинарная строка длины <tex>l</tex>. Если это не так, всегда можно закодировать ее нужным образом. | ||
Введем следующие понятия: | Введем следующие понятия: | ||
| - | * | + | * Схема — слово длины <tex>l</tex> в алфавите <tex>\{0,1,*\}</tex>, где <tex>*</tex> имеет смысл любого из символов <tex>\{0,1\}</tex>. В дальнейшем схема будет обозначаться <tex>H</tex>; |
| - | * Пример | + | * Пример схемы — особь, удовлетворяющая схеме. Например, если схемой является <tex>0*1</tex>, то особь <tex>001</tex> является примером, а особь <tex>000</tex> — нет. Число примеров схемы H в обрабатываемой алгоритмом популяции в момент времени <tex>t</tex> (то есть число особей популяции, удовлетворяющих схеме) будем обозначать как <tex>m(H,t)</tex>; |
| - | * Порядок схемы <tex>o(H)</tex> | + | * Порядок схемы <tex>o(H)</tex> — число символов в схеме, не равных <tex>*</tex>; |
| - | * Определяющая длина схемы <tex>\delta(H)</tex> | + | * Определяющая длина схемы <tex>\delta(H)</tex> — расстояние между крайними символами, не равными <tex>*</tex>; |
| - | * Степень приспособленности схемы <tex>f(H,t)</tex> | + | * Степень приспособленности схемы <tex>f(H,t)</tex> — средняя степень приспособлености по всем примерам схемы <tex>H</tex> в популяции в момент времени <tex>t</tex>; |
| - | * Средняя приспособленность всей | + | * Средняя приспособленность всей популяции — <tex>f_e(t)</tex>; |
| - | * <tex>P_m</tex> | + | * <tex>P_m</tex> — вероятность мутации; |
| - | * <tex>P_c</tex> | + | * <tex>P_c</tex> — вероятность кроссинговера. |
| - | ===Теорема=== | + | |
| - | <tex> | + | === Теорема === |
| - | ==Интерпретация теоремы== | + | <tex>\mathbb{E} m(H,t+1) \ge m(H,t)\: \frac{f(H,t)}{f_e(t)} \: \left( 1-\frac{P_c\delta(H)}{l-1}-o(H)P_m \right).</tex> |
| - | Пусть имеется какая-то начальная популяция. Рассмотрим некоторую схему небольшого порядка с небольшим определяющим расстоянием, степень приспособленности которой больше, чем в среднем по данной популяции. Тогда количество примеров этой схемы в последующих популяциях будет расти экспоненциально | + | |
| - | ==Гипотеза строительных блоков (building block hypothesis)== | + | == Интерпретация теоремы == |
| - | Была предложена Гольдбергом в 1989 году. Строительный | + | Пусть имеется какая-то начальная популяция. Рассмотрим некоторую схему небольшого порядка с небольшим определяющим расстоянием, степень приспособленности которой больше, чем в среднем по данной популяции. Тогда количество примеров этой схемы в последующих популяциях будет расти экспоненциально на протяжении некоторого числа популяций. Таким образом, «хорошие» в смысле приспособленности схемы (с дополнительными ограничениями на <tex>o(H)</tex> и <tex>\delta(H)</tex>) сохраняются и покрывают все большую часть популяции. При этом дополнительные ограничения диктуются следующими соображениями: мутации реже разрушают схемы меньшего порядка, а кроссинговер реже разрушает схемы с меньшей определяющей длиной. |
| + | |||
| + | == Гипотеза строительных блоков (building block hypothesis) == | ||
| + | Была предложена Гольдбергом в 1989 году. Строительный блок — схема, обладающая следующими свойствами: | ||
# Высокой приспособленностью | # Высокой приспособленностью | ||
# Низким порядком | # Низким порядком | ||
# Короткой определяющей длиной | # Короткой определяющей длиной | ||
| - | Как показывает теорема схем, такие блоки экспоненциально увеличивают количество примеров по мере работы алгоритма. В связи с этим была высказана гипотеза, что | + | Как показывает теорема схем, такие блоки экспоненциально увеличивают количество примеров по мере работы алгоритма. В связи с этим была высказана гипотеза, что «строительные блоки объединяются, чтобы сформировать лучшие блоки». Таким образом, рекомбинация и экспоненциальных рост примеров блоков ведет к формированию лучших блоков, которые в конечном итоге дадут решение (решение будет примером самой лучшей схемы-блока). Поэтому можно говорить о том, что ГА ведет поиск на множестве строительных блоков. |
| - | ===Критика=== | + | |
| + | === Критика === | ||
Гипотеза строительных блоков не является формальным математическим утверждением. Вот некоторые аргументы, опровергающие ее: | Гипотеза строительных блоков не является формальным математическим утверждением. Вот некоторые аргументы, опровергающие ее: | ||
# Теорема схем описывает увеличение количества примеров только в следующем поколении. Далее может измениться приспособленность схемы и популяции, и увеличение может смениться уменьшением. | # Теорема схем описывает увеличение количества примеров только в следующем поколении. Далее может измениться приспособленность схемы и популяции, и увеличение может смениться уменьшением. | ||
| - | # Строго говоря, утверждение теоремы схем носит вероятностный характер (в левой части неравенства стоит математическое ожидание). Поэтому возможны отклонения от этого закона, а насколько они велики и | + | # Строго говоря, утверждение теоремы схем носит вероятностный характер (в левой части неравенства стоит математическое ожидание). Поэтому возможны отклонения от этого закона, а насколько они велики и вероятны — в теореме не указано. |
| - | # Комбинация двух | + | # Комбинация двух «хороших» строительных блоков не всегда является «хорошей». Существуют примеры, когда такое комбинирование приводит к существенному снижению приспособленности схемы-блока. |
Тем не менее, иногда гипотеза строительных блоков выполняется на практике. Далее следует пример. | Тем не менее, иногда гипотеза строительных блоков выполняется на практике. Далее следует пример. | ||
| - | ==Задача выбора признаков с помощью ГА== | + | |
| - | ===Предварительные замечания=== | + | == Задача выбора признаков с помощью ГА == |
| - | Суть данной задачи ( см. [[Выбор признаков с помощью генетических алгоритмов (пример)]] ) позволяет предположить, что гипотеза строительных блоков выполняется. Действительно, схемы соответствуют наборам признаков. Тогда | + | === Предварительные замечания === |
| - | ===Постановка вычислительного эксперимента=== | + | Суть данной задачи (см. [[Выбор признаков с помощью генетических алгоритмов (пример)]]) позволяет предположить, что гипотеза строительных блоков выполняется. Действительно, схемы соответствуют наборам признаков. Тогда в большинстве случаев комбинация хороших наборов должна дать хороший набор. |
| - | Данные порождались следующим образом ( | + | |
| + | === Постановка вычислительного эксперимента === | ||
| + | Данные порождались следующим образом (D — дисперсия, D=100): | ||
<source lang="matlab"> | <source lang="matlab"> | ||
x = [ 1:0.5:20 ]'; | x = [ 1:0.5:20 ]'; | ||
y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + sqrt( D ) * randn( size( x, 1 ), 1 ); | y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + sqrt( D ) * randn( size( x, 1 ), 1 ); | ||
</source> | </source> | ||
| - | Выборка делилась на training и testing части в соотношении | + | Выборка делилась на training и testing части в соотношении 60 %:40 % случайным образом. |
Использовался следующий набор порождающих функций (всего 12): <br /> | Использовался следующий набор порождающих функций (всего 12): <br /> | ||
<tex>1,\; x,\; x^2,\; log(x),\; x^3,\; x*log(x),\; x^4,\; x^2*log(x),\; x^2*cos(x),\; cos(x)*log(x),\; x*sin(x)*log(x),\; x^2*cos(x)*log(x).</tex> <br /> | <tex>1,\; x,\; x^2,\; log(x),\; x^3,\; x*log(x),\; x^4,\; x^2*log(x),\; x^2*cos(x),\; cos(x)*log(x),\; x*sin(x)*log(x),\; x^2*cos(x)*log(x).</tex> <br /> | ||
В наборе не было следующих функций, участвовавших в порождении: <tex>sin(x),\; x^2*sin(x).</tex> <br /> | В наборе не было следующих функций, участвовавших в порождении: <tex>sin(x),\; x^2*sin(x).</tex> <br /> | ||
| - | Задача решалась простым ГА. При этом менялось значение параметра Размер Популяции. Строились графики Диаметра Популяции от номера итерации. Под диаметром понимается первая норма ( | + | Задача решалась простым ГА. При этом менялось значение параметра Размер Популяции. Строились графики Диаметра Популяции от номера итерации. Под диаметром понимается первая норма (то есть сумма модулей компонент) вектора попарных Хемминговых расстояний между хромосомами в популяции. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | == | + | === Результаты === |
| + | [[Изображение:Diameter( number of generations ),PopulationSize=10N.png|600px]] <br /> | ||
| + | [[Изображение:Diameter( number of generations ),PopulationSize=15N.png|600px]] <br /> | ||
| + | [[Изображение:Diameter( number of generations ),PopulationSize=20N.png|600px]] <br /> | ||
| + | На всех 3 графиках четко виден резкий спад на первых 10-20 итерациях, а потом скачки. Эти скачки можно объяснить так: когда ГА сошелся к решению, все хромосомы очень похожы друг на друга в смысле Хеммингова расстояния, но если за счет мутации одна изменится, то расстояние до остальных станет одинаковым и ненулевым. Поэтому произойдет заметный скачок. <br /> | ||
| + | Видна закономерность в том, насколько резок спад: чем больше размер популяции, тем быстрее сходимость. | ||
| + | |||
| + | === Выводы === | ||
| + | Противоречий с гипотезой строительных блоков в данном случае нет. Наблюдается быстрое уменьшение диаметра популяции, что подтверждает сходимость к некоторой схеме. | ||
| + | |||
| + | == См. также == | ||
* [[Генетический алгоритм]] | * [[Генетический алгоритм]] | ||
* [[Выбор признаков с помощью генетических алгоритмов (пример)]] | * [[Выбор признаков с помощью генетических алгоритмов (пример)]] | ||
== Литература == | == Литература == | ||
| - | * | + | * Zbigniew Michalevicz, «Genetic Algorithms + Data Structures = Evolution Programs» (chapter 3: «GAs: Why Do They Work?»). |
| - | {{ | + | * Melanie Mitchell, «An Introduction to Genetic Algorithms». |
| + | {{ЗаданиеВыполнено|Nikolay Savinov|V.V.Strijov|20 июня 2010||strijov}} | ||
| + | |||
| + | [[Категория:Эволюционные алгоритмы]] | ||
Текущая версия
Теорема схемы (англ. schema theorem) — теорема, описывающее действие генетического алгоритма через понятие схемы. Каждой схеме соответствует некоторое подмножество особей в популяции. При определенных условиях, оговариваемых в теореме, будет выполняться экспоненциальный рост числа особей в этом подмножестве. Теорема была предложена Холландом, и это была первая успешная попытка объяснить действие генетического алгоритма.
Содержание |
Формулировка теоремы
Предположения и обозначения
Пусть используется простой генетический алгоритм, то есть ГА с одноточечным кроссинговером и одноточечной мутацией.
Будем считать, что особью в популяции является бинарная строка длины . Если это не так, всегда можно закодировать ее нужным образом.
Введем следующие понятия:
- Схема — слово длины
в алфавите
, где
имеет смысл любого из символов
. В дальнейшем схема будет обозначаться
;
- Пример схемы — особь, удовлетворяющая схеме. Например, если схемой является
, то особь
является примером, а особь
— нет. Число примеров схемы H в обрабатываемой алгоритмом популяции в момент времени
(то есть число особей популяции, удовлетворяющих схеме) будем обозначать как
;
- Порядок схемы
— число символов в схеме, не равных
;
- Определяющая длина схемы
— расстояние между крайними символами, не равными
;
- Степень приспособленности схемы
— средняя степень приспособлености по всем примерам схемы
в популяции в момент времени
;
- Средняя приспособленность всей популяции —
;
-
— вероятность мутации;
-
— вероятность кроссинговера.
Теорема
Интерпретация теоремы
Пусть имеется какая-то начальная популяция. Рассмотрим некоторую схему небольшого порядка с небольшим определяющим расстоянием, степень приспособленности которой больше, чем в среднем по данной популяции. Тогда количество примеров этой схемы в последующих популяциях будет расти экспоненциально на протяжении некоторого числа популяций. Таким образом, «хорошие» в смысле приспособленности схемы (с дополнительными ограничениями на и
) сохраняются и покрывают все большую часть популяции. При этом дополнительные ограничения диктуются следующими соображениями: мутации реже разрушают схемы меньшего порядка, а кроссинговер реже разрушает схемы с меньшей определяющей длиной.
Гипотеза строительных блоков (building block hypothesis)
Была предложена Гольдбергом в 1989 году. Строительный блок — схема, обладающая следующими свойствами:
- Высокой приспособленностью
- Низким порядком
- Короткой определяющей длиной
Как показывает теорема схем, такие блоки экспоненциально увеличивают количество примеров по мере работы алгоритма. В связи с этим была высказана гипотеза, что «строительные блоки объединяются, чтобы сформировать лучшие блоки». Таким образом, рекомбинация и экспоненциальных рост примеров блоков ведет к формированию лучших блоков, которые в конечном итоге дадут решение (решение будет примером самой лучшей схемы-блока). Поэтому можно говорить о том, что ГА ведет поиск на множестве строительных блоков.
Критика
Гипотеза строительных блоков не является формальным математическим утверждением. Вот некоторые аргументы, опровергающие ее:
- Теорема схем описывает увеличение количества примеров только в следующем поколении. Далее может измениться приспособленность схемы и популяции, и увеличение может смениться уменьшением.
- Строго говоря, утверждение теоремы схем носит вероятностный характер (в левой части неравенства стоит математическое ожидание). Поэтому возможны отклонения от этого закона, а насколько они велики и вероятны — в теореме не указано.
- Комбинация двух «хороших» строительных блоков не всегда является «хорошей». Существуют примеры, когда такое комбинирование приводит к существенному снижению приспособленности схемы-блока.
Тем не менее, иногда гипотеза строительных блоков выполняется на практике. Далее следует пример.
Задача выбора признаков с помощью ГА
Предварительные замечания
Суть данной задачи (см. Выбор признаков с помощью генетических алгоритмов (пример)) позволяет предположить, что гипотеза строительных блоков выполняется. Действительно, схемы соответствуют наборам признаков. Тогда в большинстве случаев комбинация хороших наборов должна дать хороший набор.
Постановка вычислительного эксперимента
Данные порождались следующим образом (D — дисперсия, D=100):
x = [ 1:0.5:20 ]'; y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + sqrt( D ) * randn( size( x, 1 ), 1 );
Выборка делилась на training и testing части в соотношении 60 %:40 % случайным образом.
Использовался следующий набор порождающих функций (всего 12):
В наборе не было следующих функций, участвовавших в порождении:
Задача решалась простым ГА. При этом менялось значение параметра Размер Популяции. Строились графики Диаметра Популяции от номера итерации. Под диаметром понимается первая норма (то есть сумма модулей компонент) вектора попарных Хемминговых расстояний между хромосомами в популяции.
Результаты
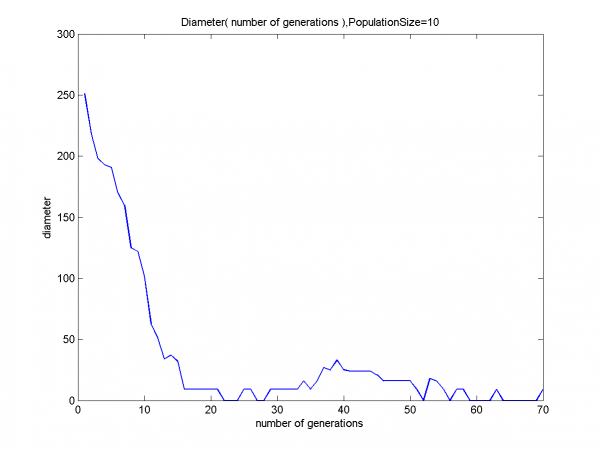
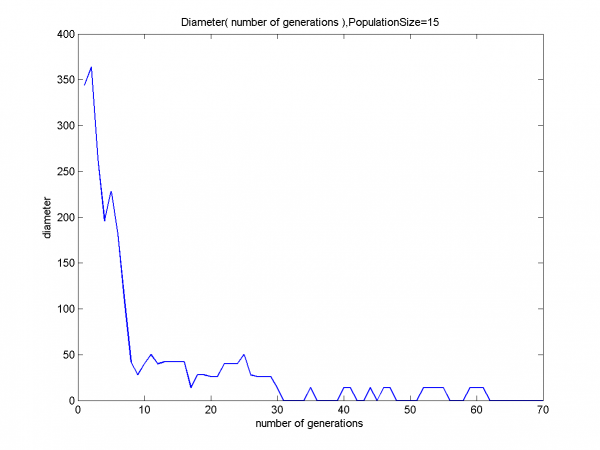
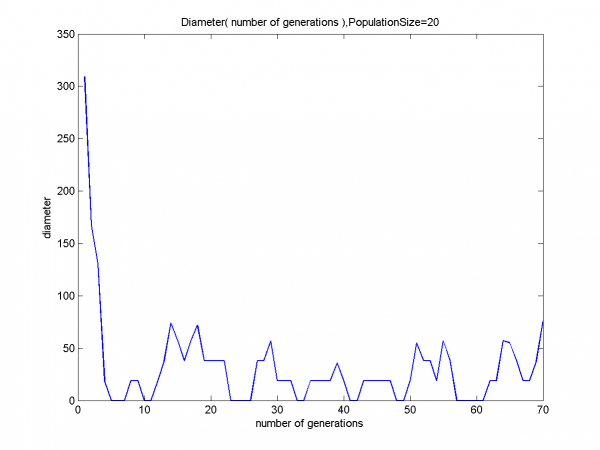
На всех 3 графиках четко виден резкий спад на первых 10-20 итерациях, а потом скачки. Эти скачки можно объяснить так: когда ГА сошелся к решению, все хромосомы очень похожы друг на друга в смысле Хеммингова расстояния, но если за счет мутации одна изменится, то расстояние до остальных станет одинаковым и ненулевым. Поэтому произойдет заметный скачок.
Видна закономерность в том, насколько резок спад: чем больше размер популяции, тем быстрее сходимость.
Выводы
Противоречий с гипотезой строительных блоков в данном случае нет. Наблюдается быстрое уменьшение диаметра популяции, что подтверждает сходимость к некоторой схеме.
См. также
Литература
- Zbigniew Michalevicz, «Genetic Algorithms + Data Structures = Evolution Programs» (chapter 3: «GAs: Why Do They Work?»).
- Melanie Mitchell, «An Introduction to Genetic Algorithms».
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |

