Биномиальное распределение
Материал из MachineLearning.
(дополнение) |
м |
||
| (37 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| + | {{Вероятностное распределение| | ||
| + | name =Биномиальное распределение| | ||
| + | type =Функция| | ||
| + | pdf_image =[[Изображение:Binomial distribution pmf.svg|325px]]| | ||
| + | cdf_image =[[Изображение:Binomial distribution cdf.svg|325px]]| | ||
| + | parameters =<tex>n \geq 0</tex> — число «испытаний»<br /><tex>0\leq p \leq 1</tex> — вероятность «успеха» | | ||
| + | support =<tex>k \in \{0,\ldots,n\}\!</tex>| | ||
| + | pdf =<tex>{n \choose k}\,p^k q^{n-k} \!</tex>| | ||
| + | cdf =<tex>I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!</tex>| | ||
| + | mean =<tex>np\!</tex>| | ||
| + | median =одно из <tex>\{[np]-1, [np], [np]+1\}</tex>| | ||
| + | mode =<tex>\lfloor (n+1)\,p\rfloor\!</tex>| | ||
| + | variance =<tex>npq\!</tex>| | ||
| + | skewness =<tex>\frac{1-2p}{\sqrt{npq}}\!</tex>| | ||
| + | kurtosis =<tex>\frac{1-6pq}{npq}\!</tex>| | ||
| + | entropy =<tex> \frac12 \log_2 \big( 2\pi e\, np(1-p) \big) + O \left( \frac{1}{n} \right) </tex>| | ||
| + | mgf =<tex>(q + pe^t)^n \!</tex>| | ||
| + | char =<tex>(q + pe^{it})^n \!</tex>| | ||
| + | }} | ||
| + | |||
==Определение== | ==Определение== | ||
| - | ''Биномиальное распределение'' | + | ''Биномиальное распределение'' — дискретное распределение вероятностей [[случайная_величина|случайной величины]] <tex>X,</tex> принимающей целочисленные значения <tex>k=0,1,\ldots,n</tex> с вероятностями: |
| - | + | ::<tex>P(X=k)={n \choose k}p^k(1-p)^{n-k}.</tex> | |
| - | Данное распределение характеризуется двумя параметрами: целым числом <tex>n>0</tex> | + | Данное распределение характеризуется двумя параметрами: целым числом <tex>n>0,</tex> называемым ''числом испытаний'', и вещественным числом <tex>p,</tex> <tex>0\le p\le 1,</tex> называемом ''вероятностью успеха в одном испытании''. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из <tex>n</tex> независимых испытаний, в каждом из которых может произойти "успех" с вероятностью <tex>p,</tex> то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы <tex>X=X_1+\cdots+X_n</tex> независимых слагаемых, имеющих [[распределение Бернулли]]. |
==Основные свойства== | ==Основные свойства== | ||
| - | [[Характеристическая функция]] <tex>\phi(t)=(1+p(e^{it}-1))^n</tex> | + | [[Характеристическая функция]]: <tex>\phi(t)=(1+p(e^{it}-1))^n.</tex> |
[[Моменты случайной величины|Моменты]]: | [[Моменты случайной величины|Моменты]]: | ||
| - | *Математическое ожидание: <tex>MX=np</tex> | + | *Математическое ожидание: <tex>MX=np.</tex> |
| - | *Дисперсия: <tex>DX=np(1-p)</tex> | + | *Дисперсия: <tex>DX=np(1-p).</tex> |
| - | *[[Асимметрия]]: <tex>\gamma_1=\frac{1-2p}{\sqrt{np(1-p)}}</tex> | + | *[[Асимметрия]]: <tex>\gamma_1=\frac{1-2p}{\sqrt{np(1-p)}};</tex> при <tex>p=0.5</tex> распределение симметрично относительно центра <tex>n/2.</tex> |
| - | ==Асимптотические приближения при больших n== | + | ==Асимптотические приближения при больших <tex>n</tex>== |
Если значения <tex>n</tex> велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. | Если значения <tex>n</tex> велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. | ||
| Строка 21: | Строка 41: | ||
===Приближение Пуассона=== | ===Приближение Пуассона=== | ||
| - | Приближение распределением Пуассона применяется в ситуациях, когда значения <tex>n</tex> большие, а значения <tex>p</tex> близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром <tex>\lambda=np</tex> | + | Приближение [[распределение Пуассона|распределением Пуассона]] применяется в ситуациях, когда значения <tex>n</tex> большие, а значения <tex>p</tex> близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром <tex>\lambda=np.</tex> |
| - | Строгая формулировка: если <tex>n\to\infty</tex> и <tex>p\to 0</tex> таким образом, что <tex>np\to\lambda</tex> | + | Строгая формулировка: если <tex>n\to\infty</tex> и <tex>p\to 0</tex> таким образом, что <tex>np\to\lambda,</tex> то |
| - | + | ::<tex>P(X=k)\to\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0, 1, 2, \ldots</tex> | |
| - | Более того, справедлива следующая оценка. Пусть <tex>Y</tex> | + | Более того, справедлива следующая оценка. Пусть <tex>Y</tex> — случайная величина, имеющая распределение Пуассона с параметром <tex>\lambda=np.</tex> |
Тогда для произвольного множества <tex>B\subset\{0,1,2,\ldots\}</tex> справедливо неравенство: | Тогда для произвольного множества <tex>B\subset\{0,1,2,\ldots\}</tex> справедливо неравенство: | ||
| - | + | ::<tex>|P(X\in B) - P(Y\in B)|\le 2np^2.</tex> | |
Доказательство и обзор более точных результатов, касающихся точности данного приближения, можно найти в [1, гл. III, §12]. | Доказательство и обзор более точных результатов, касающихся точности данного приближения, можно найти в [1, гл. III, §12]. | ||
===Нормальное приближение=== | ===Нормальное приближение=== | ||
| - | Приближение нормальным распределением используется в ситуациях, когда <tex>n\to\infty</tex> | + | Приближение нормальным распределением используется в ситуациях, когда <tex>n\to\infty,</tex> а <tex>p</tex> фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применение которой основано на представлении <tex>X</tex> в виде суммы <tex>n</tex> слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной величины |
| - | + | ::<tex>X'=\frac{X-MX}{\sqrt{DX}}=\frac{X-np}{\sqrt{npq},</tex> где <tex>q=1-p,</tex> | |
близко к стандартному нормальному. | близко к стандартному нормальному. | ||
===Локальная теорема Муавра-Лапласа=== | ===Локальная теорема Муавра-Лапласа=== | ||
| - | Данная теорема используется для приближенного вычисления вероятностей отдельных значений биномиального распределения. Она утверждает [1, гл. I, §6], что равномерно по всем значениям <tex>k</tex> | + | Данная теорема используется для приближенного вычисления вероятностей отдельных значений биномиального распределения. Она утверждает [1, гл. I, §6], что равномерно по всем значениям <tex>k,</tex> таким что <tex>|k-np|=o(npq)^{2/3},</tex> имеет место |
| - | + | ::<tex>P(X=k)\sim\frac{1}{\sqrt{2\pi npq}}e^{-\frac{(k-np)^2}{2npq}}=\frac{1}{\sqrt{npq}}\varphi\left(\frac{k-np}{\sqrt{npq}}\right),</tex> | |
| - | где <tex>\varphi</tex> | + | где <tex>\varphi</tex> — плотность стандартного нормального распределения. |
===Интегральная теорема Муавра-Лапласа=== | ===Интегральная теорема Муавра-Лапласа=== | ||
| - | На практике необходимость оценки вероятностей отдельных значений, которую дает локальная теорема Муавра-Лапласа, возникает | + | На практике необходимость оценки вероятностей отдельных значений, которую дает локальная теорема Муавра-Лапласа, возникает нечасто. Гораздо более важно оценивать вероятности событий, включающих в себя множество значений. Для этого используется интегральная теорема, которую можно сформулировать в следующем виде [1, гл. I, §6]: |
| - | + | ::<tex>\sup_{-\infty\le a<b\le\infty}\left|P\left(a<\frac{X-np}{\sqrt{npq}}\le b\right) - P(a<Z\le b)\right|\to 0</tex> при <tex>n\to\infty,</tex> | |
| - | где случайная величина <tex>Y</tex> имеет стандартное нормальное распределение <tex>\mathcal{N}(0,1)</tex> | + | где случайная величина <tex>Y</tex> имеет стандартное нормальное распределение <tex>\mathcal{N}(0,1),</tex> и аппроксимирующая вероятность определяется по формуле |
| - | + | ::<tex>P(a<Z\le b)=\Phi(b)-\Phi(a),</tex> | |
| - | где <tex>\Phi(t)</tex> | + | где <tex>\Phi(t)</tex> — функция распределения стандартного нормального закона: <tex>\Phi(t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^t e^{-t^2/2}\,dt.</tex> |
Есть ряд результатов, позволяющих оценить скорость сходимости. В [1, гл. I, §6] приводится следующий результат, являющийся частным случаем теоремы Берри-Эссеена: | Есть ряд результатов, позволяющих оценить скорость сходимости. В [1, гл. I, §6] приводится следующий результат, являющийся частным случаем теоремы Берри-Эссеена: | ||
| + | ::<tex>\sup_{-\infty\le x\le\infty}|F_n(x)-\Phi(x)|\le\frac{p^2+q^2}{\sqrt{npq}},</tex> | ||
| + | |||
| + | где <tex>F_n(x)</tex> — функция распределения случайной величины <tex>X'=\frac{X-np}{\sqrt{npq}}.</tex> На практике решение о том, насколько следует доверять нормальному приближению, принимают исходя из величины <tex>npq.</tex> Чем она больше, тем меньше будет погрешность приближения. | ||
| + | |||
| + | Заметим, что асимптотический результат не изменится, если заменить строгие неравенства на нестрогие и наоборот. Предельная вероятность от такой замены также не поменяется, так как нормальное распределение абсолютно непрерывно и вероятность принять любое конкретное значение для него равна нулю. Однако исходная вероятность от такой замены может измениться, что вносит в формулу некоторую неоднозначность. Для больших значений <tex>n</tex> изменение будет невелико, однако для небольших <tex>n</tex> это может внести дополнительную погрешность. | ||
| + | |||
| + | Для устранения этой неоднозначности, а также повышения точности приближения рекомендуется задавать интересующие события в виде интервалов с полуцелыми границами. При этом приближение получается точнее. Это связано с тем интуитивно понятным соображением, что аппроксимация кусочно-постоянной функции (функции распределения биномиального закона) с помощью непрерывной функции дает более точные приближения между точками разрыва, чем в этих точках. | ||
| + | |||
| + | ===Пример=== | ||
| + | |||
| + | Пусть <tex>n=20,</tex> <tex>p=0.5.</tex> Оценим вероятность того, что число успехов будет отличаться от наиболее вероятного значения <tex>10</tex> не более чем на <tex>3</tex>. Заметим, что значение <tex>npq=5</tex> очень мало, поэтому применение нормального приближения здесь довольно ненадежно. | ||
| + | |||
| + | Точная вероятность рассматриваемого события равна | ||
| + | |||
| + | ::<tex>P(7\le X\le 13)\approx 0.8846.</tex> | ||
| + | |||
| + | Применим нормальное приближение с той расстановкой неравенств, которая дана выше (снизу строгое, сверху нестрогое): | ||
| + | |||
| + | ::<tex>P(7\le X\le 13)=P(6<X\le 13)=P\left(\frac{6-10}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{13-10}{\sqrt{5}}\right)=P\left(-\frac{4}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{3}{\sqrt{5}}\right)\approx P\left(-\frac{4}{\sqrt{5}}<Z\le\frac{3}{\sqrt{5}}\right)=\Phi\left(\frac{3}{\sqrt{5}}\right) - \Phi\left(-\frac{4}{\sqrt{5}}\right)\approx 0.8733.</tex> | ||
| + | |||
| + | Ошибка приближения равна <tex>0.0113</tex>. | ||
| + | |||
| + | Теперь построим приближение, используя интервал с концами в полуцелых точках: | ||
| + | ::<tex>P(7\le X\le 13)=P(6.5<X< 13.5)=P\left(-\frac{3.5}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{3.5}{\sqrt{5}}\right)\approx P\left(-\frac{3.5}{\sqrt{5}}<Z\le\frac{3.5}{\sqrt{5}}\right)=\Phi\left(\frac{3.5}{\sqrt{5}}\right) - \Phi\left(-\frac{3.5}{\sqrt{5}}\right)\approx 0.8824.</tex> | ||
| + | |||
| + | Ошибка приближения равна <tex>0.0022</tex> — примерно в 5 раз меньше, чем в предыдущем подходе. | ||
==Литература== | ==Литература== | ||
| Строка 70: | Строка 116: | ||
|издательство = МЦНМО | |издательство = МЦНМО | ||
}} | }} | ||
| - | |||
== Ссылки == | == Ссылки == | ||
| Строка 76: | Строка 121: | ||
*[http://en.wikipedia.org/wiki/Binomial_distribution Binomial distribution] (Wikipedia) | *[http://en.wikipedia.org/wiki/Binomial_distribution Binomial distribution] (Wikipedia) | ||
| - | + | [[Категория:Вероятностные распределения]] | |
| - | + | ||
| - | [[Категория: | + | |
Текущая версия
Функция вероятности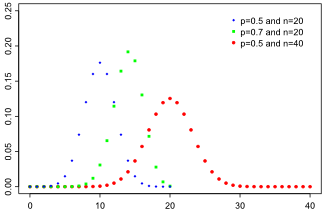
| |
Функция распределения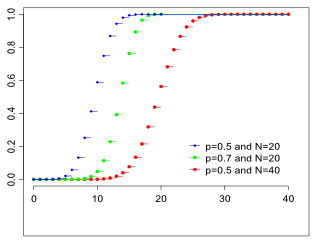
| |
| Параметры | |
| Носитель | |
| Функция вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | одно из |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Информационная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Содержание |
Определение
Биномиальное распределение — дискретное распределение вероятностей случайной величины принимающей целочисленные значения
с вероятностями:
Данное распределение характеризуется двумя параметрами: целым числом называемым числом испытаний, и вещественным числом
называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из
независимых испытаний, в каждом из которых может произойти "успех" с вероятностью
то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы
независимых слагаемых, имеющих распределение Бернулли.
Основные свойства
- Математическое ожидание:
- Дисперсия:
- Асимметрия:
при
распределение симметрично относительно центра
Асимптотические приближения при больших 
Если значения велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно.
В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).
Приближение Пуассона
Приближение распределением Пуассона применяется в ситуациях, когда значения большие, а значения
близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром
Строгая формулировка: если и
таким образом, что
то
Более того, справедлива следующая оценка. Пусть — случайная величина, имеющая распределение Пуассона с параметром
Тогда для произвольного множества
справедливо неравенство:
Доказательство и обзор более точных результатов, касающихся точности данного приближения, можно найти в [1, гл. III, §12].
Нормальное приближение
Приближение нормальным распределением используется в ситуациях, когда а
фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применение которой основано на представлении
в виде суммы
слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной величины
где
близко к стандартному нормальному.
Локальная теорема Муавра-Лапласа
Данная теорема используется для приближенного вычисления вероятностей отдельных значений биномиального распределения. Она утверждает [1, гл. I, §6], что равномерно по всем значениям таким что
имеет место
где — плотность стандартного нормального распределения.
Интегральная теорема Муавра-Лапласа
На практике необходимость оценки вероятностей отдельных значений, которую дает локальная теорема Муавра-Лапласа, возникает нечасто. Гораздо более важно оценивать вероятности событий, включающих в себя множество значений. Для этого используется интегральная теорема, которую можно сформулировать в следующем виде [1, гл. I, §6]:
при
где случайная величина имеет стандартное нормальное распределение
и аппроксимирующая вероятность определяется по формуле
где — функция распределения стандартного нормального закона:
Есть ряд результатов, позволяющих оценить скорость сходимости. В [1, гл. I, §6] приводится следующий результат, являющийся частным случаем теоремы Берри-Эссеена:
где — функция распределения случайной величины
На практике решение о том, насколько следует доверять нормальному приближению, принимают исходя из величины
Чем она больше, тем меньше будет погрешность приближения.
Заметим, что асимптотический результат не изменится, если заменить строгие неравенства на нестрогие и наоборот. Предельная вероятность от такой замены также не поменяется, так как нормальное распределение абсолютно непрерывно и вероятность принять любое конкретное значение для него равна нулю. Однако исходная вероятность от такой замены может измениться, что вносит в формулу некоторую неоднозначность. Для больших значений изменение будет невелико, однако для небольших
это может внести дополнительную погрешность.
Для устранения этой неоднозначности, а также повышения точности приближения рекомендуется задавать интересующие события в виде интервалов с полуцелыми границами. При этом приближение получается точнее. Это связано с тем интуитивно понятным соображением, что аппроксимация кусочно-постоянной функции (функции распределения биномиального закона) с помощью непрерывной функции дает более точные приближения между точками разрыва, чем в этих точках.
Пример
Пусть
Оценим вероятность того, что число успехов будет отличаться от наиболее вероятного значения
не более чем на
. Заметим, что значение
очень мало, поэтому применение нормального приближения здесь довольно ненадежно.
Точная вероятность рассматриваемого события равна
Применим нормальное приближение с той расстановкой неравенств, которая дана выше (снизу строгое, сверху нестрогое):
Ошибка приближения равна .
Теперь построим приближение, используя интервал с концами в полуцелых точках:
Ошибка приближения равна — примерно в 5 раз меньше, чем в предыдущем подходе.
Литература
1. Ширяев А.Н. Вероятность. — М.: МЦНМО, 2004.
Ссылки
- Биномиальное распределение (Википедия)
- Binomial distribution (Wikipedia)

