Интерполяция каноническим полиномом
Материал из MachineLearning.
(→Полином в каноническом виде) |
|||
| (15 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | + | {{TOCright}} | |
| + | '''Интерполяция''' — приближение одной функции другой функцией. | ||
| - | + | С самого начала хотелось бы заметить, что мы занимаемся интерполяцией '''функций''', а не узлов. Разумеется, интерполяция будет проводиться в конечном числе точек, но выбирать их мы будем сами. | |
| - | + | В настоящем исследовании будет изучена проблема интерполяции [http://ru.wikipedia.org/wiki/Функция_(математика) функции] одной переменной [http://ru.wikipedia.org/wiki/Многочлен полиномом] каноническим полиномом, будет рассмотрен вопрос точности приближения, и как, варьируя узлы, через которые пройдёт полином, достигнуть максимальной точности интерполяции. | |
| - | + | ||
| - | + | ||
=== Полином в каноническом виде === | === Полином в каноническом виде === | ||
| + | Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом P<sub>n</sub>(x). | ||
| + | Справедлива следующая '''Теорема (Вейерштрасса):''' ''Для любого <tex>\eps</tex>>0 существует полином P<sub>n</sub>(x) степени <tex>n=n(\eps)</tex>, такой, что <tex>max_{x \in [a,b]}|f(x)-P_n(x)|<\eps</tex>'' | ||
| - | В качестве аппроксимирующей функции | + | В качестве аппроксимирующей функции выберем полином степени ''n'' в каноническом виде: |
| - | <tex> | + | <tex>f(x)=P_n(x)=c_0+c_1x+c_2x^2+ \ldots + c_nx^n </tex> |
| - | Коэффициенты полинома <tex>c_i</tex> | + | Коэффициенты полинома <tex>c_i</tex> определим из условий Лагранжа <tex>P_n(x_i)=y_i</tex>, <tex>i=1, \ldots, n</tex>, что с учётом предыдущего выражения даёт [http://ru.wikipedia.org/wiki/Система_линейных_алгебраических_уравнений систему линейных алгебраических уравнений] с ''n''+1 неизвестными: |
<tex> | <tex> | ||
| Строка 26: | Строка 27: | ||
Обозначим систему таких уравнений символом (*) и перепишем её следующим образом: | Обозначим систему таких уравнений символом (*) и перепишем её следующим образом: | ||
| - | <tex> \sum_{p=0}^n c_i^p = y_i, \quad i=1, \ldots, n </tex> | + | <tex>\sum_{p=0}^n c_i^p = y_i, \quad i=1, \ldots, n</tex> |
| - | или в матричной форме: <tex>\mathbf{Ac}=\mathbf{y},</tex> где <tex>\mathbf{c}</tex> - | + | или в [http://ru.wikipedia.org/wiki/Матрица_(математика) матричной] форме: <tex>\mathbf{Ac}=\mathbf{y},</tex> где <tex>\mathbf{c}</tex> - [http://ru.wikipedia.org/wiki/Вектор вектор-столбец], содержащий неизвестные коэффициенты <tex>c_i</tex>, <tex>\mathbf{y}</tex> - вектор-столбец, составленный из табличных значений функции <tex>y_i</tex>, а матрица <tex>\mathbf{A}</tex> имеет вид: |
<tex> \mathbf{A} = | <tex> \mathbf{A} = | ||
| Строка 39: | Строка 40: | ||
</tex> | </tex> | ||
| - | Система линейных алгебраических уравнений (*) относительно неизвестных <tex>c_i</tex> | + | Система линейных алгебраических уравнений (*) относительно неизвестных <tex>c_i</tex> иметь единственное решение, если [http://ru.wikipedia.org/wiki/Определитель определитель] матрицы <tex>\mathbf{A}</tex> отличен от нуля. |
Определитель матрицы <tex>\mathbf{A}</tex> называют определителем Вандермонда, его можно вычислить по следующей формуле: | Определитель матрицы <tex>\mathbf{A}</tex> называют определителем Вандермонда, его можно вычислить по следующей формуле: | ||
| Строка 45: | Строка 46: | ||
<tex>\mathbf{detA} = \prod_{i,j=0 \\ i \neq j }^n (x_i - x_j) \neq 0 </tex> | <tex>\mathbf{detA} = \prod_{i,j=0 \\ i \neq j }^n (x_i - x_j) \neq 0 </tex> | ||
| - | {{ | + | Число узлов интерполяционного полинома должно быть на единицу больше его степени. Это понятно из интуитивных соображений: через 2 точки можно провести единственную прямую, через 3 - единственную параболу и т.д. Но полином может получиться и меньшей степени. Т.е. если 3 точки лежат на одной прямой, то через них пройдёт единственный полином первой степени (но это ничему не противоречит: просто коэффициент при старшей степени равен нулю). |
| + | |||
| + | При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции, что можно показать на следующем графике | ||
| + | |||
| + | [[Изображение:Report1-fig1.gif|Зависимость числа обусловленности матрицы от количества узлов интерполяции]] | ||
| + | |||
| + | Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, [[Интерполяция полиномами Лагранжа и Ньютона | интерполяция полиномами Лагранжа]]). При этом важно понимать, что при теоретическом применении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином. | ||
| + | |||
| + | Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры. | ||
| + | |||
| + | === Способ вычисления полинома в точке === | ||
| + | Чтобы изобразить графически аппроксимирующий полином, необходимо вычислить его значение в ряде точек. Это можно сделать следующими способами. | ||
| + | |||
| + | '''Первый способ.''' Можно посчитать значение a<sub>1</sub>x и сложить с a<sub>0</sub>. Далее найти a<sub>2</sub>x<sup>2</sup>, сложить с полученным результатом, и так далее. Таким образом, на j-ом шаге вычисляется значение a<sub>j</sub>x<sup>j</sup> и складывается с уже вычисленной суммой <tex>a_0 + a_1x + \ldots + a_{j-1}x^{j-1}</tex>. | ||
| + | |||
| + | Вычисление значения a<sub>j</sub>x<sup>j</sup> требует j операций умножения. Т.е. для подсчёта многочлена в заданной точке требуется (1 + 2 + ... + n) = n(n+1)/2 операций умножения и n операций сложения. Всего операций в данном случае: Op<sub>1</sub> = n(n+1)/2 + n. | ||
| + | |||
| + | '''Второй способ.''' Полином можно также легко вычислить с помощью так называемой '''схемы Горнера:''' <tex>P_n(x) = (\ldots ((a_nx + a_{n-1})x + a_{n-2})x + \ldots)x + a_0</tex> | ||
| + | |||
| + | Для вычисления значения во внутренних скобках a<sub>n</sub>x + a<sub>n-1</sub> требуется одна операция умножения и одна операция сложения. Для вычисления значения в следующих скобках (a<sub>n</sub>x + a<sub>n-1</sub>)x + a<sub>n-2</sub> требуется опять одна операция умножения и одна операция сложения, т.к. a<sub>n</sub>x + a<sub>n-1</sub> уже вычислено, и т.д. | ||
| + | |||
| + | Тогда в этом способе вычисление P<sub>n</sub>(x) потребует n операций умножения и n операций сложения, т.е. сложность вычислений Op<sub>2</sub> = n+n = 2n. | ||
| + | Ясно, что Op<sub>2</sub> << Op<sub>1</sub>. | ||
| + | |||
| + | == Анализ метода == | ||
| + | === Сложность вычислений === | ||
| + | Оценка сложности интерполирования функции складывается из количества операций для решения [[Система линейных алгебраических уравнений|системы линейных алгебраических уравнений]] (СЛАУ) и нахождения значения полинома в точке. | ||
| + | |||
| + | Сложность решения СЛАУ, например, [http://ru.wikipedia.org/wiki/Метод_Гаусса методом Гаусса] для матрицы размера ''n''x''n'': 2''n''<sup>3</sup>/3, т.е. O(''n''<sup>3</sup>). | ||
| + | |||
| + | Для нахождения полинома в заданной точке требуется ''n'' умножений и ''n'' сложений. В результате сложность метода: O(''n''<sup>3</sup>). | ||
| + | |||
| + | === Погрешность интерполяции === | ||
| + | Предположим, что на отрезке интерполирования [''a,b''] функция ''f(x)'' ''n'' раз непрерывно-дифференцируема. Погрешность интерполяции складывается из погрешности самого метода и [[Ошибки вычислений | ошибок округления.]] | ||
| + | |||
| + | Ошибка приближения функции ''f(x)'' интерполяционным полиномом ''n''-ой степени ''P<sub>n</sub>(x)'' в точке ''x'' определяется разностью: ''R<sub>n</sub>(x) = f(x) - P<sub>n</sub>(x).'' | ||
| + | |||
| + | Погрешность ''R<sub>n</sub>(x)'' определяется следующим соотношением: | ||
| + | <br><tex>R_n(x) = \frac{f^{n+1}(\xi)}{(n+1)!}\omega_n(x)</tex> | ||
| + | |||
| + | Здесь <tex>f^{n+1}(\xi)</tex> - производная ''(n+1)''-го порядка функции ''f(x)'' в некоторой точке <tex>\xi \in [a,b],</tex> а функция <tex>\omega_n(x)</tex> определяется как | ||
| + | <br><tex>\omega_n(x)=(x-x_0)(x-x_1)\ldots (x-x_n).</tex> | ||
| + | |||
| + | Если максимальное значение производной ''f<sup>n+1</sup>(x)'' равно <tex>M_{n+1} = \sup_{x \in [x_0, x_n]} \left| f^{n+1}(x) \right| ,</tex> то для погрешности интерполяции следует оценка: <tex>\left| R_n(x) \right| = \frac{M_{n+1}}{(n+1)!}\omega_n(x).</tex> | ||
| + | |||
| + | При реализации данного метода на ЭВМ ошибкой интерполяции ''E<sub>n</sub>(x)'' будем считать максимальное уклонение полинома от исходной функции на выбранном промежутке: <tex>E_n(x) = \max_{x \in [a, b]} \left| f(x) - P_n(x) \right| .</tex> | ||
| + | |||
| + | === Выбор узлов интерполяции === | ||
| + | Ясно, что от выбора узлов интерполируемой функции напрямую зависит, насколько точно многочлен будет являться её приближением. | ||
| + | |||
| + | Введём следующее '''определение''': полиномом Чебышева называется многочлен вида | ||
| + | <br><center>T<sub>k</sub>(x) = cos(k arccos x), |x|≤1.</center> | ||
| + | |||
| + | Известно (см. ссылки литературы), что если узлы интерполяции ''x<sub>0</sub>, x<sub>1</sub>,...,x<sub>n</sub>'' являются корнями полинома Чебышева степени ''n+1'', то величина <tex>\max_{x \in [a,b]} \left| \omega_{n+1}(x) \right|</tex> принимает наименьшее возможное значение по сравнению с любым другим выбором набора узлов интерполяции. | ||
| + | |||
| + | Очевидно, что в случае ''k'' = 1 функция ''T<sub>1</sub>(x)'', действительно, является полиномом первой степени, поскольку T<sub>1</sub>(x) = cos(arccos x) = x. | ||
| + | |||
| + | В случае ''k'' = 2 ''T<sub>2</sub>(x)'' тоже полином второй степени. Это нетрудно проверить. Воспользуемся известным тригонометрическим тождеством: cos2<i>θ</i> = 2cos²<i>θ</i> - 1, положив ''θ'' = arccos ''x''. | ||
| + | |||
| + | Тогда получим следующее соотношение: <i>T<sub>2</sub>(x)</i> = 2x² - 1. | ||
| + | |||
| + | С помощью тригонометрического тождества cos(<i>k</i> + 1)<i>θ</i> = 2cos<i>θ</i>cos<i>kθ</i> - cos(<i>k</i> - 1) легко показать, что для полиномов Чебышева справедливо реккурентное соотношение: | ||
| + | <p align="center"><i>T<sub>k+1</sub>(x) = 2xT<sub>k</sub>(x) - T<sub>k-1</sub>(x)</i></p> | ||
| + | |||
| + | При помощи данного соотношения можно получить формулы для полиномов Чебышева любой степени. | ||
| + | |||
| + | Корни полинома Чебышева легко находятя из уравнения: ''T<sub>k</sub>(x)'' = cos(''k'' arccos ''x'') = 0. Получаем, что уравнение имеет ''k'' различных корней, расположенных на отрезке [-1,1]: <tex>x_m = \cos \frac{2m+1}{2k}\pi, \, m = 0,1, \cdots, k-1,</tex> которые и следует выбирать в качестве узлов интерполирования. | ||
| + | |||
| + | Нетрудно видеть, что корни на [-1,1] расположены симметрично и неравномерно - чем ближе к краям отрезка, тем корни расположены плотнее. Максимальное значение модуля полинома Чебышева равно 1 и достигается в точках <tex>\cos \frac{m}{k}\pi.</tex> | ||
| + | |||
| + | Если положить <tex>\omega_k(x) = \frac1{2^{k-1}}T_k(x),</tex> то для того, чтобы коэффициент при старшей степени полинома <i>ω<sub>k</sub>(x)</i> был равен 1, <tex>\max_{x \in [-1,1]}\omega_k(x) = \frac1{2^{k-1}}.</tex> | ||
| + | |||
| + | Известно, что для любого полинома ''p<sub>k</sub>(x)'' степени ''k'' с коэффициентом, равным единице при старшей производной верно неравенство <tex>\max_{x \in [-1,1]}p_k(x) \geq \frac1{2^{k-1}},</tex> т.е. полиномы Чебышева являются полиномами, наименее уклоняющимися от нуля. | ||
| + | |||
| + | == Вычислительный эксперимент == | ||
| + | |||
| + | Для реализации поставленной задачи была написана [[Media:Deryabin-prak1.zip| программа]] на языке С++, которая по заданной функции приближает её каноническим полиномом. Разумеется, необходимо указать узлы, через которые полином пройдёт, и значения функции в этих узлах. | ||
| + | |||
| + | Далее строится СЛАУ, которая решается методом Гаусса. На выходе получаем коэффициенты для полинома и ошибку аппроксимации. | ||
| + | |||
| + | Как было показано выше, и в чём мы убедимся в дальнейшем, от выбора узлов зависит точность, с которой полином будет приближать функцию. | ||
| + | |||
| + | === Пример: Интерполяция синуса === | ||
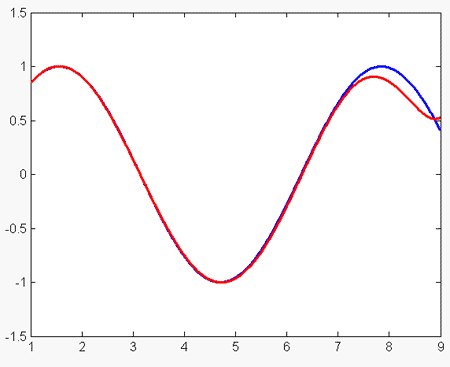
| + | Попробуем интерполировать функцию y = sin(x) на отрезке [1, 8.5]. Выберем узлы интерполяции: {1.1, 2, 4.7, 7.5, 8.5} | ||
| + | |||
| + | Полученный в результате интерполяции полином отображён на рисунке (синим цветом показан график ''y'' = sin(''x''), красным – интерполяционного полинома) | ||
| + | |||
| + | [[Изображение:Report1-fig2.gif]] | ||
| + | |||
| + | Ошибка интерполяции в этом случае: '''0.1534''' | ||
| + | |||
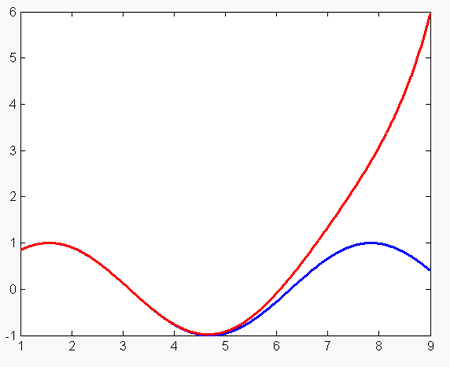
| + | Давайте посмотрим, что произойдёт, если выбрать равномерно стоящие узлы {2, 3.5 5, 6.5, 8} для той же функции на том же отрезке. | ||
| + | |||
| + | На отрезке [3, 6] приближение, бесспорно, стало лучше. Однако разброс на краях очень большой. Ошибка интерполяции: '''2.3466'''. | ||
| + | |||
| + | [[Изображение:Report1-fig3.gif]] | ||
| + | |||
| + | Наконец, выберем узлы интерполяции в соответствии с Чебышевским алгоритмом. Получим их по следующей формуле (просто сделаем замену переменной): | ||
| + | <tex>x_m = \frac{a+b}{2} + \frac{b-a}{2}\cos \frac{\pi(2m-1)}{2n}, \, m=1,2, \cdots, n.</tex> | ||
| + | <tex>y_m = y(x_m)</tex> | ||
| + | |||
| + | В нашем случае [''a,b''] - отрезок [1, 8.5], ''y'' = cos''x'', ''n+1'' - количество узлов. | ||
| + | |||
| + | Остаётся открытым вопрос, какое количество узлов выбрать. | ||
| + | *При значении ''n'' меньше '''3''' ошибка аппроксимации получается более '''10.6626.''' | ||
| + | *При ''n'' = '''4''': приближение лучше (ошибка равна '''1.0111'''), | ||
| + | *при ''n'' = '''5''': ошибка аппроксимации '''0.2797''' | ||
| + | |||
| + | График функций при ''n'' = 4 выглядит следующим образом: | ||
| + | |||
| + | [[Изображение:Report1-fig4-4pts.gif]] | ||
| + | |||
| + | Продолжим исследования. | ||
| + | *''n'' = '''6''': ошибка аппроксимации '''1.0233.''' | ||
| + | |||
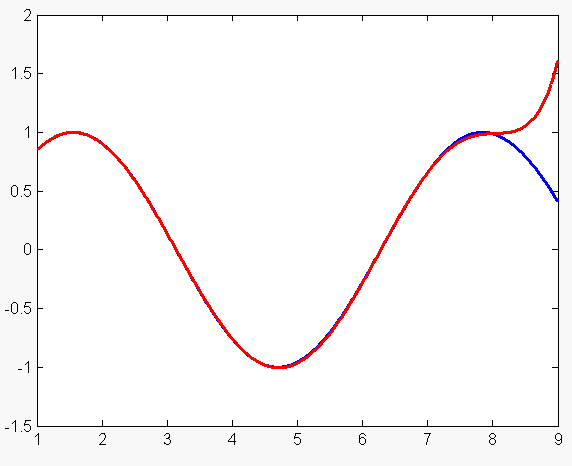
| + | При ''n'' = '''7''' ошибка аппроксимации принимает наименьшее из полученных ранее значений (для данного промежутка): '''0.0181'''. График синуса (обозначен синим цветом) и аппроксимационного полинома (обозначен красным цветом) представлены на следующем графике: | ||
| + | |||
| + | [[Изображение:Report1-fig4-7pts.gif]] | ||
| + | |||
| + | Что интересно, если при этом же количестве узлов выбирать их на отрезке [1, 8], то ошибка аппроксимации становится ещё меньше : '''0.0124'''. График в этом случае выглядит так: | ||
| + | |||
| + | [[Изображение:Report1-fig4-7-2pts.gif]] | ||
| + | |||
| + | При выборе большего количества узлов ситуация ухудшается: мы стараемся слишком точно приблизить исходную функцию: | ||
| + | |||
| + | [[Изображение:Report1-fig4-8pts.gif]] | ||
| + | |||
| + | Ошибка аппроксимации будет только расти с увеличением числа узлов. | ||
| + | |||
| + | Как видим, наилучшее приближение получается при выборе узлов по методу Чебышева. Однако рекомендаций, какое количество узлов является оптимальным, нет - это определяется только экспериментальным путём. | ||
| + | |||
| + | == Рекомендации программисту == | ||
| + | Программа написана на языке C++ с использованием библиотеки линейной алгебры UBlas, которая является частью собрания библиотек [http://boost.org/ Boost.] Скачать исходный текст программы можно [[Media:Deryabin-prak1.zip| здесь [2.55Кб].]] | ||
| + | |||
| + | === Предварительные настойки === | ||
| + | Чтобы воспользоваться программой, необходимо сделать следующее: | ||
| + | 1. Определиться с функцией, которую вы собираетесь интерполировать | ||
| + | 2. Создать текстовый файл (например, '''vec.txt'''), в первой строчке которого через пробел размещены узлы интерполяции, а во второй – значения выбранной функции в этих узлах. | ||
| + | |||
| + | Например, функция y = sin(x): | ||
| + | |||
| + | <pre> | ||
| + | 0.74 2 -3.5 | ||
| + | 0.6743 0.9093 0.351 | ||
| + | </pre> | ||
| + | |||
| + | 3. В .cpp файле программы в функцию double f(double x) вместо строки return прописать возвращаемое исходной функцией значение. Например, для функции y = sin(x): | ||
| + | <pre> | ||
| + | return sin(x); | ||
| + | </pre> | ||
| + | 4. В функции '''int main()''' исходного кода присвоить переменной '''char* flname''' путь к входному файлу с данными. В нашем случае '''char* flname = "vec.txt";''' | ||
| + | |||
| + | === Использование программы === | ||
| + | В программе реализованы следующие основные функции: | ||
| + | * '''double f(double x)''', описание которой было дано выше | ||
| + | * '''int load(char *filename, vector<double> &x, vector<double> &y)''' - загрузка узлов интерполяции в переменную '''x''' и значения функции в этих узлах в переменную '''y''' текстового файла '''filename'''. В случае удачной загрузки данных из файла функция возвращает '''0'''. | ||
| + | * '''void matrix2diag(matrix<double> &A, vector<double> &y)''' - приводит матрицу '''A''' к треугольному виду. '''y''' - столбец правой части (также изменяется вместе с матрицей '''A'''). | ||
| + | * '''void SolveSystem(matrix<double> &A, vector<double> &y, vector<double> &coef)''' - решить СЛАУ ('''A''' - треугольная матрица, '''y''' - столбец правой части, '''coef''' - в этот вектор заносится решение СЛАУ) | ||
| + | * '''double errapprox(vector<double> coef, double a, double b, double h)''' – возвращает ошибку аппроксимации полиномом исходной функции. | ||
| + | |||
| + | На вход функции подаются следующие параметры: | ||
| + | |||
| + | ** '''vector coef''' – вектор коэффициентов интерполяционного полинома, который получается в ходе решения СЛАУ | ||
| + | ** '''double a, double b''' – границы промежутка интерполяции [a, b] | ||
| + | ** '''double h''' – шаг, с которым «пробегаем» промежуток [a, b] | ||
| + | |||
| + | * '''int outpolyn(char** filename, vector<double> coef)''' – сохраняет коэффициенты полинома '''coef''' в файл '''filename'''. В случае удачного сохранения функция возвращает '0'. | ||
| + | |||
| + | После запуска программы на экране появляются коэффициенты интерполяционного полинома и ошибка аппроксимации. | ||
| + | |||
| + | == Вывод == | ||
| + | Был исследован и программно реализован метод интерполяции функции каноническим полиномом. В ходе исследований установлено, что ошибка интерполяции получается как из-за ошибок компьютерных вычислений, так и из-за ошибок метода. | ||
| + | |||
| + | Также замечено, что от выбора узлов интерполяции напрямую зависит качество интерполяции. Минимальная ошибка интерполяции достигается при выборе «чебышевских» узлов. | ||
| + | |||
| + | == Прикреплённые файлы == | ||
| + | |||
| + | [[Media:Deryabin-prak1.zip| Программная реализация на языке С++ (исходный текст) [2.55Кб]]] | ||
| + | |||
| + | == Литература == | ||
| + | |||
| + | * ''Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков.'' Численные методы. Изд-во "Лаборатория базовых знаний". Москва. 2003. | ||
| + | * ''И.С. Березин, Н.П. Жидков.'' Методы вычислений. Изд. ФизМатЛит. Москва. 1962. | ||
| + | * ''Дж. Форсайт, М.Мальком, К. Моулер.'' Машинные методы математических вычислений. Изд-во "Мир". Москва. 1980. | ||
| + | |||
| + | == Смотри также == | ||
| + | * [[Интерполяция функций двух переменных, проблема выбора узлов | Проблема выбора узлов для интерполяции]] | ||
| + | * [[Ошибки вычислений]] | ||
| + | * [[Метод наименьших квадратов]] | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%82%D0%B5%D1%80%D0%BF%D0%BE%D0%BB%D1%8F%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D1%87%D0%BB%D0%B5%D0%BD_%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%D0%B0 Интерполяционный многочлен Лагранжа] | ||
| + | * [[Практикум ММП ВМК, 4й курс, осень 2008]] | ||
| + | |||
| + | == Ссылки == | ||
| + | * [http://boost.org/ Собрание библиотек Boost] | ||
| + | |||
| + | [[Категория:Учебные задачи]] | ||
Текущая версия
|
Интерполяция — приближение одной функции другой функцией.
С самого начала хотелось бы заметить, что мы занимаемся интерполяцией функций, а не узлов. Разумеется, интерполяция будет проводиться в конечном числе точек, но выбирать их мы будем сами.
В настоящем исследовании будет изучена проблема интерполяции функции одной переменной полиномом каноническим полиномом, будет рассмотрен вопрос точности приближения, и как, варьируя узлы, через которые пройдёт полином, достигнуть максимальной точности интерполяции.
Полином в каноническом виде
Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом Pn(x).
Справедлива следующая Теорема (Вейерштрасса): Для любого >0 существует полином Pn(x) степени
, такой, что
В качестве аппроксимирующей функции выберем полином степени n в каноническом виде:
Коэффициенты полинома определим из условий Лагранжа
,
, что с учётом предыдущего выражения даёт систему линейных алгебраических уравнений с n+1 неизвестными:
Обозначим систему таких уравнений символом (*) и перепишем её следующим образом:
или в матричной форме: где
- вектор-столбец, содержащий неизвестные коэффициенты
,
- вектор-столбец, составленный из табличных значений функции
, а матрица
имеет вид:
Система линейных алгебраических уравнений (*) относительно неизвестных иметь единственное решение, если определитель матрицы
отличен от нуля.
Определитель матрицы называют определителем Вандермонда, его можно вычислить по следующей формуле:
Число узлов интерполяционного полинома должно быть на единицу больше его степени. Это понятно из интуитивных соображений: через 2 точки можно провести единственную прямую, через 3 - единственную параболу и т.д. Но полином может получиться и меньшей степени. Т.е. если 3 точки лежат на одной прямой, то через них пройдёт единственный полином первой степени (но это ничему не противоречит: просто коэффициент при старшей степени равен нулю).
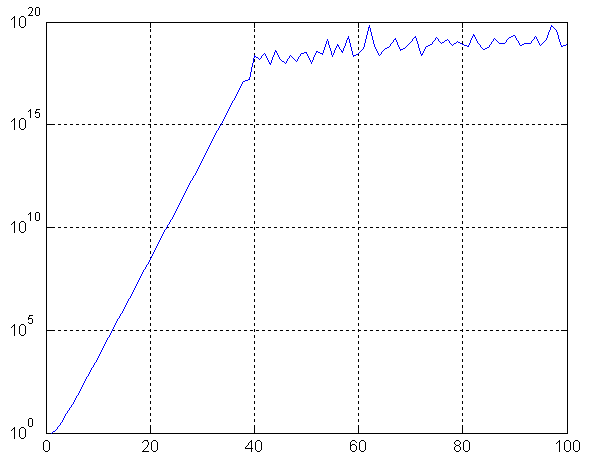
При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции, что можно показать на следующем графике
Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, интерполяция полиномами Лагранжа). При этом важно понимать, что при теоретическом применении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином.
Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры.
Способ вычисления полинома в точке
Чтобы изобразить графически аппроксимирующий полином, необходимо вычислить его значение в ряде точек. Это можно сделать следующими способами.
Первый способ. Можно посчитать значение a1x и сложить с a0. Далее найти a2x2, сложить с полученным результатом, и так далее. Таким образом, на j-ом шаге вычисляется значение ajxj и складывается с уже вычисленной суммой .
Вычисление значения ajxj требует j операций умножения. Т.е. для подсчёта многочлена в заданной точке требуется (1 + 2 + ... + n) = n(n+1)/2 операций умножения и n операций сложения. Всего операций в данном случае: Op1 = n(n+1)/2 + n.
Второй способ. Полином можно также легко вычислить с помощью так называемой схемы Горнера:
Для вычисления значения во внутренних скобках anx + an-1 требуется одна операция умножения и одна операция сложения. Для вычисления значения в следующих скобках (anx + an-1)x + an-2 требуется опять одна операция умножения и одна операция сложения, т.к. anx + an-1 уже вычислено, и т.д.
Тогда в этом способе вычисление Pn(x) потребует n операций умножения и n операций сложения, т.е. сложность вычислений Op2 = n+n = 2n. Ясно, что Op2 << Op1.
Анализ метода
Сложность вычислений
Оценка сложности интерполирования функции складывается из количества операций для решения системы линейных алгебраических уравнений (СЛАУ) и нахождения значения полинома в точке.
Сложность решения СЛАУ, например, методом Гаусса для матрицы размера nxn: 2n3/3, т.е. O(n3).
Для нахождения полинома в заданной точке требуется n умножений и n сложений. В результате сложность метода: O(n3).
Погрешность интерполяции
Предположим, что на отрезке интерполирования [a,b] функция f(x) n раз непрерывно-дифференцируема. Погрешность интерполяции складывается из погрешности самого метода и ошибок округления.
Ошибка приближения функции f(x) интерполяционным полиномом n-ой степени Pn(x) в точке x определяется разностью: Rn(x) = f(x) - Pn(x).
Погрешность Rn(x) определяется следующим соотношением:
Здесь - производная (n+1)-го порядка функции f(x) в некоторой точке
а функция
определяется как
Если максимальное значение производной fn+1(x) равно то для погрешности интерполяции следует оценка:
При реализации данного метода на ЭВМ ошибкой интерполяции En(x) будем считать максимальное уклонение полинома от исходной функции на выбранном промежутке:
Выбор узлов интерполяции
Ясно, что от выбора узлов интерполируемой функции напрямую зависит, насколько точно многочлен будет являться её приближением.
Введём следующее определение: полиномом Чебышева называется многочлен вида
Известно (см. ссылки литературы), что если узлы интерполяции x0, x1,...,xn являются корнями полинома Чебышева степени n+1, то величина принимает наименьшее возможное значение по сравнению с любым другим выбором набора узлов интерполяции.
Очевидно, что в случае k = 1 функция T1(x), действительно, является полиномом первой степени, поскольку T1(x) = cos(arccos x) = x.
В случае k = 2 T2(x) тоже полином второй степени. Это нетрудно проверить. Воспользуемся известным тригонометрическим тождеством: cos2θ = 2cos²θ - 1, положив θ = arccos x.
Тогда получим следующее соотношение: T2(x) = 2x² - 1.
С помощью тригонометрического тождества cos(k + 1)θ = 2cosθcoskθ - cos(k - 1) легко показать, что для полиномов Чебышева справедливо реккурентное соотношение:
Tk+1(x) = 2xTk(x) - Tk-1(x)
При помощи данного соотношения можно получить формулы для полиномов Чебышева любой степени.
Корни полинома Чебышева легко находятя из уравнения: Tk(x) = cos(k arccos x) = 0. Получаем, что уравнение имеет k различных корней, расположенных на отрезке [-1,1]: которые и следует выбирать в качестве узлов интерполирования.
Нетрудно видеть, что корни на [-1,1] расположены симметрично и неравномерно - чем ближе к краям отрезка, тем корни расположены плотнее. Максимальное значение модуля полинома Чебышева равно 1 и достигается в точках
Если положить то для того, чтобы коэффициент при старшей степени полинома ωk(x) был равен 1,
Известно, что для любого полинома pk(x) степени k с коэффициентом, равным единице при старшей производной верно неравенство т.е. полиномы Чебышева являются полиномами, наименее уклоняющимися от нуля.
Вычислительный эксперимент
Для реализации поставленной задачи была написана программа на языке С++, которая по заданной функции приближает её каноническим полиномом. Разумеется, необходимо указать узлы, через которые полином пройдёт, и значения функции в этих узлах.
Далее строится СЛАУ, которая решается методом Гаусса. На выходе получаем коэффициенты для полинома и ошибку аппроксимации.
Как было показано выше, и в чём мы убедимся в дальнейшем, от выбора узлов зависит точность, с которой полином будет приближать функцию.
Пример: Интерполяция синуса
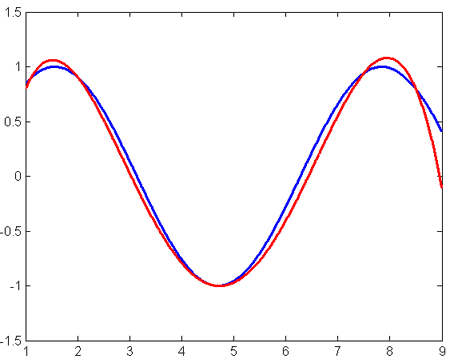
Попробуем интерполировать функцию y = sin(x) на отрезке [1, 8.5]. Выберем узлы интерполяции: {1.1, 2, 4.7, 7.5, 8.5}
Полученный в результате интерполяции полином отображён на рисунке (синим цветом показан график y = sin(x), красным – интерполяционного полинома)
Ошибка интерполяции в этом случае: 0.1534
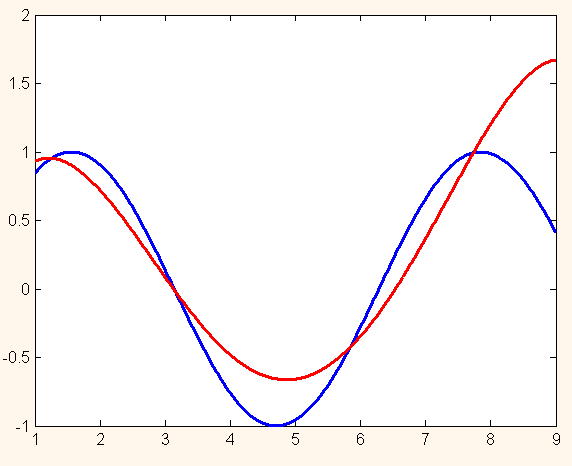
Давайте посмотрим, что произойдёт, если выбрать равномерно стоящие узлы {2, 3.5 5, 6.5, 8} для той же функции на том же отрезке.
На отрезке [3, 6] приближение, бесспорно, стало лучше. Однако разброс на краях очень большой. Ошибка интерполяции: 2.3466.
Наконец, выберем узлы интерполяции в соответствии с Чебышевским алгоритмом. Получим их по следующей формуле (просто сделаем замену переменной):
В нашем случае [a,b] - отрезок [1, 8.5], y = cosx, n+1 - количество узлов.
Остаётся открытым вопрос, какое количество узлов выбрать.
- При значении n меньше 3 ошибка аппроксимации получается более 10.6626.
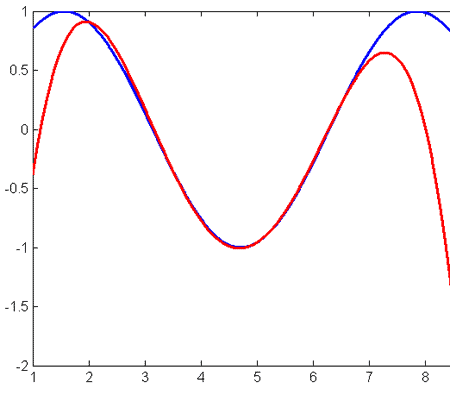
- При n = 4: приближение лучше (ошибка равна 1.0111),
- при n = 5: ошибка аппроксимации 0.2797
График функций при n = 4 выглядит следующим образом:
Продолжим исследования.
- n = 6: ошибка аппроксимации 1.0233.
При n = 7 ошибка аппроксимации принимает наименьшее из полученных ранее значений (для данного промежутка): 0.0181. График синуса (обозначен синим цветом) и аппроксимационного полинома (обозначен красным цветом) представлены на следующем графике:
Что интересно, если при этом же количестве узлов выбирать их на отрезке [1, 8], то ошибка аппроксимации становится ещё меньше : 0.0124. График в этом случае выглядит так:
При выборе большего количества узлов ситуация ухудшается: мы стараемся слишком точно приблизить исходную функцию:
Ошибка аппроксимации будет только расти с увеличением числа узлов.
Как видим, наилучшее приближение получается при выборе узлов по методу Чебышева. Однако рекомендаций, какое количество узлов является оптимальным, нет - это определяется только экспериментальным путём.
Рекомендации программисту
Программа написана на языке C++ с использованием библиотеки линейной алгебры UBlas, которая является частью собрания библиотек Boost. Скачать исходный текст программы можно здесь [2.55Кб].
Предварительные настойки
Чтобы воспользоваться программой, необходимо сделать следующее: 1. Определиться с функцией, которую вы собираетесь интерполировать 2. Создать текстовый файл (например, vec.txt), в первой строчке которого через пробел размещены узлы интерполяции, а во второй – значения выбранной функции в этих узлах.
Например, функция y = sin(x):
0.74 2 -3.5 0.6743 0.9093 0.351
3. В .cpp файле программы в функцию double f(double x) вместо строки return прописать возвращаемое исходной функцией значение. Например, для функции y = sin(x):
return sin(x);
4. В функции int main() исходного кода присвоить переменной char* flname путь к входному файлу с данными. В нашем случае char* flname = "vec.txt";
Использование программы
В программе реализованы следующие основные функции:
- double f(double x), описание которой было дано выше
- int load(char *filename, vector<double> &x, vector<double> &y) - загрузка узлов интерполяции в переменную x и значения функции в этих узлах в переменную y текстового файла filename. В случае удачной загрузки данных из файла функция возвращает 0.
- void matrix2diag(matrix<double> &A, vector<double> &y) - приводит матрицу A к треугольному виду. y - столбец правой части (также изменяется вместе с матрицей A).
- void SolveSystem(matrix<double> &A, vector<double> &y, vector<double> &coef) - решить СЛАУ (A - треугольная матрица, y - столбец правой части, coef - в этот вектор заносится решение СЛАУ)
- double errapprox(vector<double> coef, double a, double b, double h) – возвращает ошибку аппроксимации полиномом исходной функции.
На вход функции подаются следующие параметры:
- vector coef – вектор коэффициентов интерполяционного полинома, который получается в ходе решения СЛАУ
- double a, double b – границы промежутка интерполяции [a, b]
- double h – шаг, с которым «пробегаем» промежуток [a, b]
- int outpolyn(char** filename, vector<double> coef) – сохраняет коэффициенты полинома coef в файл filename. В случае удачного сохранения функция возвращает '0'.
После запуска программы на экране появляются коэффициенты интерполяционного полинома и ошибка аппроксимации.
Вывод
Был исследован и программно реализован метод интерполяции функции каноническим полиномом. В ходе исследований установлено, что ошибка интерполяции получается как из-за ошибок компьютерных вычислений, так и из-за ошибок метода.
Также замечено, что от выбора узлов интерполяции напрямую зависит качество интерполяции. Минимальная ошибка интерполяции достигается при выборе «чебышевских» узлов.
Прикреплённые файлы
Программная реализация на языке С++ (исходный текст) [2.55Кб]
Литература
- Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. Изд-во "Лаборатория базовых знаний". Москва. 2003.
- И.С. Березин, Н.П. Жидков. Методы вычислений. Изд. ФизМатЛит. Москва. 1962.
- Дж. Форсайт, М.Мальком, К. Моулер. Машинные методы математических вычислений. Изд-во "Мир". Москва. 1980.
Смотри также
- Проблема выбора узлов для интерполяции
- Ошибки вычислений
- Метод наименьших квадратов
- Интерполяционный многочлен Лагранжа
- Практикум ММП ВМК, 4й курс, осень 2008