Участник:Gukov/Песочница
Материал из MachineLearning.
(→Случай почти равных корней) |
(→Случай почти равных корней) |
||
| (7 промежуточных версий не показаны.) | |||
| Строка 45: | Строка 45: | ||
=== Случай почти равных корней === | === Случай почти равных корней === | ||
| - | [[Изображение:macon.png|thumb| | + | [[Изображение:macon.png|thumb|200px|Рисунок 1]] |
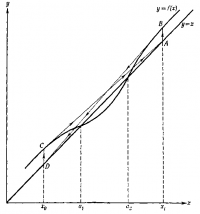
Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1 (масштаб сильно увеличен). Заметим, что производная <tex>f'(x)</tex> близка | Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1 (масштаб сильно увеличен). Заметим, что производная <tex>f'(x)</tex> близка | ||
к 1 при x, равном обоим значениям корней, <tex>a_1</tex> и <tex>a_2</tex>. Более того, на основании теоремы Лагранжа, можно утверждать, что <tex>f'(x) = 1</tex> где-то между <tex>a_1</tex> и <tex>a_2</tex>. | к 1 при x, равном обоим значениям корней, <tex>a_1</tex> и <tex>a_2</tex>. Более того, на основании теоремы Лагранжа, можно утверждать, что <tex>f'(x) = 1</tex> где-то между <tex>a_1</tex> и <tex>a_2</tex>. | ||
| Строка 53: | Строка 53: | ||
<tex>x_1</tex>. Касательная, проведенная через точку <tex>B</tex>, пересекает прямую в точке <tex>D</tex>, и в качестве следующего приближеня получается снова <tex>x_0</tex>. Итерационный процесс, таким образом, осциллирует между <tex>x_0</tex> и <tex>x_1</tex> | <tex>x_1</tex>. Касательная, проведенная через точку <tex>B</tex>, пересекает прямую в точке <tex>D</tex>, и в качестве следующего приближеня получается снова <tex>x_0</tex>. Итерационный процесс, таким образом, осциллирует между <tex>x_0</tex> и <tex>x_1</tex> | ||
до бесконечности, не сходясь ни к одному значению корня. Иначе говоря, не удается <i>отделить</i> эти два корня, потому что они расположены слишком близко. | до бесконечности, не сходясь ни к одному значению корня. Иначе говоря, не удается <i>отделить</i> эти два корня, потому что они расположены слишком близко. | ||
| + | |||
| + | Поэтому необходимо начальное приближение, достаточно близкое к искомому значению корня. Трудности возникают потому, что | ||
| + | вычисление знаменателя в формуле {{eqref|3}} включает в себя вычитание двух почти равных чисел, что приводит к понижению точности. | ||
== Изложение метода == | == Изложение метода == | ||
| - | === | + | === Поиск начального приближения === |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
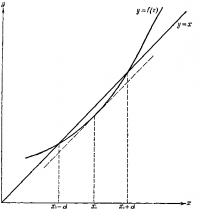
| - | то есть | + | [[Изображение:macon2.PNG|thumb|200px|Рисунок 2]] |
| + | Сначала находится значение x, при котором <tex>f'(x)=1</tex>, то есть решается уравнение | ||
| + | :<tex>x=x+f'(x)-1</tex> | ||
| + | Пусть решением этого уравнения будет некоторое <tex>x = x_0</tex>. Эта точка расположена между двумя корнями, <tex>a_1</tex> и <tex>a_2</tex>. Чтобы получить начальное приближение для решения уравнения, предположим, что <tex>x_0</tex> лежит посредине между | ||
| + | <tex>a_1</tex> и <tex>a_2</tex> (рисунок 2). Другими словами, мы предполагаем, что <tex>x_0 + d</tex> и <tex>x_0 - d</tex> являются корнями уравнения {{eqref|1.1}}. Разлагая <tex>f(x)</tex> в ряд Тейлора в окрестности точки <tex>x_0</tex> и принимая во внимание, что <tex>f'(x)=1</tex>, получаем | ||
| + | :<tex>f(x) = f(x_0) + (x - x_0) + \frac{1}{2} f''(x_0) (x - x_0)^2 + \ldots</tex> | ||
| - | + | Ограничим ряд тремя членами. Подставляя <tex>x + d</tex> вместо <tex>x</tex>, имеем | |
| + | :<tex>f(x_0+d) = f(x_0) + d + \frac{1}{2} f''(x_0)(d^2)</tex> | ||
| - | + | Но по условию | |
| - | :<tex> | + | :<tex>f(x_0+d) = x_0+d,</tex> |
| - | + | поэтому, решая эти уравнения относительно <tex>d</tex>, получаем | |
| + | :<tex>d=\sqrt{\frac{2(x_0 - f(x_0))}{f''(x_0)}}</tex> | ||
| - | + | Таким образом, процесс решения сводится к следующему. Если дано уравнение с почти равными корнями, то, определив приблизительное | |
| + | местонахождение этих корней, необходиом решить уравнение | ||
| + | :<tex>x = x + f'(x) - 1</tex> | ||
| - | + | и определить значение <tex>x_0</tex>. Для решения этого уравнения можно применить, например, метод Ньютона-Рафсона. | |
| - | <tex> | + | Найдя значение <tex>x_0</tex>, можно определить значение <tex>d</tex>. И, наконец, значения <tex>x_0-d</tex> и <tex>x_0+d</tex> |
| - | + | используются в качестве начальных приближений для определения соответственно <tex>a_1</tex> и <tex>a_2</tex>. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
=== Метод Рунге === | === Метод Рунге === | ||
Текущая версия
Содержание |
Введение
Метод Ньютона-Рафсона
Пусть имеется некоторая функция и необходимо найти такие значения аргумента
, для которых
Перепишем (1) в виде
и запишем -ое приближения корня (1.1), при этом делая поправку
к очередному значению
где и положим
.
Тогда (2) перепишется в виде
Нетрудно видеть, что (3) эквивалентно простому методу последовательных приближений
где .
Вспомним также, что если , то метод сходится. Имеем
Но так как справедливо соотношение (1.1), то для достаточно близких к решению (1.1), выражение в скобках в числителе дроби становится малым. Поэтому итерационный метод, описываемый формулой (3) сходится, если
- 1. Начальное приближение
выбрано достаточно близко к решению
.
- 2. Производная
не становится слишком большой.
- 3. Производная
не слишком близка к 1.
Это и есть метод Ньютона-Рафсона. Обычно его записывают в виде
,
где
Таким образом, мы вернулись к уравнению в форме (1), и условия сходимости принимают следующий вид
- 1. Начальное приближение
выбрано достаточно близко к корню уравнения
.
- 2. Производная
не становится очень большой.
- 3. Производная
не слишком близка к 0.
Случай почти равных корней
Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1 (масштаб сильно увеличен). Заметим, что производная близка
к 1 при x, равном обоим значениям корней,
и
. Более того, на основании теоремы Лагранжа, можно утверждать, что
где-то между
и
.
Рассмотрим, что случится, если принять в качестве исходного значения для корня
. Касательная,
проведенная через точку
, пересечет прямую
в точке
, и следующее приближение будет равно
. Касательная, проведенная через точку
, пересекает прямую в точке
, и в качестве следующего приближеня получается снова
. Итерационный процесс, таким образом, осциллирует между
и
до бесконечности, не сходясь ни к одному значению корня. Иначе говоря, не удается отделить эти два корня, потому что они расположены слишком близко.
Поэтому необходимо начальное приближение, достаточно близкое к искомому значению корня. Трудности возникают потому, что вычисление знаменателя в формуле (3) включает в себя вычитание двух почти равных чисел, что приводит к понижению точности.
Изложение метода
Поиск начального приближения
Сначала находится значение x, при котором , то есть решается уравнение
Пусть решением этого уравнения будет некоторое . Эта точка расположена между двумя корнями,
и
. Чтобы получить начальное приближение для решения уравнения, предположим, что
лежит посредине между
и
(рисунок 2). Другими словами, мы предполагаем, что
и
являются корнями уравнения (1.1). Разлагая
в ряд Тейлора в окрестности точки
и принимая во внимание, что
, получаем
Ограничим ряд тремя членами. Подставляя вместо
, имеем
Но по условию
поэтому, решая эти уравнения относительно , получаем
Таким образом, процесс решения сводится к следующему. Если дано уравнение с почти равными корнями, то, определив приблизительное местонахождение этих корней, необходиом решить уравнение
и определить значение . Для решения этого уравнения можно применить, например, метод Ньютона-Рафсона.
Найдя значение
, можно определить значение
. И, наконец, значения
и
используются в качестве начальных приближений для определения соответственно
и
.
Метод Рунге
Пусть существует асимптотическое разложение вида:
,
где - достаточно гладкая функция, а
.
Проведем расчеты на двух равномерных сетках с шагами и
соответственно и найдем выражения
и
,
. Потребуем,
чтобы погрешность для их линейной комбинации:
была величиной более высокого порядка по сравнению с и
. Если для
имеет место формула вида
,
то для
получим
Выберем параметр \sigma из условия :
.
Имеем
,
,
причем . Так, если
, то
. Таким образом, проведя вычисления на двух сетках
с шагами
и
, мы повысили порядок точности на
(на
) для
.
Процесс Эйткена
Метод расчета на нескольких сетках применяется для повышения порядка точности даже в том случае, когда неизвестен порядок главного члена погрешности. Предположим, чт для погрешности имеет место представление
,
,
так что
Проведем вычисления на трех сетках: ,
,
(
). Определим
. При этом пренебрегаем членом
. Образуем отношение
и найдем
.
Зная приближенное значение , можно методом методом Рунге повысить порядок точности. Для этого образуем комбинацию
и выберем
так, чтобы
, то есть
.
Тогда для погрешности
получаем
.
Числовой пример
Найдем с помощью квадратурной формулы трапеций приближенное значение интеграла, применив экстраполяцию Ричардсона (данный метод называется методом Ромберга):
В нижеследующей таблице представлены результаты работы программы:
| r | Исходная формула | Экстраполированная формула | Точное значение | Погрешность вычислений | Погрешность формулы |
|---|---|---|---|---|---|
| 2 | 3.98277278 | 4.04665506 | 4.04718956 | 0.0005345 | 0.00275556 |
| 4 | 4.03068449 | 4.04714980 | 4.04718956 | 0.00003976 | 0.00017222 |
| 8 | 4.04303347 | 4.04718692 | 4.04718956 | 0.00000264 | 0.00001076 |
| 16 | 4.04614856 | 4.04718939 | 4.04718956 | 0.00000017 | 0.00000067 |
| 32 | 4.04692918 | 4.04718955 | 4.04718956 | 0.00000001 | 0.00000004 |
| 64 | 4.04712446 | 4.04718956 | 4.04718956 | 0 | 0 |
| 20384 | 4.04718956 |
Здесь - коэффициент измельчения шага
. Исходная величина шага
.
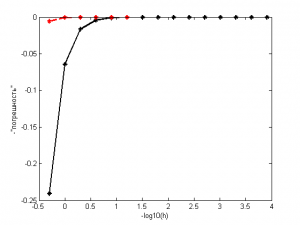
На иллюстрации черная сплошная линия - исходная формула, красная пунктирная - экстраполированная.
Как мы видим, разница между экстраполированными и неэкстраполированными результатами значительна. Уже при величине шага в мы можем найти значение интеграла с точностью
, тогда как в исходной формуле нам для достижения такой точности пришлось бы задать величину шага
.
Рекомендации программисту
Программируя экстраполяцию Ричардсона следует предпочесть итерацию рекурсии. Также реализуя многократное экстраполирование итеративно, нам не нужно хранить всю таблицу значений - достаточно иметь в распоряжении два последних столбца.
Заключение
Мы получили более точные результаты при меньшем количестве вычислений функции, чем в исходном методе. Избавившись от степени, составляющей ошибку, мы пришли к результату, который в противном случае был бы недостижим без значительного уменьшения размера шага. Таким образом, мы преобразовали весьма посредственный алгоритм вычисления интегралов в довольно эффективный.
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- Fundamental Methods of Numerical Extrapolation With Applications, mit.edu