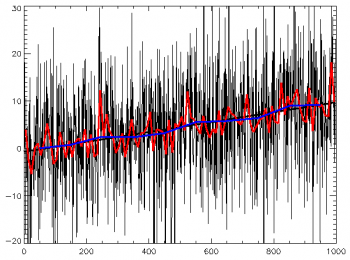
Временной ряд
Материал из MachineLearning.
(Исправлена опечатка в формуле - было T вместо Y) |
|||
| (7 промежуточных версий не показаны.) | |||
| Строка 37: | Строка 37: | ||
Как показано Боксом и Дженкинсом, модели временных рядов могут иметь различные формы и представлять различные стохастические процессы. | Как показано Боксом и Дженкинсом, модели временных рядов могут иметь различные формы и представлять различные стохастические процессы. | ||
При моделировании изменений уровня процесса можно выделить три широких класса имеющих практическую ценность: ''авторегрессионые модели'', ''интегральные модели'' и модели ''скользящего среднего''. Эти три класса линейно зависят от предшествующих данных. | При моделировании изменений уровня процесса можно выделить три широких класса имеющих практическую ценность: ''авторегрессионые модели'', ''интегральные модели'' и модели ''скользящего среднего''. Эти три класса линейно зависят от предшествующих данных. | ||
| - | На их основе построены модели [[ | + | На их основе построены модели [[авторегрессионное скользящее среднее|авторегрессионного скользящего среднего]] ([[Autoregressive Moving Average]], [[ARMA]]) и [[авторегрессионное интегрированное скользящее среднее|авторегрессионного интегрированного скользящего среднего]] ([[Autoregressive Integrated Moving Average]], [[ARIMA]]). |
Эти модели в свою очередь обобщает модель авторегрессионного дробноинтегрированного скользящего среднего ([[autoregressive fractionally integrated moving average]], [[ARFIMA]]). | Эти модели в свою очередь обобщает модель авторегрессионного дробноинтегрированного скользящего среднего ([[autoregressive fractionally integrated moving average]], [[ARFIMA]]). | ||
Расширения моделей на случаи, когда данные представляются не скалярно, а векторно, называют моделями многомерных временных рядов. | Расширения моделей на случаи, когда данные представляются не скалярно, а векторно, называют моделями многомерных временных рядов. | ||
| Строка 46: | Строка 46: | ||
Нелинейная зависимость уровня ряда от предыдущих точек интересна, отчасти из-за возможности генерации хаотических временных рядов. | Нелинейная зависимость уровня ряда от предыдущих точек интересна, отчасти из-за возможности генерации хаотических временных рядов. | ||
| - | Но главным всё же является то, что опытные исследования указывают на превосходство прогнозов, | + | Но главным всё же является то, что опытные исследования указывают на превосходство прогнозов, полученных от нелинейных модлей, над прогнозами линейных моделей. |
| - | Среди прочих типов нелинейных моделей временных рядов можно выделить модели, описывающие изменения | + | Среди прочих типов нелинейных моделей временных рядов можно выделить модели, описывающие изменения дисперсии ряда со временем (гетероскедатичность). |
| - | + | Такие модели называют моделями авторегрессионной условной гетероскедастичности ([[AutoRegressive Conditional Heteroscedasticity]], [[ARCH]]). | |
| - | К | + | К ним относится большое количество моделей: GARCH, TARCH, EGARCH, FIGARCH, CGARCH и др. |
В этих моделях изменения дисперсии связывают с ближайшими предшествующими данными. | В этих моделях изменения дисперсии связывают с ближайшими предшествующими данными. | ||
| - | + | Противовесом такому подходу является представление локально изменчивой дисперсии, при котором дисперсия может быть смоделирована зависящей от отдельного меняющегося со временем процесса, как в бистохастических моделях. | |
| - | В последнее время | + | В последнее время значительное внимание снискали исследования в области безмодельного анализа и методы, основанные на вейвлетных преобразованиях (например локально стационарные вейвлеты) в частности. |
Методы многомасштабного анализа разлагают заданный временной ряд на составные части, чтобы показать зависимость от времени с разным масштабом. | Методы многомасштабного анализа разлагают заданный временной ряд на составные части, чтобы показать зависимость от времени с разным масштабом. | ||
| Строка 61: | Строка 61: | ||
Существует большое число вариантов обозначения временных рядов. | Существует большое число вариантов обозначения временных рядов. | ||
Одним из типичных является <tex>X=\left{X_1,X_2,\dots \right}</tex>, обозначающее ряд с натуральными индексами. | Одним из типичных является <tex>X=\left{X_1,X_2,\dots \right}</tex>, обозначающее ряд с натуральными индексами. | ||
| - | Другое стандартное представление: <tex>Y=\left{Y_t:\:t\ | + | Другое стандартное представление: <tex>Y=\left{Y_t:\:t\in T\right}</tex> |
===Предположения=== | ===Предположения=== | ||
| Строка 75: | Строка 75: | ||
Общий вид авторегрессивной модели задаётся следующим образом: <br /> | Общий вид авторегрессивной модели задаётся следующим образом: <br /> | ||
| - | <tex>Y_t=\alpha_0+\alpha_1Y_{t-1}+\ | + | ::<tex>Y_t=\alpha_0+\alpha_1Y_{t-1}+\alpha_2Y_{t-2}+\dots+\alpha_pY_{t-p}+\epsilon_t</tex>, <br /> |
где <tex>\epsilon_t</tex> — источник случайность, белый шум. Белый шум имеет следующие свойства: | где <tex>\epsilon_t</tex> — источник случайность, белый шум. Белый шум имеет следующие свойства: | ||
#<tex>E\left[\epsilon_t\right]=0</tex> | #<tex>E\left[\epsilon_t\right]=0</tex> | ||
#<tex>E\left[\epsilon^2_t\right]=\sigma^2</tex> | #<tex>E\left[\epsilon^2_t\right]=\sigma^2</tex> | ||
| - | #<tex>E\left[\epsilon_t\epsilon_s\right]=0\; | + | #<tex>E\left[\epsilon_t\epsilon_s\right]=0\; t\not= s</tex> <br /> |
В этих предположениях процесс определён вплоть до моментов второго порядка и, при определённых условиях на коэффициенты, может быть стационарным в широком смысле. | В этих предположениях процесс определён вплоть до моментов второго порядка и, при определённых условиях на коэффициенты, может быть стационарным в широком смысле. | ||
| Строка 85: | Строка 85: | ||
==См. также== | ==См. также== | ||
| + | *[[Временной ряд (библиотека примеров)]] | ||
*[[Преобразование Фурье]] | *[[Преобразование Фурье]] | ||
*[[Метод главных компонент]] | *[[Метод главных компонент]] | ||
| Строка 108: | Строка 109: | ||
[[Категория:Прикладная статистика]] | [[Категория:Прикладная статистика]] | ||
[[Категория:Регрессионный анализ]] | [[Категория:Регрессионный анализ]] | ||
| + | [[Категория:Анализ временных рядов]] | ||
Текущая версия
В статистике, обработке сигналов и многих других областях под временным рядом понимаются последовательно измеренные через некоторые (зачастую равные) промежутки времени данные. Анализ временных рядов объединяет методы изучения временных рядов, как пытающиеся понять природу точек данных (откуда они взялись? что их породило?), так и пытающиеся построить прогноз. Прогнозирование временных рядов заключается в построении модели для предсказания будущих событий основываясь на известных событий прошлого, предсказания будущих данных до того как они будут измерены. Типичный пример — предсказание цены открытия биржи основываясь на предыдущей её деятельности.
Понятие анализ временных рядов используется для того, чтобы отделить эту задачу от в первую очередь от более простых задач анализа данных (когда нет естественного порядка поступления наблюдений) и, во-вторых, от анализа пространственных данных, в котором наблюдения зачастую связаны с географическим положением. Модель временного ряда в общем смысле отражает идею, что близкие во времени наблюдения будут теснее связаны, чем удалённые. Кроме того, модели временных рядов зачастую используют однонаправленный порядок по времени в том смысле, что значения в ряду выражаются в некотором виде через прошлые значения, а не через последующие (см. обратимость времени).
Методы анализа временных рядов зачастую делят на два класса: анализ в частотной области и анализ во временной области. Первый основывается на спектральном анализе и с недавних пор вейвлетном анализе, и может рассматриваться в качестве не использующих модели методов анализа, хорошо подходящих для исследований на этапе разведки. Методы анализа во временной области также имеют безмодельное подмножество, состоящее из кросс-корреляционного анализа и автокорреляционного анализа, но именно здесь появляются частично и полностью определённые модели временных рядов.
Содержание |
Анализ временных рядов
Существует несколько методов анализа данных, применимых для временных рядов.
Общее исследование
- Визуальное изучение графических представлений временных рядов
- Автокорреляционный анализ для изучения зависимостей
- Спектральный анализ для изучения циклического поведения, не связанного с сезонностью
Описание
- Разделение компонент: тренд, сезонность, медленно и быстро меняющиеся компоненты, циклическая нерегулярность
- Простейшие свойства частных распределений
Прогнозирование и предсказание
- Полноценные статистические модели при стохастическом моделировании для создания альтернативных версий временных рядов, показывающих, что могло бы случиться на произвольных отрезках времени в будущем (предсказание)
- Упрощённые или поноценные статистические модели для описания вероятные значения временного ряда в ближайшем будущем при известных последних значениях (прогноз)
Модели временных рядов
Как показано Боксом и Дженкинсом, модели временных рядов могут иметь различные формы и представлять различные стохастические процессы. При моделировании изменений уровня процесса можно выделить три широких класса имеющих практическую ценность: авторегрессионые модели, интегральные модели и модели скользящего среднего. Эти три класса линейно зависят от предшествующих данных. На их основе построены модели авторегрессионного скользящего среднего (Autoregressive Moving Average, ARMA) и авторегрессионного интегрированного скользящего среднего (Autoregressive Integrated Moving Average, ARIMA). Эти модели в свою очередь обобщает модель авторегрессионного дробноинтегрированного скользящего среднего (autoregressive fractionally integrated moving average, ARFIMA). Расширения моделей на случаи, когда данные представляются не скалярно, а векторно, называют моделями многомерных временных рядов. Для таких моделей в сокращённых названиях появляется буква «v» от слова «vector». Существуют расширения моделей на случай, когда исследуемый временной ряд является ведомым для некоторого «вынуждающего» ряда (который, однако, может не быть причиной возникновения исследуемого ряда). Отличие от многомерного ряда заключается в том, что вынуждающий ряд может быть детерминированным или управляться исследователем, проводящим эксперимент. Для таких моделей в сокращении появляется буква «x» от «exogenous» (экзогенный, вызываемый внешними причинами).
Нелинейная зависимость уровня ряда от предыдущих точек интересна, отчасти из-за возможности генерации хаотических временных рядов. Но главным всё же является то, что опытные исследования указывают на превосходство прогнозов, полученных от нелинейных модлей, над прогнозами линейных моделей.
Среди прочих типов нелинейных моделей временных рядов можно выделить модели, описывающие изменения дисперсии ряда со временем (гетероскедатичность). Такие модели называют моделями авторегрессионной условной гетероскедастичности (AutoRegressive Conditional Heteroscedasticity, ARCH). К ним относится большое количество моделей: GARCH, TARCH, EGARCH, FIGARCH, CGARCH и др. В этих моделях изменения дисперсии связывают с ближайшими предшествующими данными. Противовесом такому подходу является представление локально изменчивой дисперсии, при котором дисперсия может быть смоделирована зависящей от отдельного меняющегося со временем процесса, как в бистохастических моделях.
В последнее время значительное внимание снискали исследования в области безмодельного анализа и методы, основанные на вейвлетных преобразованиях (например локально стационарные вейвлеты) в частности. Методы многомасштабного анализа разлагают заданный временной ряд на составные части, чтобы показать зависимость от времени с разным масштабом.
Обозначения
Существует большое число вариантов обозначения временных рядов.
Одним из типичных является , обозначающее ряд с натуральными индексами.
Другое стандартное представление:
Предположения
Существуют две группы предположений, в условиях которых строится большинство теорий:
- Стационарность процесса
- Эргодичность
Идея стационарности трактуется в широком смысле, охватывая две основных идеи: строгая стационарность и стационарность ворого порядка (стационарность в широком смысле). На основании этих предложений могут быть построены и модели, и приложения, хотя модели в дальнейшем могут рассматриваться как частично заданные.
Анализ временного ряда может проводиться и когда ряд сезонно стацонарен или нестационарен.
Модели
Общий вид авторегрессивной модели задаётся следующим образом:
,
где — источник случайность, белый шум. Белый шум имеет следующие свойства:
В этих предположениях процесс определён вплоть до моментов второго порядка и, при определённых условиях на коэффициенты, может быть стационарным в широком смысле.
Если шумы имеют нормальное распределение, их называют нормальным белым шумом. В этом случае авторегрессионный процесс может быть строго стационрен, опять же, при выполенении некоторых условий на коэффициенты.
См. также
- Временной ряд (библиотека примеров)
- Преобразование Фурье
- Метод главных компонент
- Спектральный анализ
- Автокорреляция
- Скользящее среднее
- Линейный прогноз
- Хаотический анализ
Ссылки
Литература
- Box, George; Jenkins, Gwilym Time series analysis: forecasting and control, rev. ed. // Oakland, California: Holden-Day. — 1976.