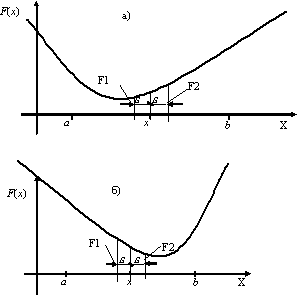Метод дихотомии
Материал из MachineLearning.
(→Изложение метода) |
(→Метод дихотомии как метод оптимизации) |
||
| Строка 116: | Строка 116: | ||
'''''Однопараметрическая оптимизация''''' (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных. | '''''Однопараметрическая оптимизация''''' (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных. | ||
| - | Рассмотрим метод дихотомии как простейший однопараметрический метод безусловной оптимизации. Данный метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции. | + | Рассмотрим метод дихотомии как простейший однопараметрический метод безусловной оптимизации. Данный метод является ''методом прямого поиска''. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции. |
Дана функция <tex>F(x)</tex>. Необходимо найти <tex>\overline{x}</tex>, доставляющий минимум (или максимум) функции <tex>F(x)</tex> на интервале <tex>[a,b]</tex> с заданной точностью <tex>\varepsilon</tex>, т.е. найти | Дана функция <tex>F(x)</tex>. Необходимо найти <tex>\overline{x}</tex>, доставляющий минимум (или максимум) функции <tex>F(x)</tex> на интервале <tex>[a,b]</tex> с заданной точностью <tex>\varepsilon</tex>, т.е. найти | ||
| - | <tex>\overline{x} = \arg \min F(x), \; \overline{x} \in [a,b]</tex>. | + | ::<tex>\overline{x} = \arg \min F(x), \; \overline{x} \in [a,b]</tex>. |
| + | |||
| + | [[Изображение:09 01.gif|frame|Рис. 1. Поиск экстремума функции <tex>F(x)</tex> методом дихотомии]] | ||
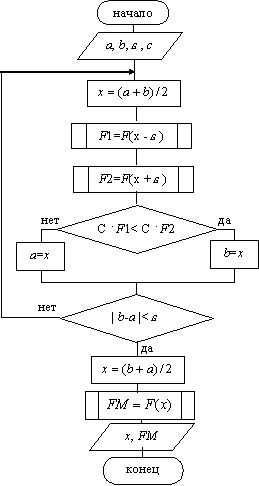
| + | [[Изображение:09 02.gif|frame|Рис. 2. Схема алгоритма метода дихотомии]] | ||
Запишем словесный алгоритм метода. | Запишем словесный алгоритм метода. | ||
| + | |||
| + | |||
#На каждом шаге процесса поиска делим отрезок <tex>[a,b]</tex> пополам, <tex>x=\frac {a+b}{2}</tex> - координата середины отрезка <tex>[a,b]</tex>. | #На каждом шаге процесса поиска делим отрезок <tex>[a,b]</tex> пополам, <tex>x=\frac {a+b}{2}</tex> - координата середины отрезка <tex>[a,b]</tex>. | ||
| - | #Вычисляем значение функции <tex>F(x)</tex> в окрестности <tex>\pm \varepsilon</tex> вычисленной точки <tex>x</tex>, т.е. <tex>F_1=F(x-\varepsilon),\; F_2=F(x+\varepsilon)</tex>. | + | #Вычисляем значение функции <tex>F(x)</tex> в окрестности <tex>\pm \varepsilon</tex> вычисленной точки <tex>x</tex>, т.е. <br |
| - | #Сравниваем <tex>F_1</tex> и <tex>F_2</tex> и отбрасываем одну из половинок отрезка <tex>[a,b]</tex> (рис | + | \> <tex>F_1=F(x-\varepsilon),\; F_2=F(x+\varepsilon)</tex>. |
| - | #*При поиске минимума: | + | #Сравниваем <tex>F_1</tex> и <tex>F_2</tex> и отбрасываем одну из половинок отрезка <tex>[a,b]</tex> (рис. 1). |
| + | #*При поиске минимума: | ||
| + | #**Если <tex>F_1<F_2</tex>, то отбрасываем отрезок <tex>[x,b]</tex>, тогда <tex>b=x</tex>. (рис. 1.а) | ||
| + | #**Иначе отбрасываем отрезок <tex>[a,x]</tex>, тогда <tex>a=x</tex>. (рис. 1.б) | ||
#*При поиске максимума: | #*При поиске максимума: | ||
| - | + | #**Если <tex>F_1<F_2</tex>, то отбрасываем отрезок <tex>[a,x]</tex>, тогда <tex>a=x</tex>. | |
| - | + | #**Иначе отбрасываем отрезок <tex>[x,b]</tex>, тогда <tex>b=x</tex>. | |
#Деление отрезка <tex>[a,b]</tex> продолжается, пока его длина не станет меньше заданной точности <tex>\varepsilon</tex>, т.е. <tex>|b-a| \le \varepsilon</tex>. | #Деление отрезка <tex>[a,b]</tex> продолжается, пока его длина не станет меньше заданной точности <tex>\varepsilon</tex>, т.е. <tex>|b-a| \le \varepsilon</tex>. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| + | Схема алгоритма метода дихотомии представлена на рис 2. | ||
| - | + | На рис 2: | |
| - | + | ::<tex>c</tex>- константа, | |
| + | ::<tex>c =\begin{cases} \quad 1 , \quad (min \; F(x)), \\-1, \quad (max \; F(x)). \end{cases}</tex> | ||
| - | + | При выводе <tex>x</tex> – координата точки, в которой функция <tex>F(x)</tex> имеет минимум (или максимум), <tex>F_M</tex> – значение функции <tex>F(x)</tex> в этой точке. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== Список литературы == | == Список литературы == | ||
Версия 17:51, 23 ноября 2008
Содержание |
Введение
Метод дихотомии - достаточно широко используемый метод поиска, известный также как метод бисекции или метод половинного деления.
- Во-первых, это один из простых способов поиска корней функции одного аргумента.
- Во-вторых, метод дихотомии применяется для нахождения значений действительно-значной функции, определяемому по какому-либо критерию (это может быть сравнение на минимум, максимум или конкретное число).
Метод дихотомии как метод поиска корней функции
Изложение метода
Перед применением метода дихотомии для поиска корней функции необходимо отделить корни одним из известных способов, например, графическим методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке нужно искать корень.
Будем считать, что корень функции
отделён на отрезке
. Задача заключается в том, чтобы найти и уточнить этот корень методом половинного деления (дихотомии). Другими словами, требуется найти приближённое значение корня с заданной точностью
.
Пусть функция непрерывна на отрезке
,
и
- единственный корень уравнения
.
(Мы не рассматриваем случай, когда корней на отрезке несколько, то есть более одного. В качестве
можно взять и другое достаточно малое положительное число, например,
.)
Поделим отрезок пополам. Получим точку
и два отрезка
.
- Если
, то корень
найден (
).
- Если нет, то из двух полученных отрезков
и
надо выбрать один
такой, что
, то есть
, если
или
, если
.
- Новый отрезок
делим пополам. Получаем середину этого отрезка
и так далее.
Для того, чтобы найти приближённое значение корня с точностью до , необходимо остановить процесс половинного деления на таком шаге
, на котором
и вычислить
. Тогда можно взять
.
Реализация метода на С++ и числовой пример
Решим уравнение методом дихотомии. Графическим методом находим отрезок
, которому принадлежит искомый корень. Так как
, то принимаем
.
Ниже приведен пример программы на Си++, которая решает поставленную задачу.
Программа 1. Корень уравнения
#include <iostream> #include <cmath> using namespace std; const double epsilon = 1e-2; double f(double x) { return 4- exp(x) - 2*x^2; } int main() { double a, b, c; a = 0; b = 2; while (b - a > epsilon){ c = (a + b) / 2; if(f(b) * f(c) < 0) a = c; else b = c; } cout << (a + b) / 2 << endl; return 0; }
Искомый корень . Вычисления проводились с точностью
.
Промежуточные вычисления представлены в таблице ниже.
| n | an | bn | cn | bn-cn |
|---|---|---|---|---|
| 1 | 0 | 1 | 0.5 | 0.5 |
| 2 | 0.5 | 1 | 0.75 | 0.25 |
| 3 | 0.75 | 1 | 0.875 | 0.125 |
| 4 | 0.875 | 1 | 0.9375 | 0.0625 |
| 5 | 0.875 | 0.9375 | 0.90625 | 0.03125 |
| 6 | 0.875 | 0.90625 | 0.890625 | 0.015625 |
| 7 | 0.875 | 0.890625 | 0.8828125 | 0.0078125 |
Метод дихотомии как метод оптимизации
Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.
Рассмотрим метод дихотомии как простейший однопараметрический метод безусловной оптимизации. Данный метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Дана функция . Необходимо найти
, доставляющий минимум (или максимум) функции
на интервале
с заданной точностью
, т.е. найти
.
Запишем словесный алгоритм метода.
- На каждом шаге процесса поиска делим отрезок
пополам,
- координата середины отрезка
.
- Вычисляем значение функции
в окрестности
вычисленной точки
, т.е.
.
- Сравниваем
и
и отбрасываем одну из половинок отрезка
(рис. 1).
- При поиске минимума:
- Если
, то отбрасываем отрезок
, тогда
. (рис. 1.а)
- Иначе отбрасываем отрезок
, тогда
. (рис. 1.б)
- Если
- При поиске максимума:
- Если
, то отбрасываем отрезок
, тогда
.
- Иначе отбрасываем отрезок
, тогда
.
- Если
- При поиске минимума:
- Деление отрезка
продолжается, пока его длина не станет меньше заданной точности
, т.е.
.
Схема алгоритма метода дихотомии представлена на рис 2.
На рис 2:
- константа,
При выводе – координата точки, в которой функция
имеет минимум (или максимум),
– значение функции
в этой точке.
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
- http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
- http://www.intuit.ru/department/calculate/calcmathbase/1/4.html