Метод Ньютона. Метод Стеффенсена

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 8: Строка 8:
Рассмотирим метод Ньютона для задачи
Рассмотирим метод Ньютона для задачи
-
{{ eqno || 1 }}
+
{{ eqno | 1 }}
<tex> J(u)-> \inf; u \in U,</tex>
<tex> J(u)-> \inf; u \in U,</tex>
Строка 17: Строка 17:
Возьмем квадратичную часть этого приращения
Возьмем квадратичную часть этого приращения
-
{{ eqno || 2 }}
+
{{ eqno | 2 }}
<tex> J_k(u)=<J'(u_k),u-u_k>+1/2*<J''(u_k)(u-u_k),u-u_k> </tex>
<tex> J_k(u)=<J'(u_k),u-u_k>+1/2*<J''(u_k)(u-u_k),u-u_k> </tex>
Строка 23: Строка 23:
и определим вспомогательное приближение <tex>u_k</tex> из условий
и определим вспомогательное приближение <tex>u_k</tex> из условий
-
{{ eqno || 3 }}
+
{{ eqno | 3 }}
<tex>u_k \in U, J_k(u_k)=\inf_U J_k(u).</tex>
<tex>u_k \in U, J_k(u_k)=\inf_U J_k(u).</tex>
Строка 29: Строка 29:
Следущее (k+1)-e приближение будем искать в виде
Следущее (k+1)-e приближение будем искать в виде
-
{{ eqno || 4 }}
+
{{ eqno | 4 }}
<tex>u_{k+1}=u_k+\alpha_k(\overline{u_k}-u_k), 0<\alpha_k<1. </tex>
<tex>u_{k+1}=u_k+\alpha_k(\overline{u_k}-u_k), 0<\alpha_k<1. </tex>
В зависимости от способа выбора величины <tex>\alpha_k</tex> в (4) можно получить различные варианты метода Ньютона. Укажем несколько наиболее употребительных способов выбора <tex>\alpha_k</tex>.
В зависимости от способа выбора величины <tex>\alpha_k</tex> в (4) можно получить различные варианты метода Ньютона. Укажем несколько наиболее употребительных способов выбора <tex>\alpha_k</tex>.
-
===1)===
+
===1)<tex>\alpha_k=1</tex> ===
-
{{ eqno || 5 }}
+
{{ eqno | 5 }}
-
<tex>\alpha_k=1, k=0,1,\dots </tex>
+
<tex>\alpha_k=1, k=0,1,\dots </tex>
Тогда <tex>u_{k+1}=\overline{u_k} (k=0,1,\dots)</tex>, т. е. условие (3) сразу определяет следующее (k+1)-е приближение. Иначе говоря,
Тогда <tex>u_{k+1}=\overline{u_k} (k=0,1,\dots)</tex>, т. е. условие (3) сразу определяет следующее (k+1)-е приближение. Иначе говоря,
-
<tex> u_{k+1}\in U, J_k(u_{k+1})=\inf\limits_U J_k(u), k=0,1,\dots </tex>
+
{{ eqno | 6 }}
 +
<tex> u_{k+1}\in U, J_k(u_{k+1})=\inf\limits_U J_k(u), k=0,1,\dots </tex>
-
Таким образом получаем систему линейный уровнений, которую необходимо решать на каждой итерации.
+
Таким образом получаем систему линейных уровнений относительно <tex>u_{k+1}-u_k</tex>, которую необходимо решать на каждой итерации.
 +
{{ eqno | 7 }}
<tex> J'_k(u_{k+1})=J'(u_k)+J''(u_k)(u_{k+1}-u_k)=0. </tex>
<tex> J'_k(u_{k+1})=J'(u_k)+J''(u_k)(u_{k+1}-u_k)=0. </tex>
 +
 +
Если матрица <tex>J''(u_k)</tex> невырожденная, то имеем
 +
 +
{{ eqno | 8 }}
 +
<tex> u_{k+1}=u_k-(J''(u_k))^{-1}J'(u_k), k=0,1,\dots </tex>
 +
 +
===2) <tex>\alpha_k=\lambda^{i_0}</tex>===
 +
<tex>i_0</tex> - минимальный среди i>0 номер, для которых выполнено неравенство
 +
 +
<tex>J(u_k)-J(u_k+\lambda^i(\overline{u_k}-u_k))\ge \eps \lambda^i |J_k(\overline(u_k))|,<tex>
 +
 +
где <tex>\lambda</tex>,ε - параметры метода, 0<λ, ε<1.
 +
===3)===
 +
<tex></tex>

Версия 18:33, 23 ноября 2008

Содержание

Постановка задачи

Общие понятния

Если минимизируемая функция дважд непрерывно дифференцируема и производные J'(u), J''(u) просто вычисляются, то можно применять методы минимизации второго порядка, которые используют квадратичную часть разложения функции в ряд Тейлора. Поскольку квадратичная часть разложения аппроксимирует функцию гораздо точнее, чем линейная, то естесвенно ожидать, что методв второго порядка сходятся быстрее, чем методы первого. Метод Ньютона, имеющий квадратичную скорость сходимости на классе сильно выпуклых функций. Говорят, что последовательность {u_k}сходитcz к u_* с линейной скоростью или со скоростью геометрической прогресси (со знаменателем q), если начиная с некоторго номера, выполняется неравенство |u_{k+1}-u_*|<q|u_k-u_*| (0<q<1); при выполнении неравенства |u_{k+1}-u_*|<q_k|u_k-u_*|, где {q_k}->0, говорят о сверхлинейной скорости сходимости последованояти {u_k} к u_*, а если здесь q_k=C|u_k-u_*|^{s-1}, т. е. |u_{k+1}-u_*|<C|u_k-u_*|^s, то говорят о скорости сходимсоти порядка s. При s=2, говорят о квадратичной скорости сходимости.

Метод Ньютона

Рассмотирим метод Ньютона для задачи

( 1 )

J(u)-> \inf; u \in U, где J(u) _in C^2(U), U - выпуклое замкнутое множество из E^n. Пусть u_0∈U - некоторое начальное приближение. Если известно k-е приближение u_k, то приращение функции J(u)∈ C^2(U) в точек u_k можно представить в виде

J(u)-J(u_k)=<J'(u_k),u-u_k>+1/2*<J''(u_k)(u-u_k),u-u_k>+o(|u-u_k|^2)

Возьмем квадратичную часть этого приращения

( 2 )

J_k(u)=<J'(u_k),u-u_k>+1/2*<J''(u_k)(u-u_k),u-u_k>

и определим вспомогательное приближение u_k из условий

( 3 )

u_k \in U, J_k(u_k)=\inf_U J_k(u).

Следущее (k+1)-e приближение будем искать в виде

( 4 )

u_{k+1}=u_k+\alpha_k(\overline{u_k}-u_k), 0<\alpha_k<1.

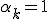
В зависимости от способа выбора величины \alpha_k в (4) можно получить различные варианты метода Ньютона. Укажем несколько наиболее употребительных способов выбора \alpha_k.

1)\alpha_k=1

( 5 )

\alpha_k=1, k=0,1,\dots Тогда u_{k+1}=\overline{u_k} (k=0,1,\dots), т. е. условие (3) сразу определяет следующее (k+1)-е приближение. Иначе говоря,

( 6 )

u_{k+1}\in U, J_k(u_{k+1})=\inf\limits_U J_k(u), k=0,1,\dots

Таким образом получаем систему линейных уровнений относительно u_{k+1}-u_k, которую необходимо решать на каждой итерации.

( 7 )

J'_k(u_{k+1})=J'(u_k)+J''(u_k)(u_{k+1}-u_k)=0.

Если матрица J''(u_k) невырожденная, то имеем

( 8 )

u_{k+1}=u_k-(J''(u_k))^{-1}J'(u_k), k=0,1,\dots

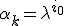
2) \alpha_k=\lambda^{i_0}

i_0 - минимальный среди i>0 номер, для которых выполнено неравенство

J(u_k)-J(u_k+\lambda^i(\overline{u_k}-u_k))\ge \eps \lambda^i |J_k(\overline(u_k))|,<tex> </p><p>где <tex>\lambda,ε - параметры метода, 0<λ, ε<1.

3)

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0._%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%A1%D1%82%D0%B5%D1%84%D1%84%D0%B5%D0%BD%D1%81%D0%B5%D0%BD%D0%B0»
Личные инструменты