Логит-анализ
Материал из MachineLearning.
| Строка 11: | Строка 11: | ||
<tex>f(z)=\frac{1}{1+e^{-z}}</tex> | <tex>f(z)=\frac{1}{1+e^{-z}}</tex> | ||
| + | |||
| + | |||
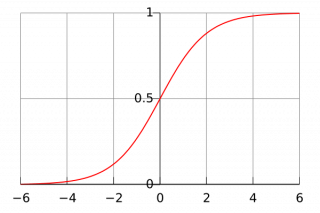
| + | Типичный график логистической функции показан на рис. 1. По оси абсцисс – управляющий параметр z ("Вход"), по оси ординат f(z) - "отклик". Логистическая функция полезна, потому что она может принимать любые входные значения от минус бесконечности до плюс бесконечности, тогда как отклик (функция) ограничена диапазоном [0; 1]. Переменная z отражает подверженность некоторому набору факторов риска, в то время как f (z) представляет вероятность конкретного исхода, при заданном наборе рисков. Переменная z является мерой полного вклада всех факторов риска, используемых в модели, и известна как logit. | ||
| + | |||
| + | <tex>z=\beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + \cdots + \beta_kx_k,</tex> | ||
Версия 04:18, 10 января 2009
В статистике логистическая регрессия - модель, используемая для предсказания вероятности возникновения события «подгоном» данных к логистической кривой. При этом используют несколько предсказывающих переменных, которые могут быть или числовыми или категориальными. Например, вероятность, того, что у человека случится сердечный приступ в определенный период времени, может быть предсказана в зависимости от возраста человека, пола и индекса массы тела. Логистическая регрессия широко используется в медицинских и общественных науках, так же в маркетинговых исследованиях, таких как предсказание склонности клиента купить определенный продукт или прекратить подписку.
Другие названия для логистической регрессии, используемые в различных прикладных областях, включают логистическую модель, Логит-модель, и классификатор максимальной энтропии.
Логистическая регрессия относится к классу моделей, известных как обобщенные линейные модели.
Простое объяснение
Объяснение логистической регрессии начинается с объяснения логистической функции:
Типичный график логистической функции показан на рис. 1. По оси абсцисс – управляющий параметр z ("Вход"), по оси ординат f(z) - "отклик". Логистическая функция полезна, потому что она может принимать любые входные значения от минус бесконечности до плюс бесконечности, тогда как отклик (функция) ограничена диапазоном [0; 1]. Переменная z отражает подверженность некоторому набору факторов риска, в то время как f (z) представляет вероятность конкретного исхода, при заданном наборе рисков. Переменная z является мерой полного вклада всех факторов риска, используемых в модели, и известна как logit.