Функция интенсивности рисков

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Функция интенсивности рисков в непрерывном случае)
Строка 19: Строка 19:
:<tex>P(\mathbf{T}\le t)=F(t)=1-R(t),\quad t\ge 0. \!</tex>,
:<tex>P(\mathbf{T}\le t)=F(t)=1-R(t),\quad t\ge 0. \!</tex>,
-
где <tex>{T}</tex> - время отказа.
+
где <tex>T</tex> - время отказа.
'''Функции распределения рисков''' соответствует некоторая функция плотности вероятности
'''Функции распределения рисков''' соответствует некоторая функция плотности вероятности

Версия 14:23, 11 января 2009

Функция интенсивности рисков \lambda (t) (этот термин был впервые использован в работе Barlow, 1963) определяется как вероятность того, что объект, выживший к началу соответствующего интервала, откажет или умрет в течение этого интервала.

Содержание

Функция интенсивности в дискретном случае

В дискретном случае функция интенсивности рисков \lambda (t) понимается как вероятность того, что поломка или смерть произошла в интервале времени [t, t + \triangle t]. Функцию плотности рисков можно определить с помощью функции выживаемости R(t), которая показывает вероятность отсутствия отказов до момента времени t :

\lambda(t) = \frac{R(t)-R(t+\triangle t)}{\triangle t R(t)}

Появление R(t) в знаменателе объясняется тем, что фактически рассматривается условная вероятность.

Функция интенсивности рисков в непрерывном случае

Экспоненциальные функции плотности рисков
Экспоненциальные функции плотности рисков

Вычисляя дискретную функцию интенсивности рисков для всё меньших интервалов времени \Delta t , мы получим ее непрерывный аналог:

h(t)=\lim_{\triangle t \to 0} \frac{R(t)-R(t+\triangle t)}{\triangle t \cdot R(t)}.

Непрерывная Функция интенсивности рисков зависит от Функции распределения рисков F(t), которая описывает вероятность отказа к моменту времени t:

P(\mathbf{T}\le t)=F(t)=1-R(t),\quad t\ge 0. \!,

где T - время отказа.

Функции распределения рисков соответствует некоторая функция плотности вероятности f(x),

F(t)=\int_{0}^{t} f(x)\, dx. \!

Теперь функцию интенсивности рисков можно определить следующим образом:

h(t)=\frac{f(t)}{R(t)}. \!

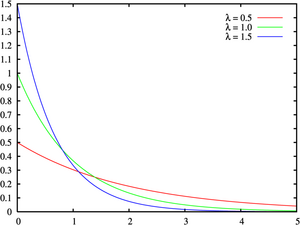
В качестве модели функции распределения рисков можно использовать различные известные функции распределения. Обычная модель - это экспоненциальное распределение рисков,

F(t)=\int_{0}^{t} \lambda e^{-\lambda x}\, dx = 1 - e^{-\lambda t}, \!,

основанное на экспоненциальном распределении.

h(t) = \frac{f(t)}{R(t)} = \frac{\lambda e^{-\lambda x}}{e^{-\lambda x}} = \lambda

Как мы видим, при экспоненциальной функции распределения рисков функция плотности рисков оказывается константой (в таком случае говорят, что распределение не имеет 'памяти').

Смотри также

Источники

  • Kapur, K.C., and Lamberson, L.R., (1977), Reliability in Engineering Design, pp 8-30, John Wiley & Sons, New York.

Внешние ссылки

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%B8%D0%BD%D1%82%D0%B5%D0%BD%D1%81%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%D1%80%D0%B8%D1%81%D0%BA%D0%BE%D0%B2»
Личные инструменты