Следящий контрольный сигнал
Материал из MachineLearning.
(→Критерий адекватности модели) |
|||
| Строка 1: | Строка 1: | ||
{{TOCright}} | {{TOCright}} | ||
| - | + | При использовании модели прогнозирования временного ряда встаёт проблема адекватности этой модели. | |
| - | Пусть <tex>\eps_t=y_t-\hat{y}_t</tex>, где <tex>y_t</tex> - данные, которые уже | + | Пусть <tex>\eps_t=y_t-\hat{y}_t</tex>, где <tex>y_t</tex> - данные, которые уже известны, <tex>\hat{y}_t</tex>- прогноз на момент t, полученный с помощью некоторой адаптивной модели. |
| - | + | Если ошибка <tex>\eps_t</tex> невелика, т.е. разница между реальными данными и прогнозом мала, то использование данной модели оправдано. | |
== Определение == | == Определение == | ||
<tex>K_t = \frac{\hat{\eps}_t}{\tilde{\eps}_t}</tex> - скользящий контрольный сигнал. | <tex>K_t = \frac{\hat{\eps}_t}{\tilde{\eps}_t}</tex> - скользящий контрольный сигнал. | ||
| + | |||
| + | Рекуррентная формула вычисления ошибок: | ||
<tex>\hat{\eps}_t = \gamma \eps_t + (1-\gamma) \hat{\eps}_{t-1}</tex>; | <tex>\hat{\eps}_t = \gamma \eps_t + (1-\gamma) \hat{\eps}_{t-1}</tex>; | ||
| Строка 12: | Строка 14: | ||
где <tex>\gamma \in (0,1)</tex>, рекомендуется брать <tex>\gamma \in[0.05,0.1]. </tex> | где <tex>\gamma \in (0,1)</tex>, рекомендуется брать <tex>\gamma \in[0.05,0.1]. </tex> | ||
| - | |||
== Гипотеза адекватности модели == | == Гипотеза адекватности модели == | ||
| - | + | <tex>H_0</tex>: модель адекватна. | |
| + | |||
| + | <tex> E \eps_t = 0,\; E \eps_t \eps_{t+d} = 0, \; d \geq 1</tex> | ||
При <tex>\gamma \leq 0.1, \; t \rightarrow \inf, \; \hat{\eps}_t \sim N(0,\sigma^2 \frac{\gamma}{2-\gamma}), \; \sigma^2 = E\eps^2_t</tex> - дисперсия шума. <tex> \hat{\eps}_t \approx \sigma/1.2</tex>. | При <tex>\gamma \leq 0.1, \; t \rightarrow \inf, \; \hat{\eps}_t \sim N(0,\sigma^2 \frac{\gamma}{2-\gamma}), \; \sigma^2 = E\eps^2_t</tex> - дисперсия шума. <tex> \hat{\eps}_t \approx \sigma/1.2</tex>. | ||
| - | + | ||
| - | [[Изображение:NormalDistribCrop.png|180px|thumb| | + | [[Изображение:NormalDistribCrop.png|180px|thumb|Если значение <tex>K_t</tex> попадает в серую область, ограниченную [[Доверительный интервал| доверительным интервалом]] с уровнем α, то гипотеза выполняется. ]] |
| - | Модель | + | Модель адекватна (гипотеза <tex>H_0</tex> принимается), если скользящий контрольный сигнал |
<tex>K_t \in \left[-1.2 \Phi_{\frac{\alpha}{2}} \sqrt{\frac{\gamma}{2-\gamma}}, \; 1.2 \Phi_{1-\frac{\alpha}{2}} \sqrt{\frac{\gamma}{2-\gamma} \right]</tex>. | <tex>K_t \in \left[-1.2 \Phi_{\frac{\alpha}{2}} \sqrt{\frac{\gamma}{2-\gamma}}, \; 1.2 \Phi_{1-\frac{\alpha}{2}} \sqrt{\frac{\gamma}{2-\gamma} \right]</tex>. | ||
| Строка 34: | Строка 37: | ||
[[Модель Тейла-Вейджа]] — учитываются аддитивный тренд и сезонность. | [[Модель Тейла-Вейджа]] — учитываются аддитивный тренд и сезонность. | ||
| - | + | ||
[[Категория:Прикладная статистика]] | [[Категория:Прикладная статистика]] | ||
[[Категория:Энциклопедия анализа данных]] | [[Категория:Энциклопедия анализа данных]] | ||
Версия 17:48, 11 января 2009
|
При использовании модели прогнозирования временного ряда встаёт проблема адекватности этой модели.
Пусть , где
- данные, которые уже известны,
- прогноз на момент t, полученный с помощью некоторой адаптивной модели.
Если ошибка
невелика, т.е. разница между реальными данными и прогнозом мала, то использование данной модели оправдано.
Определение
- скользящий контрольный сигнал.
Рекуррентная формула вычисления ошибок:
;
;
где , рекомендуется брать
Гипотеза адекватности модели
: модель адекватна.
При - дисперсия шума.
.
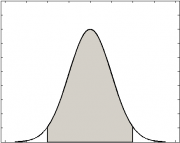
Модель адекватна (гипотеза принимается), если скользящий контрольный сигнал
.
Литература
Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования временных рядов. — М.: Финансы и статистика, 2003.
Ссылки
Модель Брауна - экспоненциальное сглаживание.
Модель Хольта — учитываются линейный тренд без сезонности.
Модель Хольта-Уинтерса — учитываются мультипликативный тренд и сезонность.
Модель Тейла-Вейджа — учитываются аддитивный тренд и сезонность.

