Человек - генератор случайных чисел?
Материал из MachineLearning.
(→Способ решения) |
|||
| Строка 41: | Строка 41: | ||
== Способ решения == | == Способ решения == | ||
| - | Решение задачи производилось с помощью теоремы Фишера:<br> | + | Решение задачи производилось с помощью теоремы Фишера |
| + | На самом деле, проверка последовательности на "случайность" достаточно трудоемкая задача. В настоящее время используются десятки критериев для такой проверки. Вы можете ознакомиться более подробно с различными способами решения данной проблемы в книге Д. Кнут "Искусство программирования для ЭВМ. Том 2. Получисленные алгоритмы." <br> | ||
| + | Список критериев для проверки последовательности на "случайность":<br> | ||
| + | * [[Критерий хи-квадрат]] | ||
| + | * [[Критерий Колмогорова-Смирнова]] | ||
| + | * [[Критерий частот]] | ||
| + | * [[Критерий серий]] | ||
| + | * [[Критерий интервалов]] | ||
| + | * [[Покер-критерий]] | ||
| + | * [[Критерий собирания купонов]] | ||
| + | * [[Критерий перестановок]] | ||
| + | * [[Критерий монотонности]] | ||
| + | * [[Критерий "максимум-t"]] | ||
| + | * [[Критерий конфликтов]] | ||
| + | * [[Критерий промежутков между днями рождений]] | ||
| + | * [[Критерий сериальной корреляции]] | ||
| + | * [[Критерий подпоследовательностей]] | ||
| + | * [[Спектральный критерий]] | ||
| + | </ref> | ||
| + | :<br> | ||
<tex>X^{2}=\sum_{i=1}^{k}\frac{(n_{j}-E_{j})^{2}}{E_{j}}\sim\chi_{k-d-1}^{2}</tex>, где<br> | <tex>X^{2}=\sum_{i=1}^{k}\frac{(n_{j}-E_{j})^{2}}{E_{j}}\sim\chi_{k-d-1}^{2}</tex>, где<br> | ||
k = 10, - число различных чисел, учавствующих в эксперименте;<br> | k = 10, - число различных чисел, учавствующих в эксперименте;<br> | ||
| Строка 55: | Строка 74: | ||
Гипотеза H<sub>0</sub> о случайности называния принимается, | Гипотеза H<sub>0</sub> о случайности называния принимается, | ||
т.е. испытуемый один и два показали себя как хорошие генераторы случайных чисел. | т.е. испытуемый один и два показали себя как хорошие генераторы случайных чисел. | ||
| + | |||
== Смотри также == | == Смотри также == | ||
# [[Статистический анализ данных (курс лекций, К.В.Воронцов)/2008]] | # [[Статистический анализ данных (курс лекций, К.В.Воронцов)/2008]] | ||
[[Категория:Учебные задачи]] | [[Категория:Учебные задачи]] | ||
Версия 20:15, 11 января 2009
Содержание |
Постановка задачи
Человек называет числа от 1 до 10. Требуется проверить, является ли человек генератором случайных чисел, т.е. насколько такое называние случайно. Анализ названных чисел производить, не учитывая их последовательности в проведенном эксперименте.
Исходные данные
Проверяем гипотезу H0: называние случайно, т.е. человек - генератор случайных чисел. В эксперименте принимало участие 2 человека и компьютер. Первый и второй испытуемые называли числа вслух, экспериментатор производил запись чисел. Всего каждым испытуемым было названо 71 число. Затем на компьютере с помощью генератора случайных чисел также было сгенерировано 71 число. Данные эксперимента приведены ниже.
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Кол-Во | 7 | 9 | 9 | 4 | 10 | 5 | 7 | 8 | 6 | 6 |
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Кол-Во | 6 | 8 | 10 | 5 | 8 | 7 | 9 | 10 | 6 | 2 |
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Кол-Во | 4 | 5 | 6 | 9 | 14 | 8 | 6 | 8 | 5 | 6 |
Способ решения
Решение задачи производилось с помощью теоремы Фишера
На самом деле, проверка последовательности на "случайность" достаточно трудоемкая задача. В настоящее время используются десятки критериев для такой проверки. Вы можете ознакомиться более подробно с различными способами решения данной проблемы в книге Д. Кнут "Искусство программирования для ЭВМ. Том 2. Получисленные алгоритмы."
Список критериев для проверки последовательности на "случайность":
- Критерий хи-квадрат
- Критерий Колмогорова-Смирнова
- Критерий частот
- Критерий серий
- Критерий интервалов
- Покер-критерий
- Критерий собирания купонов
- Критерий перестановок
- Критерий монотонности
- Критерий "максимум-t"
- Критерий конфликтов
- Критерий промежутков между днями рождений
- Критерий сериальной корреляции
- Критерий подпоследовательностей
- Спектральный критерий
</ref>
, где
k = 10, - число различных чисел, учавствующих в эксперименте;
d = 0 , - число параметров, при определении вероятности успешного события;
nj , - сколько раз число j встретилось в проведенном эксперименте.
,
n = 71, - число событий в эксперименте;
pj = 1/10, - вероятность события встретиь число j в нашем эксперименте
Тогда для первого испытуемого:
Тогда для второго испытуемого:
Тогда для компьютера:
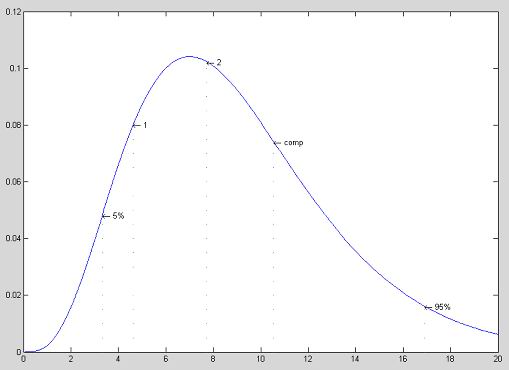
Гипотеза H0 о случайности называния принимается,
т.е. испытуемый один и два показали себя как хорошие генераторы случайных чисел.

