Метод Парзеновского окна (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 1: Строка 1:
'''Метод Парзеновского окна''' принадлежит к непараметрическим методам классификации и представляет собой одну из возможных реализаций байесовского подхода к решению задачи классификации.
'''Метод Парзеновского окна''' принадлежит к непараметрическим методам классификации и представляет собой одну из возможных реализаций байесовского подхода к решению задачи классификации.
== Постановка задачи разделения классов методом парзеновского окна ==
== Постановка задачи разделения классов методом парзеновского окна ==
-
Пусть у нас задана выборка <tex>\{(\mathbf{x}_i,y_i)\}_{i=1}^m</tex>, где <tex>X^m</tex> = <tex>\{\mathbf{x}_i\}_{i=1}^m</tex> - множество объектов, а <tex>Y^m</tex> = <tex>\{\mathbf{y}_i\}_{i=1}^m</tex> - множество<ref>Переписать.</ref> объектов на этих ответах. Кроме того, задан объект <tex>x_0</tex>, который небоходимо классифицировать.
+
Пусть у нас задана выборка <tex>\{(\mathbf{x}_i,y_i)\}_{i=1}^m</tex>, где <tex>X^m</tex> = <tex>\{\mathbf{x}_i\}_{i=1}^m</tex> - множество объектов, а <tex>Y^m</tex> = <tex>\{\mathbf{y}_i\}_{i=1}^m</tex> - множество ответов на этих объектах. Кроме того, задан объект <tex>x_0</tex>, который небоходимо классифицировать с помощью алгоритма <tex>a(x;X^{l},h)</tex>.
-
Задача состоит в том, что бы подобрать параметр <tex>h</tex> - ширину окна и тип ядра<ref>Ввести определение ядра и класс, из которого оно выбирается.</ref> таким образом,что бы при классификации с помощью метода парзеновского окна <ref>Переписать.</ref>ошибок было бы как можно меньше:
+
Задача состоит в том, что бы подобрать параметр <tex>h</tex>, ширину окна, и <tex>K</tex>ядерную функцию, таким образом, что бы при классификации с помощью метода парзеновского окна функционал качества достигал бы своего максимума при работе алгоритма с заданными параметрами:
-
<center><tex>a(x;X^{l},h)=\arg \max_{y\in Y} \lambda_{y} \sum_{i=1}^l {[}y_i = y{]} K\left(\frac{p(x,x_i)}{h}\right).</tex></center>
+
<center><tex>a(x;X^{l},h)=\arg \max_{y\in Y} \lambda_{y} \sum_{i=1}^l {[}y_i = y{]} K\left(\frac{\ro{}(x,x_i)}{h}\right).</tex></center>
 +
В этой формуле <tex>\lambda_{y}</tex> - цена правильного ответа для каждого класса из <tex>Y</tex>
 +
 
<ref>Описать все используемые переменные.</ref>
<ref>Описать все используемые переменные.</ref>
== Алгоритм отыскания оптимальных параметров ==
== Алгоритм отыскания оптимальных параметров ==
-
Для того, чтобы найти ширину окна и наиболее подходящий нам тип ядра, мы воспользуемся принципом максимального правдоподобия и исключением объектов по одному (leave-one-out,LOO):
+
Чтобы найти ширину окна и наиболее подходящий нам тип ядра, мы воспользуемся принципом максимального правдоподобия и исключением объектов по одному [[Скользящий контроль|leave-one-out]]:
-
<center><tex>h^{*}=\arg{ } \max_{h} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i) </tex></center>
+
<center><tex>h^{*}=\arg{ } \max_{h} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i). </tex></center>
-
То есть, мы будем восстанавливать значение класса для одного объекта из нашей выборки и максимизировать логарифм количества правильных ответов при исключении по очереди всех объектов выборки. Мы можем максимизоровать это значение по двум параметрам - ширине окна <tex>h</tex> и типу ядра. Ширину окна мы можем подобрать из некоторого диапазона, полученного из эмпирических предположений. Ядро можно выбрать из набора общеизвестных ядер. В моей работе рассматривались несколько основных типов ядер:
+
То есть, мы будем восстанавливать значение класса для одного объекта из нашей выборки и максимизировать логарифм количества правильных ответов при исключении по очереди всех объектов выборки. Максимизация этого значения происходит по двум параметрам - ширине окна <tex>h</tex> и типу ядерной функции. Ширину окна мы можем подобрать из некоторого диапазона <tex>\delta{}H</tex>, полученного из эмпирических предположений. Ядро выбирается из нижеприведенного набора ядер:
{| class="wikitable" style="text-align: center;"
{| class="wikitable" style="text-align: center;"
|- bgcolor="#cccccc"
|- bgcolor="#cccccc"
Строка 16: Строка 18:
! width=50 % |формула
! width=50 % |формула
|-
|-
-
| '''1''' || Епанечникова || <tex>E(r)=\frac{3}{4}(1-r^2){[}{|}r{|}<=1{]}</tex>
+
| '''1''' || Епанечникова || <tex>K_1(r)=E(r)=\frac{3}{4}(1-r^2){[}{|}r{|}<=1{]}</tex>
|-
|-
-
| '''2''' || Квартическое || <tex>Q(r)=\frac{15}{16}(1-r^2)^2{[}{|}r{|}<=1{]}</tex>
+
| '''2''' || Квартическое || <tex>K_2(r)=Q(r)=\frac{15}{16}(1-r^2)^2{[}{|}r{|}<=1{]}</tex>
|-
|-
-
| '''3''' || Треугольное || <tex>T(r)=(1-{|}r{|}){[}{|}r{|}<=1{]}</tex>
+
| '''3''' || Треугольное || <tex>K_3(r)=T(r)=(1-{|}r{|}){[}{|}r{|}<=1{]}</tex>
|-
|-
-
| '''4''' || Гауссовское || <tex>G(r)=(2\pi)^{(-\frac{1}{2})}exp(-\frac{1}{2}r^2)</tex>
+
| '''4''' || Гауссовское || <tex>K_4(r)=G(r)=(2\pi)^{(-\frac{1}{2})}exp(-\frac{1}{2}r^2)</tex>
|-
|-
-
| '''5''' || Прямоугольное || <tex>\Pi(r)=\frac{1}{2}{[}{|}r{|}<=1{]}</tex>
+
| '''5''' || Прямоугольное || <tex>K_5(r)=\Pi(r)=\frac{1}{2}{[}{|}r{|}<=1{]}</tex>
|-
|-
|}
|}
Получившееся выражение имеет достаточно понятный вид:
Получившееся выражение имеет достаточно понятный вид:
-
<center><tex>(h^{*},K(r))=\arg{ } \max_{K(r)} \max_{h} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i) </tex></center>
+
<center><tex>(h^{*},K^{*}_s(r))=\arg{ } \max_{s\in{{}1,2,3,4,5{}}} \max_{h\in\delta{}H} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i). </tex></center>
== Вычислительный эксперимент ==
== Вычислительный эксперимент ==
Строка 75: Строка 77:
== Исходный код ==
== Исходный код ==
-
Скачать листинги алгоритмов можно здесь [http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms/ParzenWindow/ parzenclassification.m, slidingcontrol.m, fqual.m, kgenerate.m]
+
Скачать листинги алгоритмов можно здесь [http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms/ParzenWindow/ parzenclassification.m, crossvalidation.m, fqual.m, kgenerate.m]
== Смотри также ==
== Смотри также ==
Строка 81: Строка 83:
* [[Метод ближайших соседей]]
* [[Метод ближайших соседей]]
* [[Многомерная случайная величина]]
* [[Многомерная случайная величина]]
 +
* [[Скользящий контроль]]
== Литература ==
== Литература ==
-
* К. В. Воронцов, Лекции по линейным алгоритмам классификации
+
# {{книга
 +
|автор = Воронцов К. В.
 +
|заглавие = Лекции по линейным алгоритмам классификации
 +
}}
 +
# {{книга
 +
|автор = Pascal Vincent and Yoshua Bengio
 +
|ссылка = http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.3.8792
 +
|заглавие = Manifold Parzen Windows
 +
|год = 2002
 +
}}
{{Задание|Зайцев Алексей|В.В. Стрижов|28 мая 2009}}
{{Задание|Зайцев Алексей|В.В. Стрижов|28 мая 2009}}

Версия 11:00, 24 мая 2009

Метод Парзеновского окна принадлежит к непараметрическим методам классификации и представляет собой одну из возможных реализаций байесовского подхода к решению задачи классификации.

Содержание

Постановка задачи разделения классов методом парзеновского окна

Пусть у нас задана выборка \{(\mathbf{x}_i,y_i)\}_{i=1}^m, где X^m = \{\mathbf{x}_i\}_{i=1}^m - множество объектов, а Y^m = \{\mathbf{y}_i\}_{i=1}^m - множество ответов на этих объектах. Кроме того, задан объект x_0, который небоходимо классифицировать с помощью алгоритма a(x;X^{l},h). Задача состоит в том, что бы подобрать параметр h, ширину окна, и Kядерную функцию, таким образом, что бы при классификации с помощью метода парзеновского окна функционал качества достигал бы своего максимума при работе алгоритма с заданными параметрами:

a(x;X^{l},h)=\arg \max_{y\in Y} \lambda_{y} \sum_{i=1}^l {[}y_i = y{]} K\left(\frac{\ro{}(x,x_i)}{h}\right).

В этой формуле \lambda_{y} - цена правильного ответа для каждого класса из Y

[1]

Алгоритм отыскания оптимальных параметров

Чтобы найти ширину окна и наиболее подходящий нам тип ядра, мы воспользуемся принципом максимального правдоподобия и исключением объектов по одному leave-one-out:

h^{*}=\arg{ } \max_{h} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i).

То есть, мы будем восстанавливать значение класса для одного объекта из нашей выборки и максимизировать логарифм количества правильных ответов при исключении по очереди всех объектов выборки. Максимизация этого значения происходит по двум параметрам - ширине окна h и типу ядерной функции. Ширину окна мы можем подобрать из некоторого диапазона \delta{}H, полученного из эмпирических предположений. Ядро выбирается из нижеприведенного набора ядер:

# ядро K(r) формула
1 Епанечникова K_1(r)=E(r)=\frac{3}{4}(1-r^2){[}{|}r{|}<=1{]}
2 Квартическое K_2(r)=Q(r)=\frac{15}{16}(1-r^2)^2{[}{|}r{|}<=1{]}
3 Треугольное K_3(r)=T(r)=(1-{|}r{|}){[}{|}r{|}<=1{]}
4 Гауссовское K_4(r)=G(r)=(2\pi)^{(-\frac{1}{2})}exp(-\frac{1}{2}r^2)
5 Прямоугольное K_5(r)=\Pi(r)=\frac{1}{2}{[}{|}r{|}<=1{]}

Получившееся выражение имеет достаточно понятный вид:

(h^{*},K^{*}_s(r))=\arg{ } \max_{s\in{{}1,2,3,4,5{}}} \max_{h\in\delta{}H} \sum_{i=1}^l \log \hat{p}_h (x_i;X^{m}{/}x_i).

Вычислительный эксперимент

Вычислительный эксперимент был проведен на реальных и модельных данных. В качестве модельных данных были взяты точки из двух нормальных распределений с разными математическими ожиданиями и дисперсиями (соответственно, были получены два класса объектов). После проведения рядка экспериментов были получены следующие результаты:

Код получения данных: 

%NORMGENERATION generation of normal data in 2 classes with different
%parameteres to be described in V: V(1,1) V(1,2) parameters of normal
%distribution for first class; V(2,1) V(2,2) parameters of normal
%distribution for first class; V(1,3) - number of properties; V(1,4),
%V(2,4) - number of objects in first and second class
X1=random('normal',V(1,1),V(1,2),V(1,3),V(1,4));
X2=random('normal',V(2,1),V(2,2),V(1,3),V(2,4));
X=[X1 , X2];
Y=[ones(1,V(1,4)) , zeros(1,V(2,4))];

В первом случае была использована такая матрица параметров распределения: 

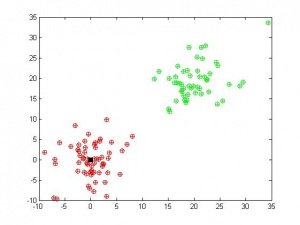
V=[0 4 2 60; 20 4 2 50]

Мы видим, что при хорошо разделимых классах, наш алгоритм работает замечательно при правильно подобранном значение k и любом ядре.

Матрица параметров распределения: 

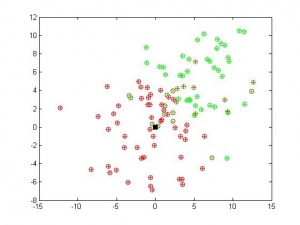
V=[0 4 2 60; 5 4 2 50]

Во втором случае классы были сближены, что привело к некоторому неустранимому числу ошибок.

Матрица параметров распределения: 

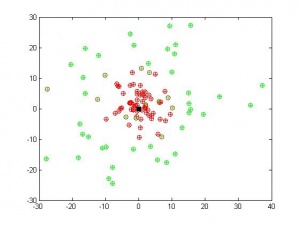
V=[0 4 2 60; 0 12 2 50]

В третьем случае были взяты два класса с одинаковыми математическими ожиданиями, но разными дисперсиями. Алгоритм достаточно хорошо разделил и их.

Исходный код

Скачать листинги алгоритмов можно здесь parzenclassification.m, crossvalidation.m, fqual.m, kgenerate.m

Смотри также

Литература

  1. Воронцов К. В. Лекции по линейным алгоритмам классификации.
  2. Pascal Vincent and Yoshua Bengio Manifold Parzen Windows. — 2002.


Данная статья является непроверенным учебным заданием.
Студент: Участник:Зайцев Алексей
Преподаватель: Участник:В.В. Стрижов
Срок: 28 мая 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Замечания

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%9F%D0%B0%D1%80%D0%B7%D0%B5%D0%BD%D0%BE%D0%B2%D1%81%D0%BA%D0%BE%D0%B3%D0%BE_%D0%BE%D0%BA%D0%BD%D0%B0_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты