Метод k взвешенных ближайших соседей (пример)
Материал из MachineLearning.
(Новая: {{TOCright}} <tex>K</tex> взвешенных ближайших соседей - это метрический алгоритм классификации, основанный на о...) |
|||
| Строка 28: | Строка 28: | ||
== Алгоритм отыскания оптимальных параметров == | == Алгоритм отыскания оптимальных параметров == | ||
Оптимальные значения параметров <tex>K</tex> и <tex>q</tex> определяют по критерию скользящего контроля с исключением объектов по одному: | Оптимальные значения параметров <tex>K</tex> и <tex>q</tex> определяют по критерию скользящего контроля с исключением объектов по одному: | ||
| - | <tex>(k^{*};q^{*}) = \arg{ } \max_{k,q}\ LOO(k;q;X^\ell\),</tex> где | + | <tex>(k^{*};q^{*}) = \arg{ } \max_{k,q}\ LOO(k;q;X^\ell\),</tex> где |
| + | <tex>LOO(k;q;X^\ell\)= \sum_{i=1}^{\l}\[y_i = a(x_i;X^{m}{\}x_i;k;q). </tex> | ||
| + | |||
| + | == Вычислительный эксперимент == | ||
| + | Показана работа алгоритма в серии задач, основанных как на реальных, так и на модельных данных. | ||
| + | |||
| + | === Пример 1 === | ||
| + | === Пример 2 === | ||
| + | |||
| + | === Пример на реальных данных: ирисы === | ||
| + | Проведена проверка алгоритма на классической задаче: [http://archive.ics.uci.edu/ml/datasets/Iris Ирисы Фишера] | ||
| + | Объектами являются три типа ирисов: [http://ru.wikipedia.org/wiki/%D0%98%D1%80%D0%B8%D1%81_%D1%89%D0%B5%D1%82%D0%B8%D0%BD%D0%B8%D1%81%D1%82%D1%8B%D0%B9 setosa], [http://en.wikipedia.org/wiki/Iris_versicolor versicolor], virginica | ||
| + | |||
| + | [[Изображение:setosa.jpg|275px]] | ||
| + | [[Изображение:versicolor.jpg|275px]] | ||
| + | [[Изображение:virginica.jpg|275px]] | ||
| + | |||
| + | У каждого объекта есть четыре признака: длина лепестка, ширина лепестка, длина чашелистика, ширина чашелистика. | ||
| + | Для удобства визуализации результатов будем использовать первые два признака. | ||
| + | В качестве обучающей и контрольной выборок выбрано по 25 представителей каждого из типов ирисов. | ||
| + | <source lang="matlab"> | ||
| + | %load data | ||
| + | load 'iris.txt'; | ||
| + | S = iris; | ||
| + | S(:,1:2) = []; %eliminating first two attributes | ||
| + | XL = S([1:25,51:75,101:125],:); | ||
| + | X = S([26:50,76:100,126:150],:); | ||
| + | YL = [ones([25,1]);2*ones([25,1]);3*ones([25,1])]; %creating class labels | ||
| + | Y = [ones([25,1]);2*ones([25,1]);3*ones([25,1])]; | ||
| + | |||
| + | %plotting data | ||
| + | plot(X(Y == 1,1),X(Y == 1,2),'*r'); | ||
| + | hold on | ||
| + | plot(X(Y == 2,1),X(Y == 2,2),'*b'); | ||
| + | plot(X(Y == 3,1),X(Y == 3,2),'*g'); | ||
| + | |||
| + | %getting classification | ||
| + | Y = makeWeightedKNN(XL, YL, X); | ||
| + | |||
| + | %plotting resulting classification | ||
| + | plot(X(Y == 1,1),X(Y == 1,2),'or'); | ||
| + | plot(X(Y == 2,1),X(Y == 2,2),'ob'); | ||
| + | plot(X(Y == 3,1),X(Y == 3,2),'og'); | ||
| + | title('Irises classification') | ||
| + | xlabel('petal width, cm'); | ||
| + | ylabel('petal length, cm'); | ||
| + | legend('Iris Setosa','Iris Versicolour','Iris Virginica','Location','NorthWest'); | ||
| + | hold off; | ||
| + | </source> | ||
| + | [[Изображение:Ireses_sorted.png|300px]] | ||
| + | |||
| + | Алгоритм хорошо классифицировал ирисы, допустив 4% ошибок. | ||
| + | |||
| + | == Исходный код == | ||
| + | |||
| + | == Смотри также == | ||
| + | |||
| + | == Литература == | ||
| + | |||
| + | {{Задание|Янович Юрий|В.В. Стрижов|28 мая 2009}} | ||
| + | |||
| + | == Замечания == | ||
Версия 22:25, 25 мая 2009
|
взвешенных ближайших соседей - это метрический алгоритм классификации, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.
Постановка задачи
Пусть - множество объектов;
- множество допустимых ответов. Задана обучающая выборка
. Задано множество объектов
.
Требуется найти найти множество ответов для объектов
.
Алгоритм 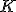 взвешенных ближайших соседей
взвешенных ближайших соседей
На множестве объектов задается евклидова функция расстояния
Для произвольного объекта расположим
объекты обучающей выборки
в порядке возрастания расстояний до
:
где через обозначается
тот объект обучающей выборки, который является
-м соседом объекта
.
Аналогичное обозначение введём и для ответа на
-м соседе:
.
Таким образом, произвольный объект порождает свою перенумерацию выборки.
В наиболее общем виде алгоритм ближайших соседей есть
где — заданная весовая функция,
которая оценивает степень важности
-го соседа для классификации объекта
.
В рассматриваемом примере что соответствует методу
экспоненциально взвешенных ближайших соседей, причем предполагается
.
Алгоритм отыскания оптимальных параметров
Оптимальные значения параметров и
определяют по критерию скользящего контроля с исключением объектов по одному:
где
Вычислительный эксперимент
Показана работа алгоритма в серии задач, основанных как на реальных, так и на модельных данных.
Пример 1
Пример 2
Пример на реальных данных: ирисы
Проведена проверка алгоритма на классической задаче: Ирисы Фишера Объектами являются три типа ирисов: setosa, versicolor, virginica
У каждого объекта есть четыре признака: длина лепестка, ширина лепестка, длина чашелистика, ширина чашелистика. Для удобства визуализации результатов будем использовать первые два признака. В качестве обучающей и контрольной выборок выбрано по 25 представителей каждого из типов ирисов.
%load data load 'iris.txt'; S = iris; S(:,1:2) = []; %eliminating first two attributes XL = S([1:25,51:75,101:125],:); X = S([26:50,76:100,126:150],:); YL = [ones([25,1]);2*ones([25,1]);3*ones([25,1])]; %creating class labels Y = [ones([25,1]);2*ones([25,1]);3*ones([25,1])]; %plotting data plot(X(Y == 1,1),X(Y == 1,2),'*r'); hold on plot(X(Y == 2,1),X(Y == 2,2),'*b'); plot(X(Y == 3,1),X(Y == 3,2),'*g'); %getting classification Y = makeWeightedKNN(XL, YL, X); %plotting resulting classification plot(X(Y == 1,1),X(Y == 1,2),'or'); plot(X(Y == 2,1),X(Y == 2,2),'ob'); plot(X(Y == 3,1),X(Y == 3,2),'og'); title('Irises classification') xlabel('petal width, cm'); ylabel('petal length, cm'); legend('Iris Setosa','Iris Versicolour','Iris Virginica','Location','NorthWest'); hold off;
Алгоритм хорошо классифицировал ирисы, допустив 4% ошибок.
Исходный код
Смотри также
Литература
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |




