Метод k ближайших соседей (пример)
Материал из MachineLearning.
м («Метод к ближайших соседей» переименована в «Метод k ближайших соседей (пример)») |
|||
| Строка 1: | Строка 1: | ||
| - | + | {{TOCright}} | |
| + | Метод <tex>K</tex> ближайших соседей - это [[Метрический классификатор|метрический алгоритм классификации]], основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты [[выборка|обучающей выборки]]. | ||
| + | |||
| + | == Постановка задачи == | ||
| + | Пусть <tex>X \in \mathbb{R}^n\</tex> - множество объектов; <tex>Y</tex> - множество допустимых ответов. Задана обучающая выборка <tex>\{(x_i,y_i)\}_{i=1}^\ell</tex>. Задано множество объектов <tex>\ X^m =\{x_i\}_{i=1}^m</tex>. | ||
| + | |||
| + | Требуется найти множество ответов <tex>\{y_i\}_{i=1}^m</tex> для объектов <tex>\{x_i\}_{i=1}^m</tex>. | ||
| + | |||
| + | == Алгоритм <tex>K</tex> ближайших соседей == | ||
| + | На множестве объектов задается некоторая функция расстояния, задаваемая пользовательской функцией <tex>\rho(x,x').</tex> Рассматривались следующие функции (ядра): евклидова | ||
| + | <center><tex>\rho(x,x') = \sum_{i=1}^n (x_i-x'_i)^2;</tex></center> | ||
| + | максимум модулей | ||
| + | <center><tex>\rho(x,x') = \max_{i} |x_i-x'_i|;</tex></center> | ||
| + | сумма модулей | ||
| + | <center><tex>\rho(x,x') = \sum_{i=1}^n |x_i-x'_i|.</tex></center> | ||
| + | |||
| + | Для произвольного объекта <tex>x\in X</tex> расположим | ||
| + | объекты обучающей выборки <tex>x_i</tex> в порядке возрастания расстояний до <tex>x</tex>: | ||
| + | ::<tex>\rho(x,x_{1; x}) \leq \rho(x,x_{2; x}) \leq \cdots \leq \rho(x,x_{m; x}),</tex> | ||
| + | где через <tex>x_{i; x}</tex> обозначается | ||
| + | тот объект обучающей выборки, который является <tex>i</tex>-м соседом объекта <tex>x</tex>. | ||
| + | Аналогичное обозначение введём и для ответа на <tex>i</tex>-м соседе: | ||
| + | <tex>y_{i; x}</tex>. | ||
| + | |||
| + | Таким образом, произвольный объект <tex>x</tex> порождает свою перенумерацию выборки. | ||
| + | В наиболее общем виде [[алгоритм]] ближайших соседей есть | ||
| + | ::<tex>a(x) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ x_{i; x}=y \bigr] w(i,x),</tex> | ||
| + | где <tex>w(i,x)</tex> — заданная ''весовая функция'', | ||
| + | которая оценивает степень важности <tex>i</tex>-го соседа для классификации объекта <tex>u</tex>. | ||
| + | |||
| + | В рассматриваемом примере <tex>w(i,x) = [i\leq k] ,</tex> что соответствует методу <tex>k</tex> ближайших соседей. | ||
| + | |||
| + | === Алгоритм отыскания оптимальных параметров === | ||
| + | Оптимальные значения параметра <tex>K</tex> определяют по критерию скользящего контроля с исключением объектов по одному: | ||
| + | <tex>(k^{*}) = \arg{ } \max_{k}\ LOO(k;X^\ell\),</tex> где | ||
| + | <tex>LOO(k;X^\ell\)= \sum_{i=1}^l\[y_i = a(x_i;X^l \setminus x_i;k)]. </tex> | ||
| + | |||
| + | == Вычислительный эксперимент == | ||
| + | Показана работа алгоритма в серии задач, основанных как на реальных, так и на модельных данных. | ||
| + | |||
| + | === Пример 1 === | ||
| + | Рассмотрим пример на модельных данных. Выборка состоит из трех классов, которые являются гауссовскими рапределением с диагональными матрицами ковариации. | ||
| + | <source lang="matlab"> | ||
| + | function demo_KMeans() | ||
| + | %% Set parameters | ||
| + | %generating 3 sample normal classes | ||
| + | N = 100; | ||
| + | % 1st class contains N objects | ||
| + | alpha = 1.5; % 2nd class contains alpha*N ones | ||
| + | sig2 = 1; % assume 2nd class has the same variance as the 1st | ||
| + | dist2 = 4; % distance from the 1st class | ||
| + | |||
| + | % parameters for the 3rd class | ||
| + | beta = 1.3; | ||
| + | sig3 = 1.5; | ||
| + | dist3 = 3; | ||
| + | % | ||
| + | % % later we move this piece of code in a separate file | ||
| + | % X - coordinates of educational sequence | ||
| + | % y - classes of elements in educatioanal sequence | ||
| + | [X, y] = loadModelData3(N, alpha, sig2, dist2, beta, sig3, dist3); | ||
| + | |||
| + | %% Section title | ||
| + | % | ||
| + | % idx* - indexes of class * in X | ||
| + | idx1 = find(y == 0); % object indices for the 1st class | ||
| + | idx2 = find(y == 1); | ||
| + | idx3 = find(y == 2); | ||
| + | |||
| + | minErrors=0; | ||
| + | %% Main calculations | ||
| + | funcNorm = 'normEuc'; | ||
| + | CalcAndPlot('normEuc', X, y, idx1,idx2,idx3) | ||
| + | |||
| + | funcNorm = 'normMax'; | ||
| + | CalcAndPlot('normMax', X, y, idx1,idx2,idx3) | ||
| + | |||
| + | funcNorm = 'normAbs'; | ||
| + | CalcAndPlot('normAbs', X, y, idx1,idx2,idx3) | ||
| + | |||
| + | end | ||
| + | |||
| + | function CalcAndPlot(funcNorm, X, y, idx1,idx2,idx3) | ||
| + | % RR - indexes of ordered educ. seq. | ||
| + | RR=GetBigIndices4(X, funcNorm); | ||
| + | % Kopt - optimal parameter for method | ||
| + | [Kopt,minErrors] = GetK3(RR,y) | ||
| + | % draw results: | ||
| + | |||
| + | PlotClassification4(X,y,Kopt,idx1,idx2,idx3, funcNorm,minErrors) | ||
| + | end | ||
| + | </source> | ||
| + | |||
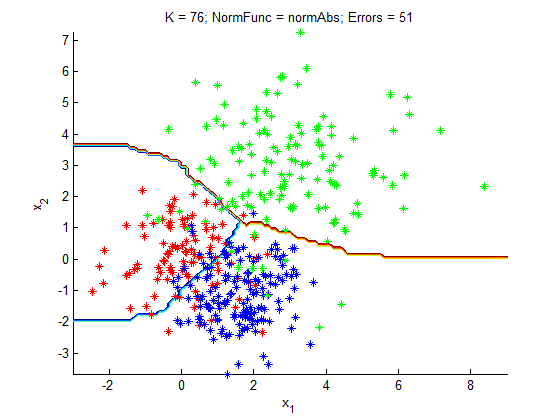
| + | [[Изображение:KNN_ex.png|800px]] | ||
| + | |||
| + | |||
| + | На графике по осям отложены величины признаков объектов, различные классы показаны крестиками различных цветов, а результат классификации показан разделительными линиями различных цветов. | ||
| + | |||
| + | === Пример на реальных данных: ирисы === | ||
| + | Проведем проверку алгоритма на классической задаче: [http://archive.ics.uci.edu/ml/datasets/Iris Ирисы Фишера] | ||
| + | Объектами являются три типа ирисов: [http://ru.wikipedia.org/wiki/%D0%98%D1%80%D0%B8%D1%81_%D1%89%D0%B5%D1%82%D0%B8%D0%BD%D0%B8%D1%81%D1%82%D1%8B%D0%B9 setosa], [http://en.wikipedia.org/wiki/Iris_versicolor versicolor], [http://en.wikipedia.org/wiki/Claytonia_virginica virginica] | ||
| + | |||
| + | [[Изображение:setosa.jpg|275px]] | ||
| + | [[Изображение:versicolor.jpg|275px]] | ||
| + | [[Изображение:virginica.jpg|275px]] | ||
| + | |||
| + | У каждого объекта есть четыре признака: длина лепестка, ширина лепестка, длина чашелистика, ширина чашелистика. | ||
| + | Для удобства визуализации результатов будем использовать первые два признака. | ||
| + | В качестве обучающей и контрольной выборок выбрано по 25 представителей каждого из типов ирисов. | ||
| + | <source lang="matlab"> | ||
| + | function xxx = PlotIris() | ||
| + | load 'iris.txt' | ||
| + | X = iris; | ||
| + | y=[zeros(50,1);ones(50,1);2*ones(50,1)]; | ||
| + | idx1 = find(y == 0); % object indices for the 1st class | ||
| + | idx2 = find(y == 1); | ||
| + | idx3 = find(y == 2); | ||
| + | CalcAndPlot('normEuc', X, y, idx1,idx2,idx3) | ||
| + | |||
| + | CalcAndPlot('normMax', X, y, idx1,idx2,idx3) | ||
| + | |||
| + | CalcAndPlot('normAbs', X, y, idx1,idx2,idx3) | ||
| + | |||
| + | end | ||
| + | |||
| + | function CalcAndPlot(funcNorm, X, y, idx1,idx2,idx3) | ||
| + | % RR - indexes of ordered educ. seq. | ||
| + | RR=GetBigIndices4(X, funcNorm); | ||
| + | % Kopt - optimal parameter for method | ||
| + | [Kopt,minErrors] = GetK3(RR,y) | ||
| + | % draw results: | ||
| + | |||
| + | PlotClassification4(X,y,Kopt,idx1,idx2,idx3, funcNorm,minErrors) | ||
| + | end | ||
| + | |||
| + | </source> | ||
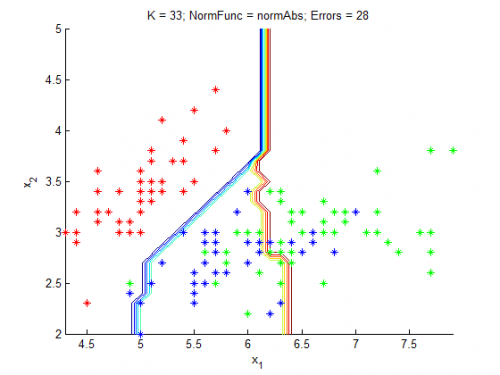
| + | [[Изображение:Irisx.png|500px]] | ||
| + | |||
| + | На графике различные классы показаны крестиками различных цветов, а результат классификации показан разделительными линиями различных цветов. Алгоритм хорошо классифицировал ирисы. | ||
| + | |||
| + | == Исходный код == | ||
| + | Скачать листинги алгоритмов можно здесь [http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms/KMeansFunc/ ]. | ||
| + | |||
| + | == Смотри также == | ||
| + | * [[Метрический классификатор]] | ||
| + | * [[Метод ближайших соседей]] | ||
| + | * [[Скользящий контроль]] | ||
| + | |||
| + | == Литература == | ||
| + | * К. В. Воронцов, Лекции по метрическим алгоритмам классификации | ||
| + | * Bishop C. - Pattern Recognition and Machine Learning. Springer. 2006. | ||
| + | * Abidin, T. and Perrizo, W. SMART-TV: A Fast and Scalable Nearest Neighbor Based Classifier for Data Mining. Proceedings of ACM SAC-06, Dijon, France, April 23-27, 2006. ACM Press, New York, NY, pp.536-540 | ||
| + | * Wang, H. and Bell, D. Extended k-Nearest Neighbours Based on Evidence Theory. The Computer Journal, Vol. 47 (6) Nov. 2004, pp. 662-672. | ||
| + | * Yu, K. and Ji, L. Karyotyping of Comparative Genomic Hybridization Human Metaphases Using Kernel Nearest-Neighbor Algorithm, Cytometry 2002. | ||
| + | * Domeniconi, C., and Yan, B. On Error Correlation and Accuracy of Nearest Neighbor Ensemble Classifiers. Proceedings of the SIAM International Conference on Data Mining, Newport Beach, California, April 21-23, 2005 | ||
| + | * UCI Machine Learning Repository, available on line at the University of California,Irvine http://www.ics.uci.edu/~mlearn/MLSum mary.html | ||
| + | {{Задание|Литвинов Игорь|В.В. Стрижов|16 июня 2009}} | ||
Версия 20:47, 19 июня 2009
|
Метод ближайших соседей - это метрический алгоритм классификации, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.
Постановка задачи
Пусть - множество объектов;
- множество допустимых ответов. Задана обучающая выборка
. Задано множество объектов
.
Требуется найти множество ответов для объектов
.
Алгоритм 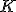 ближайших соседей
ближайших соседей
На множестве объектов задается некоторая функция расстояния, задаваемая пользовательской функцией Рассматривались следующие функции (ядра): евклидова
максимум модулей
сумма модулей
Для произвольного объекта расположим
объекты обучающей выборки
в порядке возрастания расстояний до
:
где через обозначается
тот объект обучающей выборки, который является
-м соседом объекта
.
Аналогичное обозначение введём и для ответа на
-м соседе:
.
Таким образом, произвольный объект порождает свою перенумерацию выборки.
В наиболее общем виде алгоритм ближайших соседей есть
где — заданная весовая функция,
которая оценивает степень важности
-го соседа для классификации объекта
.
В рассматриваемом примере что соответствует методу
ближайших соседей.
Алгоритм отыскания оптимальных параметров
Оптимальные значения параметра определяют по критерию скользящего контроля с исключением объектов по одному:
где
Вычислительный эксперимент
Показана работа алгоритма в серии задач, основанных как на реальных, так и на модельных данных.
Пример 1
Рассмотрим пример на модельных данных. Выборка состоит из трех классов, которые являются гауссовскими рапределением с диагональными матрицами ковариации.
function demo_KMeans() %% Set parameters %generating 3 sample normal classes N = 100; % 1st class contains N objects alpha = 1.5; % 2nd class contains alpha*N ones sig2 = 1; % assume 2nd class has the same variance as the 1st dist2 = 4; % distance from the 1st class % parameters for the 3rd class beta = 1.3; sig3 = 1.5; dist3 = 3; % % % later we move this piece of code in a separate file % X - coordinates of educational sequence % y - classes of elements in educatioanal sequence [X, y] = loadModelData3(N, alpha, sig2, dist2, beta, sig3, dist3); %% Section title % % idx* - indexes of class * in X idx1 = find(y == 0); % object indices for the 1st class idx2 = find(y == 1); idx3 = find(y == 2); minErrors=0; %% Main calculations funcNorm = 'normEuc'; CalcAndPlot('normEuc', X, y, idx1,idx2,idx3) funcNorm = 'normMax'; CalcAndPlot('normMax', X, y, idx1,idx2,idx3) funcNorm = 'normAbs'; CalcAndPlot('normAbs', X, y, idx1,idx2,idx3) end function CalcAndPlot(funcNorm, X, y, idx1,idx2,idx3) % RR - indexes of ordered educ. seq. RR=GetBigIndices4(X, funcNorm); % Kopt - optimal parameter for method [Kopt,minErrors] = GetK3(RR,y) % draw results: PlotClassification4(X,y,Kopt,idx1,idx2,idx3, funcNorm,minErrors) end
На графике по осям отложены величины признаков объектов, различные классы показаны крестиками различных цветов, а результат классификации показан разделительными линиями различных цветов.
Пример на реальных данных: ирисы
Проведем проверку алгоритма на классической задаче: Ирисы Фишера Объектами являются три типа ирисов: setosa, versicolor, virginica
У каждого объекта есть четыре признака: длина лепестка, ширина лепестка, длина чашелистика, ширина чашелистика. Для удобства визуализации результатов будем использовать первые два признака. В качестве обучающей и контрольной выборок выбрано по 25 представителей каждого из типов ирисов.
function xxx = PlotIris() load 'iris.txt' X = iris; y=[zeros(50,1);ones(50,1);2*ones(50,1)]; idx1 = find(y == 0); % object indices for the 1st class idx2 = find(y == 1); idx3 = find(y == 2); CalcAndPlot('normEuc', X, y, idx1,idx2,idx3) CalcAndPlot('normMax', X, y, idx1,idx2,idx3) CalcAndPlot('normAbs', X, y, idx1,idx2,idx3) end function CalcAndPlot(funcNorm, X, y, idx1,idx2,idx3) % RR - indexes of ordered educ. seq. RR=GetBigIndices4(X, funcNorm); % Kopt - optimal parameter for method [Kopt,minErrors] = GetK3(RR,y) % draw results: PlotClassification4(X,y,Kopt,idx1,idx2,idx3, funcNorm,minErrors) end
На графике различные классы показаны крестиками различных цветов, а результат классификации показан разделительными линиями различных цветов. Алгоритм хорошо классифицировал ирисы.
Исходный код
Скачать листинги алгоритмов можно здесь [1].
Смотри также
Литература
- К. В. Воронцов, Лекции по метрическим алгоритмам классификации
- Bishop C. - Pattern Recognition and Machine Learning. Springer. 2006.
- Abidin, T. and Perrizo, W. SMART-TV: A Fast and Scalable Nearest Neighbor Based Classifier for Data Mining. Proceedings of ACM SAC-06, Dijon, France, April 23-27, 2006. ACM Press, New York, NY, pp.536-540
- Wang, H. and Bell, D. Extended k-Nearest Neighbours Based on Evidence Theory. The Computer Journal, Vol. 47 (6) Nov. 2004, pp. 662-672.
- Yu, K. and Ji, L. Karyotyping of Comparative Genomic Hybridization Human Metaphases Using Kernel Nearest-Neighbor Algorithm, Cytometry 2002.
- Domeniconi, C., and Yan, B. On Error Correlation and Accuracy of Nearest Neighbor Ensemble Classifiers. Proceedings of the SIAM International Conference on Data Mining, Newport Beach, California, April 21-23, 2005
- UCI Machine Learning Repository, available on line at the University of California,Irvine http://www.ics.uci.edu/~mlearn/MLSum mary.html
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |