Выбор признаков с помощью генетических алгоритмов (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Результаты на реальных данных)
(→Исходный код)
 
(50 промежуточных версий не показаны.)
Строка 5: Строка 5:
Задана выборка&nbsp;&#151; множество <tex>\{x_1,...,x_n|x_i\in\mathbb{R}^M\}</tex> значений свободных
Задана выборка&nbsp;&#151; множество <tex>\{x_1,...,x_n|x_i\in\mathbb{R}^M\}</tex> значений свободных
переменных и множество <tex>\{y_1,...,y_n| y_i\in\mathbb{R}\}</tex> соответствующих им значений зависимой переменной.
переменных и множество <tex>\{y_1,...,y_n| y_i\in\mathbb{R}\}</tex> соответствующих им значений зависимой переменной.
-
Задано множество порождающих функций линейной регрессионной модели <tex>\{\mathbf{f}_1,...,\mathbf{f}_N\}</tex>, где <tex>\mathbf{f}_i:\: \mathbb{R}^M \to \mathbb{R}</tex>. Введем обозначения: <br />
+
Задано множество порождающих функций линейной регрессионной модели <tex>\{\mathbf{f}_1,...,\mathbf{f}_N\},</tex> где <tex>\mathbf{f}_i:\: \mathbb{R}^M \to \mathbb{R}</tex>. Введем обозначения: <br />
-
<tex>c\in\{0,1\}^N</tex>,
+
<tex>c\in\{0,1\}^N,</tex>
-
<tex>F(c) =\left(\begin{array}{ccc} \mathbf{f}_{i_1}(x_1) & \ldots & \mathbf{f}_{i_k}(x_1)\\ \mathbf{f}_{i_1}(x_2) & \ldots & \mathbf{f}_{i_k}(x_2)\\ \ldots & \ldots & \ldots \\ \mathbf{f}_{i_1}(x_n) & \ldots & \mathbf{f}_{i_k}(x_n)\\ \end{array} \right) </tex>, k = ||c||<sub>1</sub>, {&nbsp;i<sub>j</sub>&nbsp;}<sub>j=1</sub><sup>k</sup>⊂{ 1,...,N } : c( i<sub>j</sub> )=1 при j=1,...,k; <br />
+
<tex>F(c) =\left(\begin{array}{ccc} \mathbf{f}_{i_1}(x_1) & \ldots & \mathbf{f}_{i_k}(x_1)\\ \mathbf{f}_{i_1}(x_2) & \ldots & \mathbf{f}_{i_k}(x_2)\\ \ldots & \ldots & \ldots \\ \mathbf{f}_{i_1}(x_n) & \ldots & \mathbf{f}_{i_k}(x_n)\\ \end{array} \right), </tex> <tex>k = ||c||_1,\; {\{i_j\}_{j=1}}^k \subset \{ 1,...,N \}\;: \; c(i_j)=1</tex> при <tex>j=1,...,k;</tex> <br />
<tex>\mathbf{w(c)} = (F(c)^TF(c))^{-1}F(c)^T\mathbf{y};</tex> <br />
<tex>\mathbf{w(c)} = (F(c)^TF(c))^{-1}F(c)^T\mathbf{y};</tex> <br />
<tex>\mathbf{y(c)} = F(c)\mathbf{w(c)}.</tex> <br />
<tex>\mathbf{y(c)} = F(c)\mathbf{w(c)}.</tex> <br />
Строка 14: Строка 14:
== Описание алгоритма ==
== Описание алгоритма ==
-
Свободные параметры: размер популяции, доля кроссоверинга ( доля особей одного поколения, подвергающихся кроссоверингу ).
+
Свободные параметры: размер популяции, доля кроссинговера (доля особей одного поколения, подвергающихся кроссинговеру).
-
#Инициализация( создание начальной популяции необходимого размера ). Хромосомы особей представляют собой битовые векторы со случайными компонентами. Счетчик числа итераций: n=0.
+
#Инициализация (создание начальной популяции необходимого размера). Хромосомы особей представляют собой битовые векторы со случайными компонентами. Счетчик числа итераций: <tex>n:=0.</tex>
-
#n:=n+1. Проверка условий завершения: либо n превысило максимально допустимое значение, либо изменения целевой функции SSE для лучшей особи в популяции за некоторое число итераций оказалось слишком малым.
+
#<tex>n:=n+1.</tex> Проверка условий завершения: либо <tex>n</tex> превысило максимально допустимое значение, либо изменения целевой функции SSE для лучшей особи в популяции за некоторое число итераций оказалось слишком малым.
-
#Селекция( выбор особей для следующего поколения ). Селекция выполняется на основе оценки SSE всех особей. Используемый механизм таков: на единичном отрезке каждой особи выделяется участок, длина которого пропорциональна SSE. Далее алгоритм-селектор движется вдоль отрезка с фиксированным шагом, выбирая каждый раз ту особь, над которой находится. Начальная точка выбирается случайно, при этом начальное расстояние до левого конца должно быть меньше шага.
+
#Селекция (выбор особей для следующего поколения). Селекция выполняется на основе оценки SSE всех особей. Используемый механизм таков: на единичном отрезке каждой особи выделяется участок, длина которого пропорциональна SSE. Далее алгоритм-селектор движется вдоль отрезка с фиксированным шагом, выбирая каждый раз ту особь, над которой находится. Начальная точка выбирается случайно, при этом начальное расстояние до левого конца должно быть меньше шага.
-
#Кроссоверинг. Выбирается число особей, равное доли кроссоверинга * размер популяции. С парами особей выполняется так называемый кроссоверинг с маской( см. [[Генетический алгоритм|Оператор скрещивания]] ). В результате этой операции каждая аллель ( т. е. позиция в хромосоме особи ) случайным образом заполняется геном 1-ого или 2-ого родителя.
+
#Кроссинговер. Выбирается число особей, равное доли кроссинговера * размер популяции. С парами особей выполняется так называемый кроссинговер с маской (см. [[Генетический алгоритм|Оператор скрещивания]]). В результате этой операции каждая аллель (т. е. позиция в хромосоме особи) случайным образом заполняется геном 1-ого или 2-ого родителя.
-
#Мутация. Для каждой особи в каждой аллели с вероятностью 0.01 происходит мутация, которая выражается в замене текущего гена на 0 или 1 случайным образом( равновероятно ).
+
#Мутация. Для каждой особи в каждой аллели с вероятностью 0.01 происходит мутация, которая выражается в замене текущего гена на 0 или 1 случайным образом (равновероятно).
#Возвращение на шаг 2.
#Возвращение на шаг 2.
 +
=== Замечание ===
 +
Существует еще одна модификация оператора кроссинговера - одноточечная, когда случайным образом выбирается позиция в хромосоме, и хромосомы особей обмениваются подстроками, заключенными между этой позицией и правым концом строки (см. [[Генетический алгоритм|Оператор скрещивания]]). Для этой модификации справедлива [[теорема схемы]], которая имеет наглядную интерпретацию в терминах рассматриваемой задачи. Кратко изложим основную идею. <br />
 +
Пусть имеется какая-то начальная популяция. Рассмотрим некоторую совокупность признаков, не очень большую и имеющую не очень большое расстояние между крайними левыми и правыми позициями в хромосоме, дающую приближение в смысле SSE лучше, чем в среднем по данной популяции. Тогда количество появлений такой совокупности признаков в последующих популяциях будет расти экспоненциально на протяжении некоторого числа популяций. Таким образом, наборы признаков с высоким качеством сохраняются и распространяются по популяции. <br />
 +
Однако в данном исследовании используется кроссинговер с маской, для которого теорема схемы формально не может применяться.
== Вычислительный эксперимент ==
== Вычислительный эксперимент ==
Строка 26: Строка 30:
=== Модельные данные ===
=== Модельные данные ===
-
Данные порождались следующим образом:
+
Данные порождались следующим образом (D - дисперсия):
<source lang="matlab">
<source lang="matlab">
x = [ 1:0.5:20 ]';
x = [ 1:0.5:20 ]';
-
y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + randn( size( x, 1 ), 1 );
+
y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + sqrt( D ) * randn( size( x, 1 ), 1 );
</source>
</source>
-
Выборка делилась на training и testing части в соотношении 60%:40% случайным образом. Исследовались 2 эффекта: ложная ( ранняя ) сходимость и переобучение.
+
Выборка делилась на training и testing части в соотношении 60%:40% случайным образом. Исследовались 2 эффекта: ложная (ранняя) сходимость и переобучение.
 +
 
=== Результаты на модельных данных ===
=== Результаты на модельных данных ===
-
Использовался следующий набор порождающих функций ( всего 12 ): <br />
+
Использовался следующий набор порождающих функций (всего 12): <br />
<tex>1,\; x,\; x^2,\; log(x),\; x^3,\; x*log(x),\; x^4,\; x^2*log(x),\; x^2*cos(x),\; cos(x)*log(x),\; x*sin(x)*log(x),\; x^2*cos(x)*log(x).</tex> <br />
<tex>1,\; x,\; x^2,\; log(x),\; x^3,\; x*log(x),\; x^4,\; x^2*log(x),\; x^2*cos(x),\; cos(x)*log(x),\; x*sin(x)*log(x),\; x^2*cos(x)*log(x).</tex> <br />
В наборе не было следующих функций, участвовавших в порождении: <tex>sin(x),\; x^2*sin(x).</tex>
В наборе не было следующих функций, участвовавших в порождении: <tex>sin(x),\; x^2*sin(x).</tex>
-
[[Изображение:SSE( number of generations ) for varyingPopulationSize.png|1000px]] <br />
+
==== Случай небольшой дисперсии (D=1) ====
-
График training,5 демонстрирует раннюю сходимость. Графики 10 демонстрируют раннюю сходимость + переобучение. Графики 15 показывают сходимость без переобучения. <br />
+
[[Изображение:SSE( number of generations ) for varyingPopulationSizeN.png|600px]] <br />
-
[[Изображение:Number of Iterations(PopulationSize).png|800px]] <br />
+
График для размера популяции 5 демонстрирует раннюю сходимость на обучающем множестве (training,5). Графики для размера популяции 10 демонстрируют раннюю сходимость и переобучение (т.е. SSE мало на обучающем множестве и велико на контрольном). Графики для размера популяции 15 показывают сходимость без переобучения. <br />
-
Подтверждение ранней сходимости для случаев 5, 10. Дольше всех работает 15. <br />
+
[[Изображение:Number of Iterations(PopulationSize).png|600px]] <br />
-
[[Изображение:Least squares linear fit for varyingPopulationSize.png|1000px]] <br />
+
Подтверждение ранней сходимости для размеров популяции 5, 10. Дольше всего алгоритм работает для значения 15. <br />
-
Наглядная демонстрация ранней сходимости и переобучения. В случаях 5, 10 выборка хорошо приближена на training-части, а на test-части наблюдаются сильные отклонения. Для случая 15 - подтверждается отсутствие ранней сходимости, переобучения. <br />
+
[[Изображение:Least squares linear fit for varyingPopulationSize.png|600px]] <br />
-
[[Изображение:SSE( number of generations ) for varyingCrossoverFraction.png|1000px]] <br />
+
Наглядная демонстрация ранней сходимости и переобучения. Для размеров популяции 5, 10 SSE мало на training-части и велико на test-части. Для размера популяции 15 - подтверждается отсутствие ранней сходимости, переобучения. <br />
-
Случаи 0.3, 0.7 характеризуются явным переобучением. Для случая 0.5 переобучение не наблюдается, только незначительная ранняя сходимость. <br />
+
[[Изображение:SSE( number of generations ) for varyingCrossoverFraction.png|600px]] <br />
-
[[Изображение:Number of Iterations(CrossoverFraction).png|800px]] <br />
+
Графики для долей кроссинговера 0.3, 0.7 характеризуются переобучением. Для доли кроссинговера 0.5 переобучение не наблюдается, только ранняя сходимость. <br />
-
[[Изображение:Least squares linear fit for varyingCrossoverFraction.png|1000px]] <br />
+
[[Изображение:Number of Iterations(CrossoverFraction).png|600px]] <br />
-
Наглядная демонстрация переобучения для случаев 0.3, 0.7. В случае 0.5 нет явного переобучения, как уже было замечено ранее.
+
[[Изображение:Least squares linear fit for varyingCrossoverFraction.png|600px]] <br />
 +
Наглядная демонстрация переобучения для долей кроссинговера 0.3, 0.7. Для значения 0.5 нет явного переобучения, как уже было замечено ранее.
 +
===== Выводы =====
 +
Чем больше размер популяции, тем менее вероятно переобучение и ранняя сходимость. Оптимальное значение доли кроссинговера равно 0.5.
-
=== Выводы ===
+
==== Случай значительной дисперсии (D=160000) ====
-
Чем больше размер популяции, тем менее вероятно переобучение и ранняя сходимость. Оптимальное значение доли кроссоверинга равно 0.5.
+
[[Изображение:SSE( number of generations ) for varyingPopulationSize( huge disp )N.png|600px]] <br />
 +
Видно, что для размера популяции 5 результатом работы алгоритма является точка пространства поиска с SSE значительно большим, чем для размеров популяции 10, 15. <br />
 +
[[Изображение:SSE( number of generations ) for varyingCrossoverFraction( huge disp )N.png|600px]] <br />
 +
Начиная с 36-ой итерации все графики сливаются. <br />
 +
[[Изображение:Least squares linear fit for varyingPopulationSize( huge disp )N.png|600px]] <br />
 +
Четко видно отклонение синей линии, соответствующей размеру популяции 5, от линий, соответствующих значениям 10, 15 (эти линии сливаются). Графики SSE для всех значений, приведенные ранее, показали, что SSE для итоговой точки при значении 5 больше SSE в случаях 10, 15. <br />
 +
[[Изображение:Least squares linear fit for varyingCrossoverFraction( huge disp )N.png|600px]] <br />
 +
Все 3 графика сливаются, как уже было замечено ранее. <br />
 +
===== Выводы =====
 +
При значительном шуме зависимость эффективности от доли кроссинговера очень слабая. Однако зависимость от размера популяции по-прежнему заметна, чем больше значение этого параметра - тем лучше.
=== Реальные данные ===
=== Реальные данные ===
Выборка с улыбкой волатильности. 2 независимые переменные: время и страйк, зависимая переменная - волатильность. Выборка делилась как и прежде.
Выборка с улыбкой волатильности. 2 независимые переменные: время и страйк, зависимая переменная - волатильность. Выборка делилась как и прежде.
=== Результаты на реальных данных ===
=== Результаты на реальных данных ===
-
Использовался следующий набор порождающих функций ( всего 21 ): <br />
+
Использовался следующий набор порождающих функций (всего 26): <br />
<tex>1,\; x(1),\; x(1)^2,\; x(1)^3,\; x(1)^4,\; x(2),\; x(2)^2,\; x(2)^3,\; x(2)^4,\; sin(x(1)),\; sin(x(2)),\; x(1)*x(2),\; x(1)*x(2)^2,\; x(1)*x(2)^3,\; x(1)*x(2)^4,</tex> <br />
<tex>1,\; x(1),\; x(1)^2,\; x(1)^3,\; x(1)^4,\; x(2),\; x(2)^2,\; x(2)^3,\; x(2)^4,\; sin(x(1)),\; sin(x(2)),\; x(1)*x(2),\; x(1)*x(2)^2,\; x(1)*x(2)^3,\; x(1)*x(2)^4,</tex> <br />
-
<tex>x(1)^2*x(2),\; x(1)^2*x(2)^2,\; sin(x(1))*x(2),\; sin(x(1))*x(2)^2,\; sin(x(2))*x(1),\; sin(x(2))*x(1)^2.</tex> <br />
+
<tex>x(1)^2*x(2),\; x(1)^2*x(2)^2,\; sin(x(1))*x(2),\; sin(x(1))*x(2)^2,\; sin(x(2))*x(1),\; sin(x(2))*x(1)^2,\; 1/(x(1)+0.1),\; 1/(x(2)+0.1),</tex> <br />
-
[[Изображение:Sample.png|1000px]] <br />
+
<tex>log(0.1+x(1)),\; log(0.1+x(2)),\; exp(x(1)).</tex> <br />
-
[[Изображение:SSE( number of generations ) for varyingPopulationSize2D.png|1000px]] <br />
+
[[Изображение:Sample.png|800px]] <br />
-
Случай 10 явно демонстрирует переобучение. Самый лучший результат - в случае 15. <br />
+
[[Изображение:SSE( number of generations ) for varyingPopulationSize2D!.png|600px]] <br />
-
[[Изображение:Least squares linear fit, varyingPopulationSize(value1).png|1000px]] <br />
+
Результат с наименьшим SSE - при размере популяции 15, с наибольшим SSE - при размере популяции 5. <br />
-
Нормальный результат, но это скорее случайность. График SSE показал, что алгоритм почти сразу случайно попал в минимум.
+
[[Изображение:Least squares linear fit, varyingPopulationSize(value1)!.png|600px]] <br />
-
[[Изображение:Least squares linear fit, varyingPopulationSize(value2).png|1000px]] <br />
+
Результат с наибольшим SSE. Никакого сходства с данными. <br />
-
Переобучение: красный правый угол поверхности "загнут" не в ту сторону. <br />
+
[[Изображение:Least squares linear fit, varyingPopulationSize(value2)!.png|600px]] <br />
-
[[Изображение:Least squares linear fit, varyingPopulationSize(value3).png|1000px]] <br />
+
Неплохой результат, но видно, что красный край недостаточно загнут вверх относительно исходных данных, что выражается в большом значении SSE по сравнению с результатом для размера популяции 15. <br />
-
Самый лучший результат. <br />
+
[[Изображение:Least squares linear fit, varyingPopulationSize(value3)!.png|600px]] <br />
-
[[Изображение:SSE( number of generations ) for varyingCrossoverFraction2D.png|1000px]] <br />
+
Результат с наименьшим SSE. <br />
-
Четко видно, что лучший результат достигается при значении параметра = 0.5. В остальных случаях алгоритм попадает в локальный минимум, далекий от оптимального решения. <br />
+
[[Изображение:SSE( number of generations ) for varyingCrossoverFraction!.png|600px]] <br />
-
[[Изображение:Least squares linear fit, varyingCrossoverFraction(value1).png|1000px]] <br />
+
Разницы в эффективности для различных значений доли кроссинговера нет. Для всех 3 значений training-графики быстро сливаются (начиная с 30-ой итерации), test-графики достаточно близки.<br />
-
Ранняя сходимость: правый красный конец недостаточно загнул, левый синий - слишком. <br />
+
[[Изображение:Least squares linear fit, varyingCrossoverFraction(value1)!.png|300px]]
-
[[Изображение:Least squares linear fit, varyingCrossoverFraction(value2).png|1000px]] <br />
+
[[Изображение:Least squares linear fit, varyingCrossoverFraction(value2)!.png|300px]]
-
Лучший результат. <br />
+
[[Изображение:Least squares linear fit, varyingCrossoverFraction(value3)!.png|300px]] <br />
-
[[Изображение:Least squares linear fit, varyingCrossoverFraction(value3).png|1000px]] <br />
+
На всех 3 графиках видно, что поверхности почти не отличаются, все очень похожи на данные выборки.
-
Ранняя сходимость, ситуация аналогична 0.3.
+
-
=== Выводы ===
+
==== Выводы ====
-
Подтверждаются выводы, сделанные для модельных данных.
+
Подтверждаются выводы, сделанные для модельных данных с большой дисперсией.
== Исходный код ==
== Исходный код ==
-
Скачать код MATLAB можно здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/gaLinRegressionFeatureSelection/createArtificialData1D.m createArtificialData1D.m],
+
Скачать код MATLAB можно здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group774/Savinov2010Genetic/]. <br />
-
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/gaLinRegressionFeatureSelection/testGaEffeciency.m testGaEffeciency.m],
+
Скачать реальные данные по опционам можно здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group774/Savinov2010Genetic/realOptions2D.txt realOptions2D.txt].
-
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/gaLinRegressionFeatureSelection/gaEffeciency.m gaEffeciency.m],
+
-
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/gaLinRegressionFeatureSelection/evalSSE.m evalSSE.m],
+
-
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/gaLinRegressionFeatureSelection/plotRes.m plotRes.m],
+
-
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/gaLinRegressionFeatureSelection/plotRegression.m plotRegression.m]. <br />
+
-
Скачать реальные данные по опционам можно здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/gaLinRegressionFeatureSelection/realOptions2D.txt realOptions2D.txt].
+
-
== Смотри также ==
+
== Смотрите также ==
* [[Генетический алгоритм]]
* [[Генетический алгоритм]]
 +
* [[Теорема схемы]]
* [[Регрессионный анализ]]
* [[Регрессионный анализ]]
* [[Линейная регрессия (пример)]]
* [[Линейная регрессия (пример)]]
 +
* [[Метод наименьших квадратов]]
== Литература ==
== Литература ==
-
* Matlab 7.9.0(R2009b), Product Help\Genetic algorith options.
+
* Zbigniew Michalevicz, "Genetic Algorithms + Data Structures = Evolution Programs" (chapter 3: "GAs: Why Do They Work?").
-
{{Задание|Николай Савинов|В.В. Стрижов|28 мая 2010}}
+
* Melanie Mitchell, "An Introduction to Genetic Algorithms".
-
[[Категория:Учебные материалы]]
+
{{ЗаданиеВыполнено|Nikolay Savinov|V.V. Strijov|20 июня 2010}}
 +
[[Категория:Практика и вычислительные эксперименты]]

Текущая версия

Содержание

Генетический алгоритм — эвристический алгоритм поиска, используется для решения задач оптимизации. Название обусловлено смыслом эвристики: моделируется биологический естественный отбор, степень приспособленности определяется значением целевой функции. Возможно применение генетического алгоритма для выбора признаков линейной регрессии, поскольку данная задача допускает оптимизационную формулировку (если множество порождающих функций зафиксировано).

Постановка задачи

Задана выборка — множество \{x_1,...,x_n|x_i\in\mathbb{R}^M\} значений свободных переменных и множество \{y_1,...,y_n| y_i\in\mathbb{R}\} соответствующих им значений зависимой переменной. Задано множество порождающих функций линейной регрессионной модели \{\mathbf{f}_1,...,\mathbf{f}_N\}, где \mathbf{f}_i:\: \mathbb{R}^M \to \mathbb{R}. Введем обозначения:
c\in\{0,1\}^N, F(c) =\left(\begin{array}{ccc} \mathbf{f}_{i_1}(x_1) & \ldots & \mathbf{f}_{i_k}(x_1)\\ \mathbf{f}_{i_1}(x_2) & \ldots & \mathbf{f}_{i_k}(x_2)\\ \ldots & \ldots & \ldots \\ \mathbf{f}_{i_1}(x_n) & \ldots & \mathbf{f}_{i_k}(x_n)\\ \end{array} \right), k = ||c||_1,\; {\{i_j\}_{j=1}}^k \subset \{ 1,...,N \}\;: \; c(i_j)=1 при j=1,...,k;
\mathbf{w(c)} = (F(c)^TF(c))^{-1}F(c)^T\mathbf{y};
\mathbf{y(c)} = F(c)\mathbf{w(c)}.
Требуется решить следующую задачу:
SSE(c) = (\mathbf{y}-\mathbf{y(c)})^T(\mathbf{y}-\mathbf{y(c)}) \to min_c.

Описание алгоритма

Свободные параметры: размер популяции, доля кроссинговера (доля особей одного поколения, подвергающихся кроссинговеру).

  1. Инициализация (создание начальной популяции необходимого размера). Хромосомы особей представляют собой битовые векторы со случайными компонентами. Счетчик числа итераций: n:=0.
  2. n:=n+1. Проверка условий завершения: либо n превысило максимально допустимое значение, либо изменения целевой функции SSE для лучшей особи в популяции за некоторое число итераций оказалось слишком малым.
  3. Селекция (выбор особей для следующего поколения). Селекция выполняется на основе оценки SSE всех особей. Используемый механизм таков: на единичном отрезке каждой особи выделяется участок, длина которого пропорциональна SSE. Далее алгоритм-селектор движется вдоль отрезка с фиксированным шагом, выбирая каждый раз ту особь, над которой находится. Начальная точка выбирается случайно, при этом начальное расстояние до левого конца должно быть меньше шага.
  4. Кроссинговер. Выбирается число особей, равное доли кроссинговера * размер популяции. С парами особей выполняется так называемый кроссинговер с маской (см. Оператор скрещивания). В результате этой операции каждая аллель (т. е. позиция в хромосоме особи) случайным образом заполняется геном 1-ого или 2-ого родителя.
  5. Мутация. Для каждой особи в каждой аллели с вероятностью 0.01 происходит мутация, которая выражается в замене текущего гена на 0 или 1 случайным образом (равновероятно).
  6. Возвращение на шаг 2.

Замечание

Существует еще одна модификация оператора кроссинговера - одноточечная, когда случайным образом выбирается позиция в хромосоме, и хромосомы особей обмениваются подстроками, заключенными между этой позицией и правым концом строки (см. Оператор скрещивания). Для этой модификации справедлива теорема схемы, которая имеет наглядную интерпретацию в терминах рассматриваемой задачи. Кратко изложим основную идею.
Пусть имеется какая-то начальная популяция. Рассмотрим некоторую совокупность признаков, не очень большую и имеющую не очень большое расстояние между крайними левыми и правыми позициями в хромосоме, дающую приближение в смысле SSE лучше, чем в среднем по данной популяции. Тогда количество появлений такой совокупности признаков в последующих популяциях будет расти экспоненциально на протяжении некоторого числа популяций. Таким образом, наборы признаков с высоким качеством сохраняются и распространяются по популяции.
Однако в данном исследовании используется кроссинговер с маской, для которого теорема схемы формально не может применяться.

Вычислительный эксперимент

Показана работа алгоритма на реальных и модельных данных.

Модельные данные

Данные порождались следующим образом (D - дисперсия): 

x = [ 1:0.5:20 ]';
y = x + x.^2 + sin( x ) + log( x ) + x.*log( x ) + ( x.^2 ).*sin( x ) + sqrt( D ) * randn( size( x, 1 ), 1 );

Выборка делилась на training и testing части в соотношении 60%:40% случайным образом. Исследовались 2 эффекта: ложная (ранняя) сходимость и переобучение.

Результаты на модельных данных

Использовался следующий набор порождающих функций (всего 12):
1,\; x,\; x^2,\; log(x),\; x^3,\; x*log(x),\; x^4,\; x^2*log(x),\; x^2*cos(x),\; cos(x)*log(x),\; x*sin(x)*log(x),\; x^2*cos(x)*log(x).
В наборе не было следующих функций, участвовавших в порождении: sin(x),\; x^2*sin(x).

Случай небольшой дисперсии (D=1)


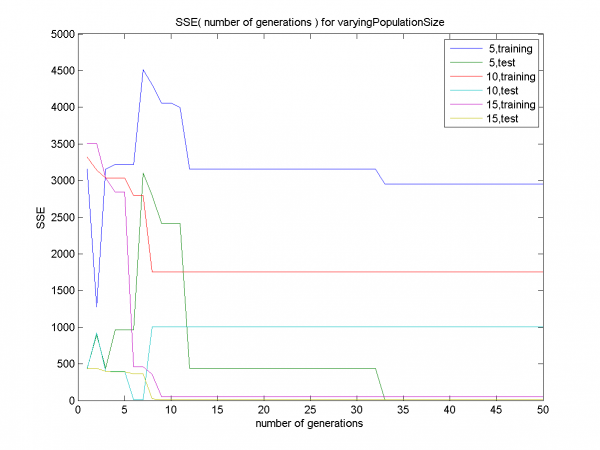
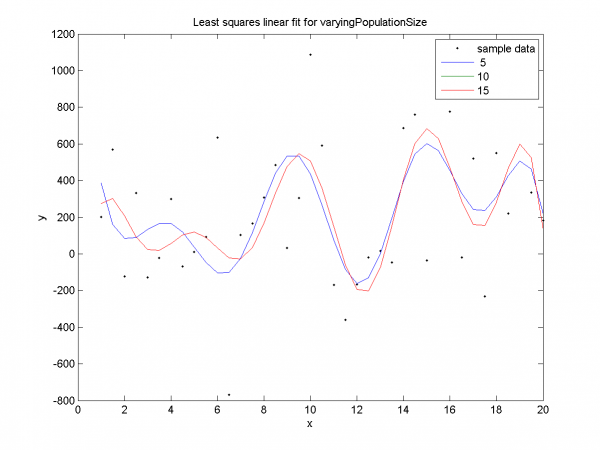
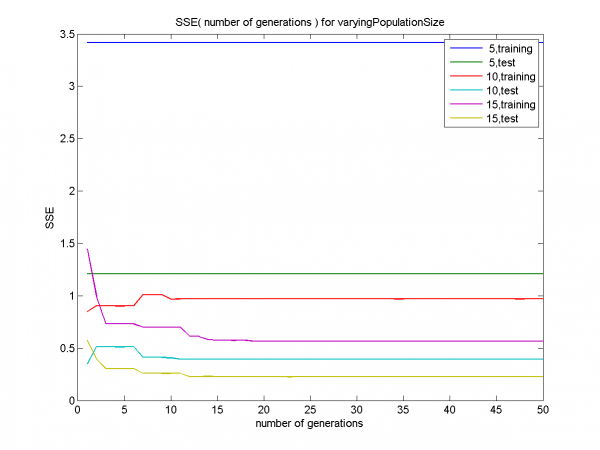
График для размера популяции 5 демонстрирует раннюю сходимость на обучающем множестве (training,5). Графики для размера популяции 10 демонстрируют раннюю сходимость и переобучение (т.е. SSE мало на обучающем множестве и велико на контрольном). Графики для размера популяции 15 показывают сходимость без переобучения.

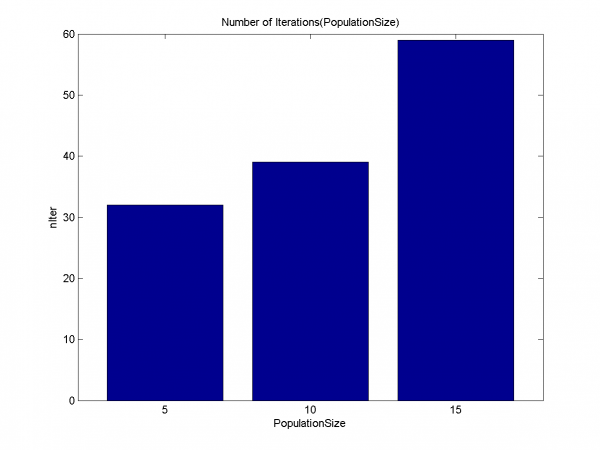
Подтверждение ранней сходимости для размеров популяции 5, 10. Дольше всего алгоритм работает для значения 15.

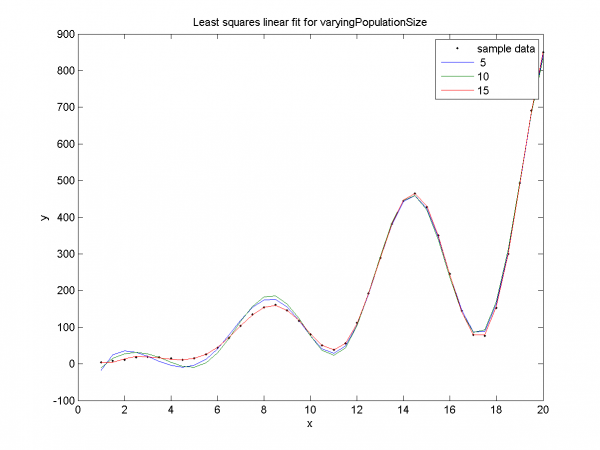
Наглядная демонстрация ранней сходимости и переобучения. Для размеров популяции 5, 10 SSE мало на training-части и велико на test-части. Для размера популяции 15 - подтверждается отсутствие ранней сходимости, переобучения.

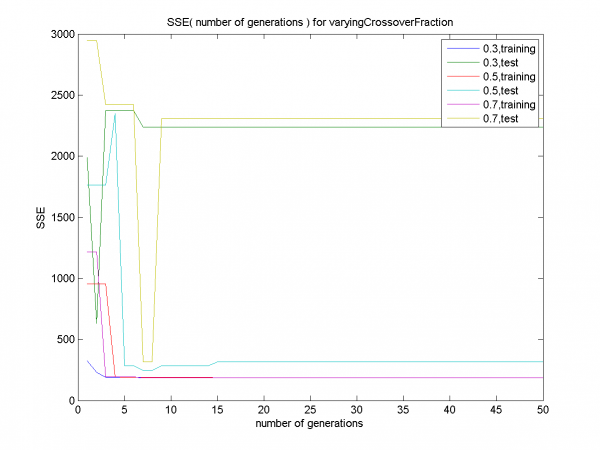
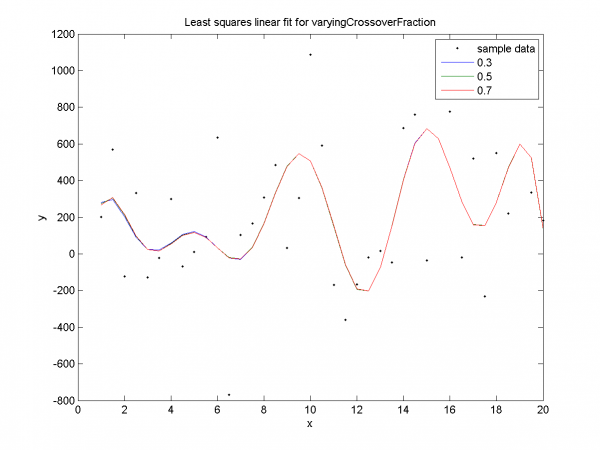
Графики для долей кроссинговера 0.3, 0.7 характеризуются переобучением. Для доли кроссинговера 0.5 переобучение не наблюдается, только ранняя сходимость.


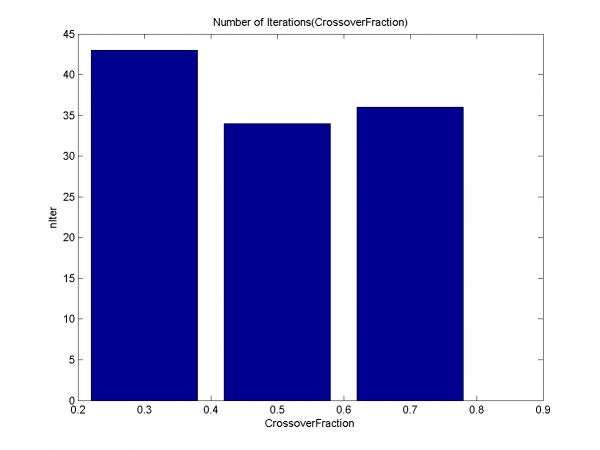
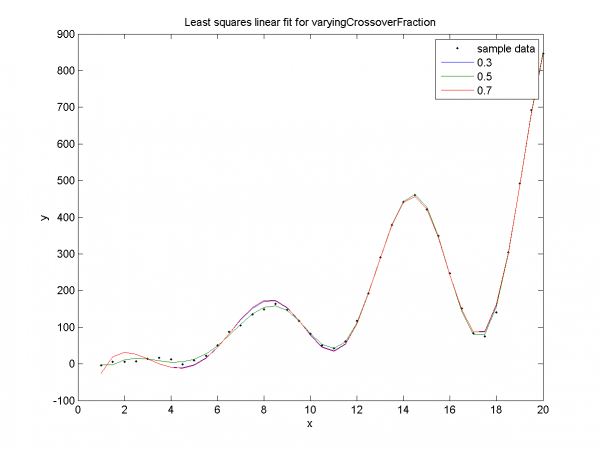
Наглядная демонстрация переобучения для долей кроссинговера 0.3, 0.7. Для значения 0.5 нет явного переобучения, как уже было замечено ранее.

Выводы

Чем больше размер популяции, тем менее вероятно переобучение и ранняя сходимость. Оптимальное значение доли кроссинговера равно 0.5.

Случай значительной дисперсии (D=160000)


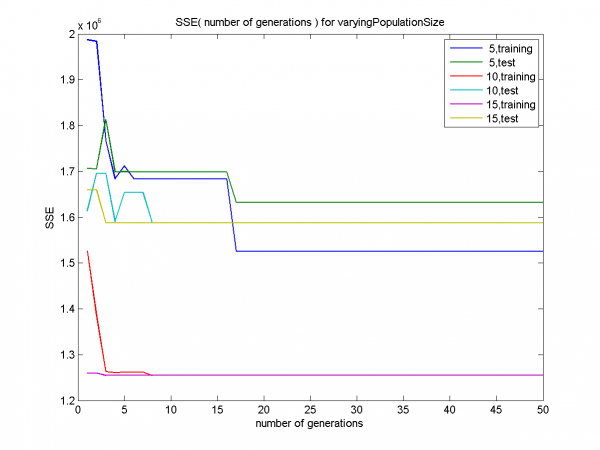
Видно, что для размера популяции 5 результатом работы алгоритма является точка пространства поиска с SSE значительно большим, чем для размеров популяции 10, 15.

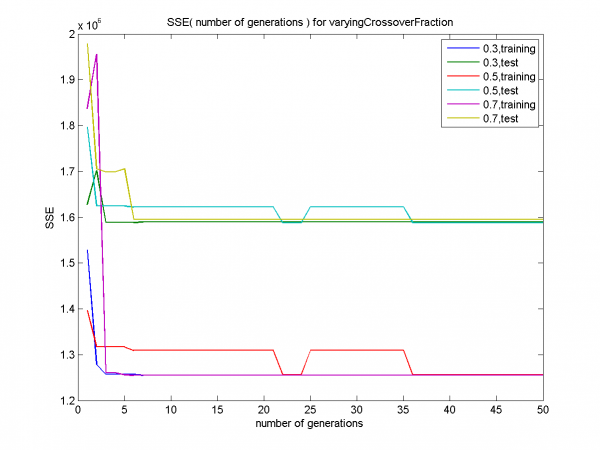
Начиная с 36-ой итерации все графики сливаются.

Четко видно отклонение синей линии, соответствующей размеру популяции 5, от линий, соответствующих значениям 10, 15 (эти линии сливаются). Графики SSE для всех значений, приведенные ранее, показали, что SSE для итоговой точки при значении 5 больше SSE в случаях 10, 15.

Все 3 графика сливаются, как уже было замечено ранее.

Выводы

При значительном шуме зависимость эффективности от доли кроссинговера очень слабая. Однако зависимость от размера популяции по-прежнему заметна, чем больше значение этого параметра - тем лучше.

Реальные данные

Выборка с улыбкой волатильности. 2 независимые переменные: время и страйк, зависимая переменная - волатильность. Выборка делилась как и прежде.

Результаты на реальных данных

Использовался следующий набор порождающих функций (всего 26):
1,\; x(1),\; x(1)^2,\; x(1)^3,\; x(1)^4,\; x(2),\; x(2)^2,\; x(2)^3,\; x(2)^4,\; sin(x(1)),\; sin(x(2)),\; x(1)*x(2),\; x(1)*x(2)^2,\; x(1)*x(2)^3,\; x(1)*x(2)^4,
x(1)^2*x(2),\; x(1)^2*x(2)^2,\; sin(x(1))*x(2),\; sin(x(1))*x(2)^2,\; sin(x(2))*x(1),\; sin(x(2))*x(1)^2,\; 1/(x(1)+0.1),\; 1/(x(2)+0.1),
log(0.1+x(1)),\; log(0.1+x(2)),\; exp(x(1)).


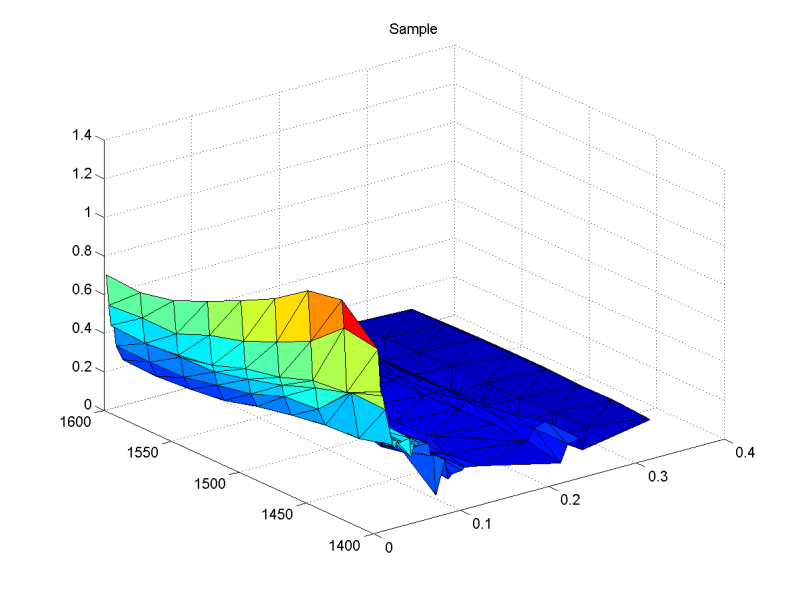
Результат с наименьшим SSE - при размере популяции 15, с наибольшим SSE - при размере популяции 5.

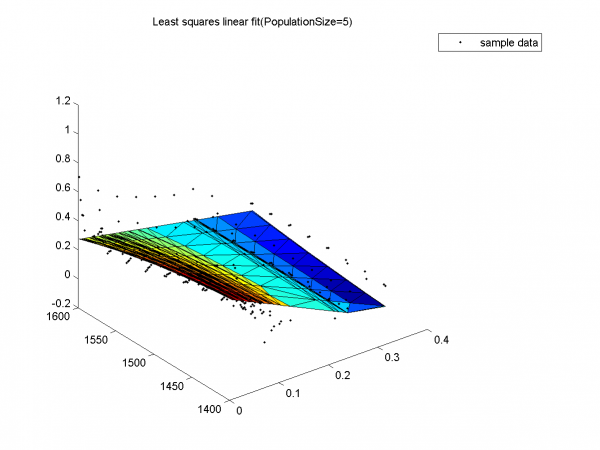
Результат с наибольшим SSE. Никакого сходства с данными.

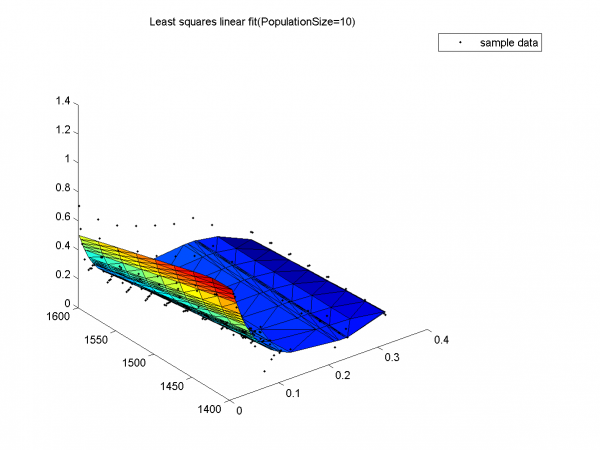
Неплохой результат, но видно, что красный край недостаточно загнут вверх относительно исходных данных, что выражается в большом значении SSE по сравнению с результатом для размера популяции 15.

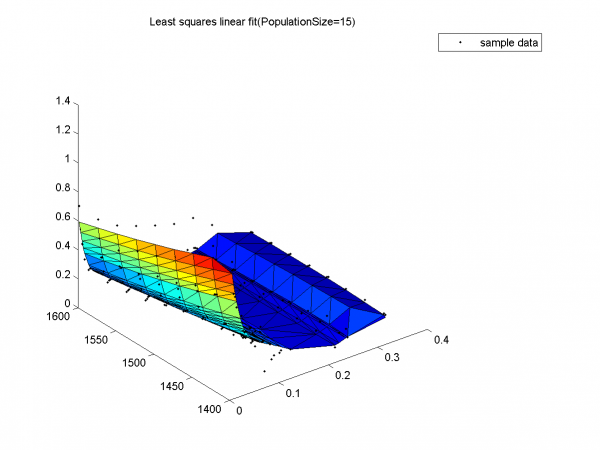
Результат с наименьшим SSE.

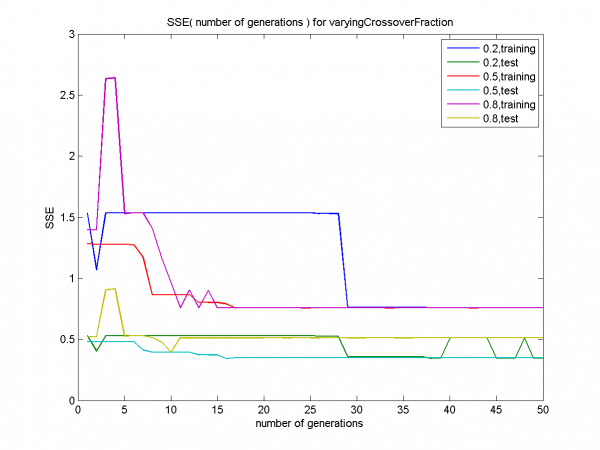
Разницы в эффективности для различных значений доли кроссинговера нет. Для всех 3 значений training-графики быстро сливаются (начиная с 30-ой итерации), test-графики достаточно близки.

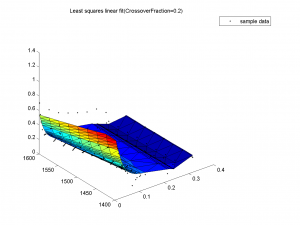
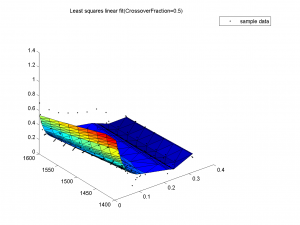
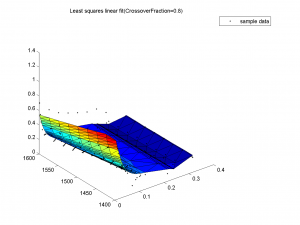
На всех 3 графиках видно, что поверхности почти не отличаются, все очень похожи на данные выборки.

Выводы

Подтверждаются выводы, сделанные для модельных данных с большой дисперсией.

Исходный код

Скачать код MATLAB можно здесь: [1].
Скачать реальные данные по опционам можно здесь: realOptions2D.txt.

Смотрите также

Литература

  • Zbigniew Michalevicz, "Genetic Algorithms + Data Structures = Evolution Programs" (chapter 3: "GAs: Why Do They Work?").
  • Melanie Mitchell, "An Introduction to Genetic Algorithms".
Данная статья была создана в рамках учебного задания.
Студент: Участник:Nikolay Savinov
Преподаватель: Участник:V.V. Strijov
Срок: 20 июня 2010


В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%92%D1%8B%D0%B1%D0%BE%D1%80_%D0%BF%D1%80%D0%B8%D0%B7%D0%BD%D0%B0%D0%BA%D0%BE%D0%B2_%D1%81_%D0%BF%D0%BE%D0%BC%D0%BE%D1%89%D1%8C%D1%8E_%D0%B3%D0%B5%D0%BD%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC%D0%BE%D0%B2_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты