Прогнозирование временных рядов методом SSA (пример)
Материал из MachineLearning.
| (31 промежуточная версия не показана) | |||
| Строка 1: | Строка 1: | ||
'''SSA (Singular Spectrum Analysis, "Гусеница")''' - метод анализа и прогноза временных рядов. | '''SSA (Singular Spectrum Analysis, "Гусеница")''' - метод анализа и прогноза временных рядов. | ||
| - | Базовый вариант метода состоит в: | + | Базовый вариант метода состоит в: |
| + | |||
| + | 1) преобразовании одномерного ряда в многомерный с помощью однопараметрической сдвиговой процедуры (отсюда и название "Гусеница"); | ||
| + | |||
| + | 2) исследовании полученной многомерной траектории с помощью анализа главных компонент (сингулярного разложения); | ||
| + | |||
| + | 3) восстановлении (аппроксимации) ряда по выбранным главным компонентам. | ||
| + | |||
Таким образом, результатом применения метода является разложение временного ряда на простые компоненты: медленные тренды, сезонные и другие периодические или колебательные составляющие, а также шумовые компоненты. | Таким образом, результатом применения метода является разложение временного ряда на простые компоненты: медленные тренды, сезонные и другие периодические или колебательные составляющие, а также шумовые компоненты. | ||
Полученное разложение может служить основой прогнозирования как самого ряда, так и его отдельных составляющих. "Гусеница" допускает естественное обобщение на многомерные временные ряды, а также на случай анализа изображений. | Полученное разложение может служить основой прогнозирования как самого ряда, так и его отдельных составляющих. "Гусеница" допускает естественное обобщение на многомерные временные ряды, а также на случай анализа изображений. | ||
| - | В данной статье рассмотрим вариант алгоритма, предназначенный для анализа многомерного временного ряда. | + | В данной статье рассмотрим вариант алгоритма, предназначенный для анализа многомерного временного ряда. |
| - | + | Алгоритм содержит два входных параметра [[Многомерная гусеница, выбор длины и числа компонент гусеницы (пример)|длину гусеницы и число ее компонент]], выбор которых существенно влияет на результат работы алгоритма. | |
== Постановка задачи == | == Постановка задачи == | ||
| - | Наблюдается система функций дискретного аргумента {<tex>$(f_i^{(k)})_{i=1}^N$</tex>, где k = 1, ..., s}. | + | Наблюдается система функций дискретного аргумента {<tex>$(f_i^{(k)})_{i=1}^N$</tex>, где k = 1, ..., s}. s - число временных рядов, k - номер ряда, N - длина временного ряда, i - номер отсчета. Требуется разложить ряд в сумму компонент (используя метод главных компонент, см. описание алгоритма), интерпретировать каждую компоненту, и построить продолжение ряда <tex>$(f_i^{(k)})_{i=1}^{N+M}$</tex> по выбранным компонентам. |
| - | + | ||
== Описание алгоритма == | == Описание алгоритма == | ||
| - | Выберем n такое, что <tex>$0 < n \le N - 1$</tex> - время жизни многомерной гусеницы. Пусть <tex>$\sigma = N - n + 1$</tex> - длина гусеницы. Построим последовательность из n векторов в <tex>$R^{\ | + | === Построение матрицы наблюдений === |
| + | Рассмотрим сначала одномерный временной ряд <tex>$(f_i)_{i=1}^N.$</tex> Выберем n такое, что <tex>$0 < n \le N - 1$</tex> - время жизни многомерной гусеницы. Пусть <tex>$\sigma = N - n + 1$</tex> - длина гусеницы. Построим последовательность из n векторов в <tex>$R^{\sigma}$</tex> следующего вида: | ||
| + | |||
| + | <tex>Y^{(l)} \in R^{\sigma},</tex> <tex>Y^{(l)} = (f_{i+l-1})_{i=1}^{\sigma}</tex> | ||
| - | + | Обозначим | |
| - | + | <tex>$$Z = (Y^{(1)}, \ldots, Y^{(n)}):$$</tex> | |
| - | + | [[Изображение:newpic7.png|800px]] | |
| - | |||
| - | Рассмотрим ковариационную матрицу полученной | + | Будем называть <tex>$Z$</tex> нецентрированной матрицей наблюдений, порождённой гусеницей со временем жизни n. |
| + | |||
| + | В случае многомерного временного ряда матрицей наблюдения называется столбец из матриц наблюдений, соответствующих каждой из компонент. | ||
| + | |||
| + | Проводимый в дальнейшем анализ главных компонент может проводиться как по центрированной, так и по нецентрированной выборкам. Для упрощения выкладок рассмотрим простейший нецентрированный вариант. | ||
| + | |||
| + | === Анализ главных компонент === | ||
| + | Рассмотрим ковариационную матрицу полученной выборки: | ||
<tex>$$C = \frac1n ZZ^T.$$</tex> | <tex>$$C = \frac1n ZZ^T.$$</tex> | ||
| Строка 35: | Строка 50: | ||
<tex>$$U = V^T Z, U = (U^{(1)}, \ldots, U^{(\tau)})^T.$$</tex> | <tex>$$U = V^T Z, U = (U^{(1)}, \ldots, U^{(\tau)})^T.$$</tex> | ||
| - | После проведения анализа главных компонент обычно предполагается проведение операции восстановления исходной матрицы наблюдений по некоторому поднабору главных компонент, т. е. для <tex>$V' = (v^{(i_1)}, \ldots, v^{(i_r)})$</tex> и <tex>$U' = V'^T Z$</tex> вычисляется матрица <tex>$Z' = V'U'$</tex>. Далее восстанавливаются исходные последовательности: | + | После проведения анализа главных компонент обычно предполагается проведение операции восстановления исходной матрицы наблюдений по некоторому поднабору главных компонент, т. е. для <tex>$V' = (v^{(i_1)}, \ldots, v^{(i_r)})$</tex> и <tex>$U' = V'^T Z$</tex> вычисляется матрица <tex>$Z' = V'U'$</tex>. |
| + | |||
| + | Далее восстанавливаются исходные последовательности. В одномерном случае i-ая компонента восстановленного ряда есть среднее значение по i-ой диагонали восстановленной матрицы наблюдений <tex>Z'</tex>: | ||
| + | |||
| + | [[Изображение:newpic6.png|425px]] | ||
| + | |||
| + | В многомерном случае усреднение проводится с учётом того, что матрица наблюдений состоит из подматриц, соответствующих каждой компоненте ряда: | ||
<tex>$$f'_m^{(k)} = \left\{ \begin{array}{ll} \frac1m \sum_{i=1}^m x_i^{(m-i+1,k)}&1\le m\le \sigma,\\ \frac{1}{\sigma} \sum_{i=1}^{\sigma} x_i^{(m-i+1,k)}&\sigma \le m \le n,\\ \frac{1}{N-m+1} \sum_{i=1}^{N-m+1} x_{i+m-n}^{(n-i+1,k)}&n \le m \le N.\end{array} \right$$</tex> | <tex>$$f'_m^{(k)} = \left\{ \begin{array}{ll} \frac1m \sum_{i=1}^m x_i^{(m-i+1,k)}&1\le m\le \sigma,\\ \frac{1}{\sigma} \sum_{i=1}^{\sigma} x_i^{(m-i+1,k)}&\sigma \le m \le n,\\ \frac{1}{N-m+1} \sum_{i=1}^{N-m+1} x_{i+m-n}^{(n-i+1,k)}&n \le m \le N.\end{array} \right$$</tex> | ||
| - | Определим | + | === Прогноз === |
| + | Числовой ряд <tex>(f_i)_{i=1}^{N+1}</tex> называется продолжением ряда <tex>(f_i)_{i=1}^N</tex>, если порождаемая им при гусеничной обработке выборка лежит в той же гиперплоскости, что и у исходного ряда. Пусть у нас есть некоторый набор выбранных главных компонент <tex>i_1, i_2, \ldots, i_r.</tex> Определим | ||
<tex>$$w = \left ( \begin{array}{cccc} v_{\sigma}^{(i_1)}&v_{\sigma}^{(i_2)}&\ldots&v_{\sigma}^{(i_r)}\\ v_{2\sigma}^{(i_1)}&v_{2\sigma}^{(i_2)}&\ldots&v_{2\sigma}^{(i_r)}\\ \vdots& \vdots &\ddots & \vdots\\ v_{\tau}^{(i_1)}&v_{\tau}^{(i_2)}&\ldots&v_{\tau}^{(i_r)}\end{array} \right ) $$</tex> | <tex>$$w = \left ( \begin{array}{cccc} v_{\sigma}^{(i_1)}&v_{\sigma}^{(i_2)}&\ldots&v_{\sigma}^{(i_r)}\\ v_{2\sigma}^{(i_1)}&v_{2\sigma}^{(i_2)}&\ldots&v_{2\sigma}^{(i_r)}\\ \vdots& \vdots &\ddots & \vdots\\ v_{\tau}^{(i_1)}&v_{\tau}^{(i_2)}&\ldots&v_{\tau}^{(i_r)}\end{array} \right ) $$</tex> | ||
| Строка 51: | Строка 73: | ||
<tex>$$Q = \left (f_{N-\sigma+2}^{(1)}, \ldots, f_N^{(1)}, f_{N-\sigma+2}^{(2)}, \ldots, f_N^{(2)}, \ldots, f_{N-\sigma+2}^{(s)}, \ldots, f_N^{(s)}\right )^T$$</tex> | <tex>$$Q = \left (f_{N-\sigma+2}^{(1)}, \ldots, f_N^{(1)}, f_{N-\sigma+2}^{(2)}, \ldots, f_N^{(2)}, \ldots, f_{N-\sigma+2}^{(s)}, \ldots, f_N^{(s)}\right )^T$$</tex> | ||
| - | + | Тогда прогнозируемые значения системы в точке <tex>$N+1$</tex> вычисляются по формуле: | |
<tex>$$f_{N+1} = w(V_*^T V_*)^{-1} V_*^T Q.$$</tex> | <tex>$$f_{N+1} = w(V_*^T V_*)^{-1} V_*^T Q.$$</tex> | ||
| - | |||
== Численный эксперимент == | == Численный эксперимент == | ||
| Строка 62: | Строка 83: | ||
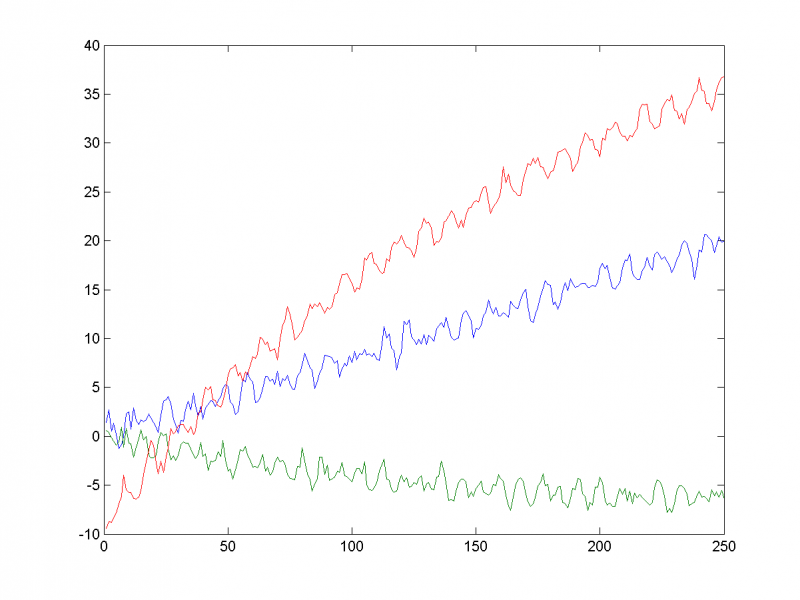
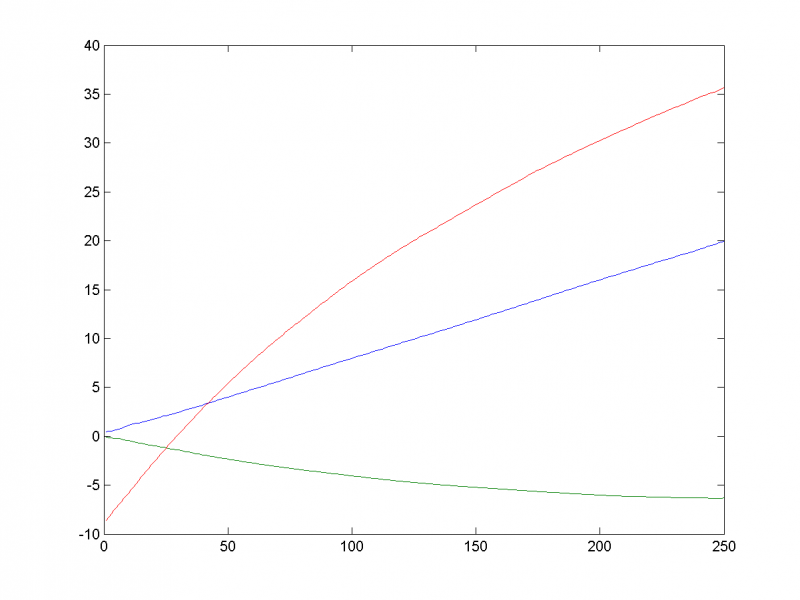
Рассмотрим трёхмерный временной ряд, заданный формулами: | Рассмотрим трёхмерный временной ряд, заданный формулами: | ||
| - | <tex>$$f_1(t) = 0,08t + 0,9\sin (\frac{2\pi t}{11}) + 0,8\sin (\frac{2\pi (t+0,09)}{8})$$</tex> | + | <tex>$$f_1(t) = 0,08t + 0,9\sin (\frac{2\pi t}{11}) + 0,8\sin \left(\frac{2\pi (t+0,09)}{8}\right),$$</tex> |
| - | <tex>$$f_2(t) = 0,0001t^2 - 0,05t + 0,6\sin (\frac{2\pi (t-0,14)}{11}) + \cos (\frac{2\pi t}{8})$$</tex> | + | <tex>$$f_2(t) = 0,0001t^2 - 0,05t + 0,6\sin (\frac{2\pi (t-0,14)}{11}) + \cos \left(\frac{2\pi t}{8}\right),$$</tex> |
| - | <tex>$$f_3(t) = 36\log(t+100) - 1,2\sin (\frac{2\pi (t+0,24)}{11}) + 0,5\sin (\frac{2\pi (t-0,35)}{8})$$</tex> | + | <tex>$$f_3(t) = 36\log(t+100) - 1,2\sin (\frac{2\pi (t+0,24)}{11}) + 0,5\sin \left(\frac{2\pi (t-0,35)}{8}\right),$$</tex> |
| - | <tex>$$t = 1, 2, \ldots, 250$$</tex> | + | где <tex>$$t = 1, 2, \ldots, 250$$</tex> |
Кроме тренда (линейная, квадратичная функции и логарифм соответственно) в ряды добавлены две периодические составляющие (синусоиды с различными амплитудами и фазами). Также во временные ряды добавлен шум со среднеквадратичным отклонением 0,5: | Кроме тренда (линейная, квадратичная функции и логарифм соответственно) в ряды добавлены две периодические составляющие (синусоиды с различными амплитудами и фазами). Также во временные ряды добавлен шум со среднеквадратичным отклонением 0,5: | ||
| - | [[Изображение: | + | [[Изображение:newpic1.png|800px]] |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
Исследуем главные компоненты данного временного ряда, используя гусеницу длины 50. | Исследуем главные компоненты данного временного ряда, используя гусеницу длины 50. | ||
| Строка 82: | Строка 99: | ||
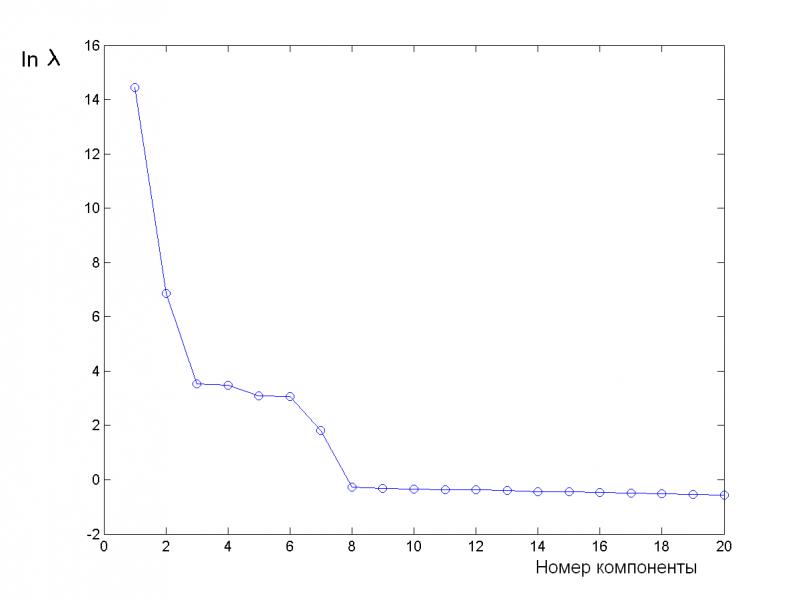
Логарифмы первых двадцати собственных чисел ковариационной матрицы: | Логарифмы первых двадцати собственных чисел ковариационной матрицы: | ||
| - | [[Изображение: | + | [[Изображение:newpic2.png|800px]] |
Из графика видно, что содержательный смысл несут, вероятно, первые семь главных компонент, а остальные, скорее всего, шум. | Из графика видно, что содержательный смысл несут, вероятно, первые семь главных компонент, а остальные, скорее всего, шум. | ||
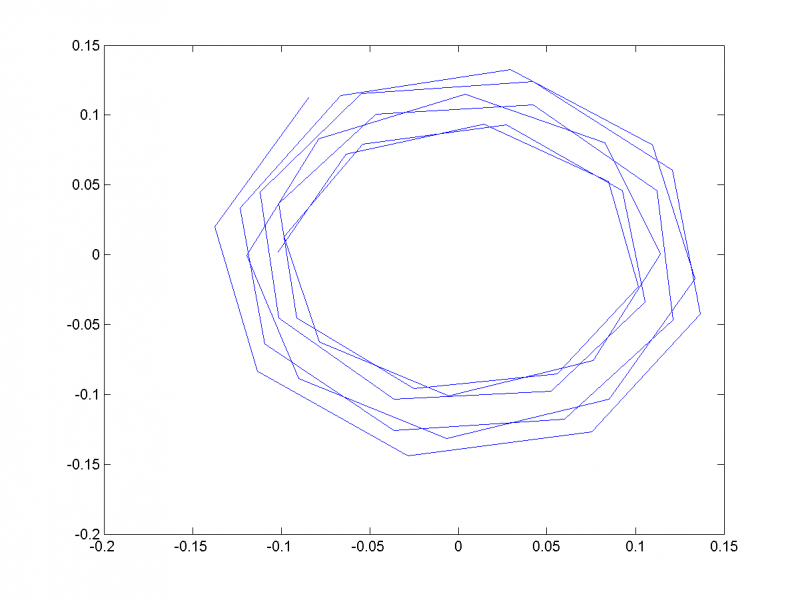
| - | + | Паре близких собственных чисел соответствуют главные компоненты, отвечающие одной частоте. Отложим на одном графике главные векторы, отвечающие 3-му и 4-му собственным числам. Покажем, что они кореллируют и соответствуют периодической составляющей с периодом 11: | |
[[Изображение:model6.png|800px]] | [[Изображение:model6.png|800px]] | ||
| Строка 94: | Строка 111: | ||
[[Изображение:model110.png|800px]] | [[Изображение:model110.png|800px]] | ||
| - | 5-му и 6-му собственным числам соответствует периодическая составляющая с периодом 8 | + | Аналогично, 5-му и 6-му собственным числам соответствует периодическая составляющая с периодом 8. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
1-я, 2-я и 7-я главная компоненты отвечают за тренд: | 1-я, 2-я и 7-я главная компоненты отвечают за тренд: | ||
| - | [[Изображение: | + | [[Изображение:newpic3.png|800px]] |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Восстановим ряд по остальным главным компонентам, предполагая их шумовыми: | |
[[Изображение:model13.png|800px]] | [[Изображение:model13.png|800px]] | ||
| Строка 114: | Строка 123: | ||
Спрогнозируем временной ряд на 50 единиц вперёд по первым семи главным компонентам: | Спрогнозируем временной ряд на 50 единиц вперёд по первым семи главным компонентам: | ||
| - | [[Изображение: | + | [[Изображение:newpic4.png|800px]] |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
Видим, что прогноз вполне адекватен. | Видим, что прогноз вполне адекватен. | ||
| + | === Нарушения периодичности ряда === | ||
Посмотрим, как отреагирует алгоритм на нарушение периодичности временного ряда. Во второй половине временного ряда изменим частоту, амплитуду и фазу одной из периодик: | Посмотрим, как отреагирует алгоритм на нарушение периодичности временного ряда. Во второй половине временного ряда изменим частоту, амплитуду и фазу одной из периодик: | ||
| - | <tex>$$f_1(t) = 0,08t + 0,6\sin (\frac{2\pi t}{14}) + 0,8\sin (\frac{2\pi (t+0,09)}{8}) | + | <tex>$$f_1(t) = 0,08t + 0,6\sin (\frac{2\pi t}{14}) + 0,8\sin \left(\frac{2\pi (t+0,09)}{8}\right),$$</tex> |
| - | + | ||
| - | + | ||
| - | <tex>$$ | + | <tex>$$f_2(t) = 0,0001t^2 - 0,05t + 0,45\sin (\frac{2\pi (t-0,14)}{14}) + \cos \left(\frac{2\pi t}{8}\right),$$</tex> |
| - | <tex>$$t = | + | <tex>$$f_3(t) = 36\log(t+100) - 0,8\sin (\frac{2\pi (t+0,24)}{14}) + 0,5\sin \left(\frac{2\pi (t-0,35)}{8}\right),$$</tex> |
| - | + | где <tex>$$t = 1, 2, \ldots, 250$$</tex> | |
| - | + | В этом случае 2-я и 3-я главная компонента будет соответствовать той периодике, которую мы не изменили. | |
| - | 5-я и 6-я | + | 5-я и 6-я соответствует первой половине изменённой компоненты: |
[[Изображение:model22.png|800px]] | [[Изображение:model22.png|800px]] | ||
| Строка 145: | Строка 149: | ||
1-я, 2-я и 9-я отвечают тренду: | 1-я, 2-я и 9-я отвечают тренду: | ||
| - | |||
| - | |||
Таким образом, алгоритм устойчив к нарушениям периодичности - разным участкам временного ряда соответствуют различные главные компоненты. | Таким образом, алгоритм устойчив к нарушениям периодичности - разным участкам временного ряда соответствуют различные главные компоненты. | ||
| + | === Выбросы === | ||
Посмотрим поведение алгоритма в случае наличия выбросов. Мы добавили выброс в среднем в каждую 50-ю точку временного ряда. Первое собственное число в этом случае на несколько порядков больше остальных, график логарифмов собственных чисел со 2-го по 20-е представлен ниже: | Посмотрим поведение алгоритма в случае наличия выбросов. Мы добавили выброс в среднем в каждую 50-ю точку временного ряда. Первое собственное число в этом случае на несколько порядков больше остальных, график логарифмов собственных чисел со 2-го по 20-е представлен ниже: | ||
| Строка 162: | Строка 165: | ||
Рассмотрим ежемесячные данные о покрытии полушарий Солнца пятнами с 1876 года. | Рассмотрим ежемесячные данные о покрытии полушарий Солнца пятнами с 1876 года. | ||
| - | + | Для северного полушария: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Изображение:real2.png|800px]] | [[Изображение:real2.png|800px]] | ||
| Строка 173: | Строка 172: | ||
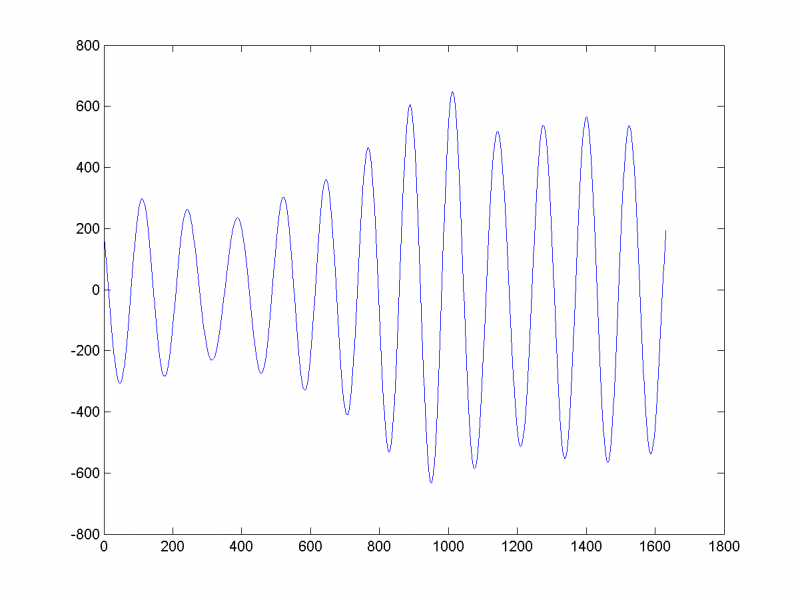
2-я и 3-я компоненты соответствуют 12-летним солнечным циклам: | 2-я и 3-я компоненты соответствуют 12-летним солнечным циклам: | ||
| - | |||
| - | |||
[[Изображение:real4.png|800px]] | [[Изображение:real4.png|800px]] | ||
| - | Автор статьи не смог интерпретировать остальные главные компоненты. Однако субъективно первые шесть главных вполне адекватно характеризуют солнечную активность и могут быть использованы для прогноза | + | Автор статьи не смог интерпретировать остальные главные компоненты. Однако субъективно первые шесть главных вполне адекватно характеризуют солнечную активность и могут быть использованы для прогноза. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== См. также == | == См. также == | ||
| - | * | + | * [[Временной ряд]] |
| - | * | + | * [[Метод главных компонент]] |
| - | + | * [http://www.gistatgroup.com/gus/index.html Сайт, посвящённый методу Гусеницы] | |
| + | * [http://strijov.com/sources/demo_ssa_forecast.php Простой пример прогноза] | ||
[[Категория:Прогнозирование временных рядов]] | [[Категория:Прогнозирование временных рядов]] | ||
== Литература == | == Литература == | ||
| - | * Главные компоненты временных рядов: | + | * А. А. Жиглявский, В. Н. Солнцев: "Главные компоненты временных рядов: метод "Гусеница" |
| - | + | * Vladimir Nekrutkin, Anatoly Zhigljavsky: "Analysis of Time Series Structure: SSA and Related Techniques". | |
| - | метод "Гусеница" | + | {{ЗаданиеВыполнено|Илья Фадеев|В.В.Стрижов|28 мая 2010}} |
| - | * Analysis of Time Series Structure: | + | |
| - | SSA and Related Techniques | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | {{ | + | |
[[Категория:Практика и вычислительные эксперименты]] | [[Категория:Практика и вычислительные эксперименты]] | ||
Текущая версия
SSA (Singular Spectrum Analysis, "Гусеница") - метод анализа и прогноза временных рядов. Базовый вариант метода состоит в:
1) преобразовании одномерного ряда в многомерный с помощью однопараметрической сдвиговой процедуры (отсюда и название "Гусеница");
2) исследовании полученной многомерной траектории с помощью анализа главных компонент (сингулярного разложения);
3) восстановлении (аппроксимации) ряда по выбранным главным компонентам.
Таким образом, результатом применения метода является разложение временного ряда на простые компоненты: медленные тренды, сезонные и другие периодические или колебательные составляющие, а также шумовые компоненты. Полученное разложение может служить основой прогнозирования как самого ряда, так и его отдельных составляющих. "Гусеница" допускает естественное обобщение на многомерные временные ряды, а также на случай анализа изображений. В данной статье рассмотрим вариант алгоритма, предназначенный для анализа многомерного временного ряда. Алгоритм содержит два входных параметра длину гусеницы и число ее компонент, выбор которых существенно влияет на результат работы алгоритма.
Содержание |
Постановка задачи
Наблюдается система функций дискретного аргумента {, где k = 1, ..., s}. s - число временных рядов, k - номер ряда, N - длина временного ряда, i - номер отсчета. Требуется разложить ряд в сумму компонент (используя метод главных компонент, см. описание алгоритма), интерпретировать каждую компоненту, и построить продолжение ряда
по выбранным компонентам.
Описание алгоритма
Построение матрицы наблюдений
Рассмотрим сначала одномерный временной ряд Выберем n такое, что
- время жизни многомерной гусеницы. Пусть
- длина гусеницы. Построим последовательность из n векторов в
следующего вида:
Обозначим
Будем называть нецентрированной матрицей наблюдений, порождённой гусеницей со временем жизни n.
В случае многомерного временного ряда матрицей наблюдения называется столбец из матриц наблюдений, соответствующих каждой из компонент.
Проводимый в дальнейшем анализ главных компонент может проводиться как по центрированной, так и по нецентрированной выборкам. Для упрощения выкладок рассмотрим простейший нецентрированный вариант.
Анализ главных компонент
Рассмотрим ковариационную матрицу полученной выборки:
Выполним её svd-разложение:
где - диагональная матрица собственных чисел,
,
- ортогональная матрица собственных векторов.
Далее рассмотрим систему главных компонент:
После проведения анализа главных компонент обычно предполагается проведение операции восстановления исходной матрицы наблюдений по некоторому поднабору главных компонент, т. е. для и
вычисляется матрица
.
Далее восстанавливаются исходные последовательности. В одномерном случае i-ая компонента восстановленного ряда есть среднее значение по i-ой диагонали восстановленной матрицы наблюдений :
В многомерном случае усреднение проводится с учётом того, что матрица наблюдений состоит из подматриц, соответствующих каждой компоненте ряда:
Прогноз
Числовой ряд называется продолжением ряда
, если порождаемая им при гусеничной обработке выборка лежит в той же гиперплоскости, что и у исходного ряда. Пусть у нас есть некоторый набор выбранных главных компонент
Определим
и
Также положим
Тогда прогнозируемые значения системы в точке вычисляются по формуле:
Численный эксперимент
Модельные данные
Рассмотрим трёхмерный временной ряд, заданный формулами:
где
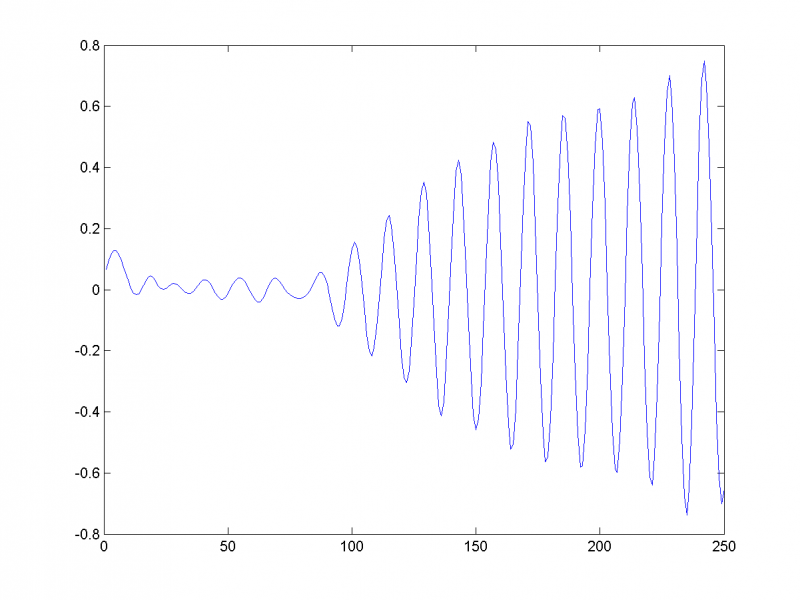
Кроме тренда (линейная, квадратичная функции и логарифм соответственно) в ряды добавлены две периодические составляющие (синусоиды с различными амплитудами и фазами). Также во временные ряды добавлен шум со среднеквадратичным отклонением 0,5:
Исследуем главные компоненты данного временного ряда, используя гусеницу длины 50.
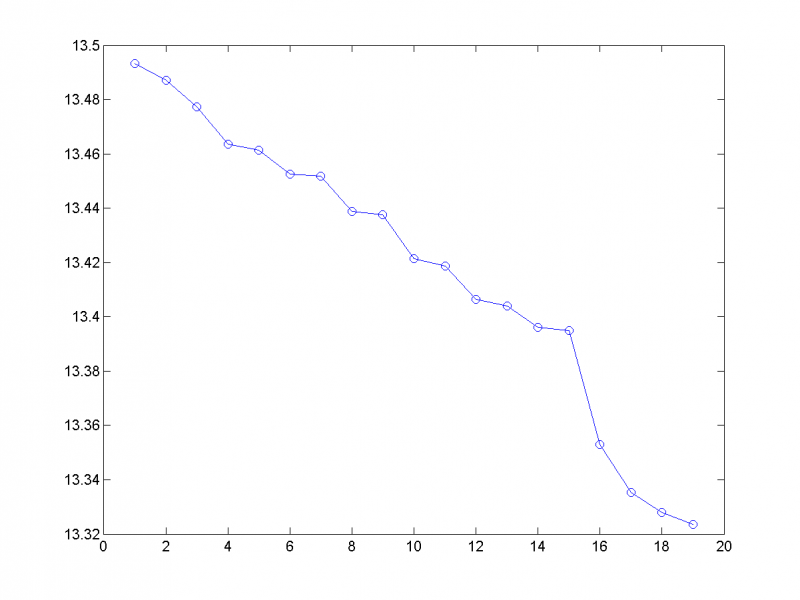
Логарифмы первых двадцати собственных чисел ковариационной матрицы:
Из графика видно, что содержательный смысл несут, вероятно, первые семь главных компонент, а остальные, скорее всего, шум.
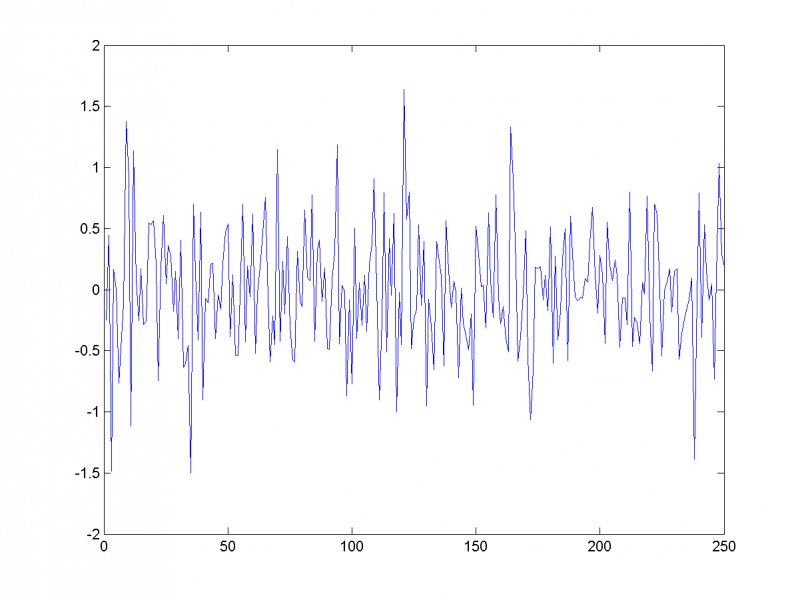
Паре близких собственных чисел соответствуют главные компоненты, отвечающие одной частоте. Отложим на одном графике главные векторы, отвечающие 3-му и 4-му собственным числам. Покажем, что они кореллируют и соответствуют периодической составляющей с периодом 11:
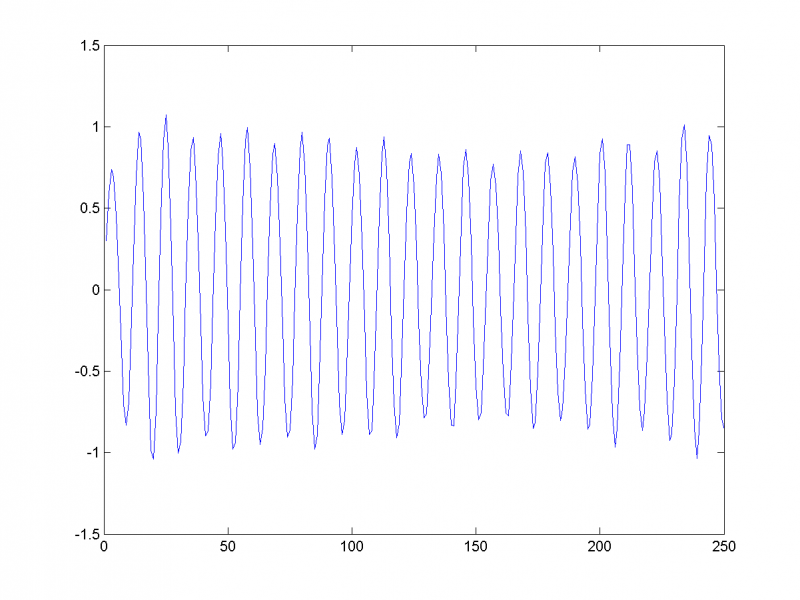
Восстановив временной ряд (на рисунке изображён первый из трёх) по этим двум главным компонентам, убеждаемся в этом:
Аналогично, 5-му и 6-му собственным числам соответствует периодическая составляющая с периодом 8.
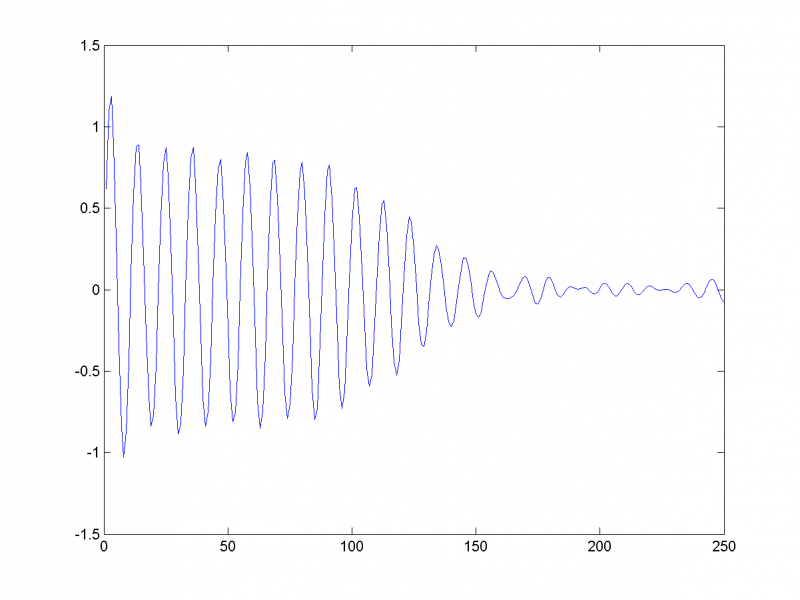
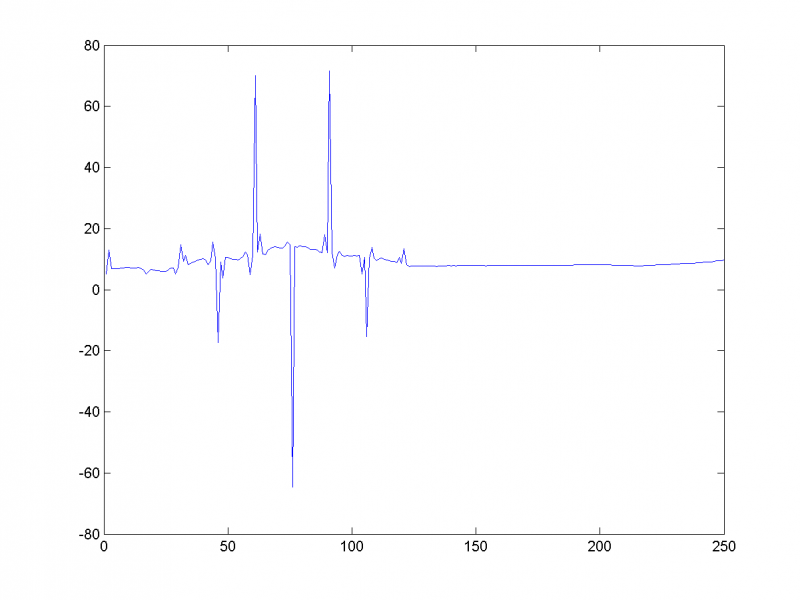
1-я, 2-я и 7-я главная компоненты отвечают за тренд:
Восстановим ряд по остальным главным компонентам, предполагая их шумовыми:
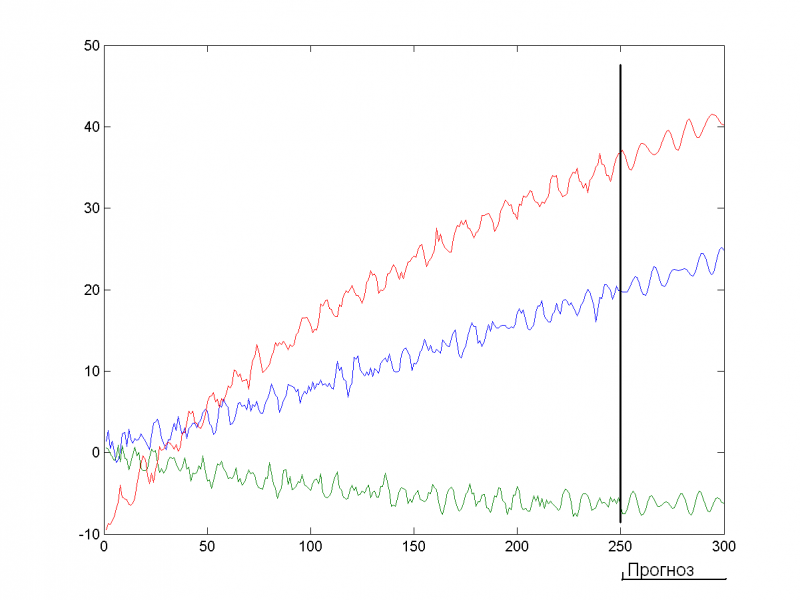
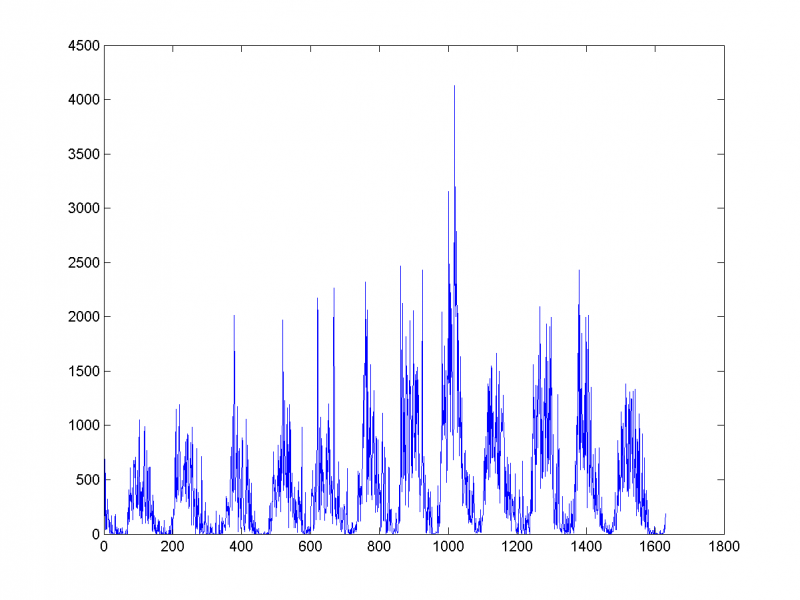
Спрогнозируем временной ряд на 50 единиц вперёд по первым семи главным компонентам:
Видим, что прогноз вполне адекватен.
Нарушения периодичности ряда
Посмотрим, как отреагирует алгоритм на нарушение периодичности временного ряда. Во второй половине временного ряда изменим частоту, амплитуду и фазу одной из периодик:
где
В этом случае 2-я и 3-я главная компонента будет соответствовать той периодике, которую мы не изменили.
5-я и 6-я соответствует первой половине изменённой компоненты:
7-я и 8-я - второй её половине:
1-я, 2-я и 9-я отвечают тренду:
Таким образом, алгоритм устойчив к нарушениям периодичности - разным участкам временного ряда соответствуют различные главные компоненты.
Выбросы
Посмотрим поведение алгоритма в случае наличия выбросов. Мы добавили выброс в среднем в каждую 50-ю точку временного ряда. Первое собственное число в этом случае на несколько порядков больше остальных, график логарифмов собственных чисел со 2-го по 20-е представлен ниже:
Восстанавливая ряд по первым 16-ти главным компонентам, видим, что алгоритм работает некорректно:
Реальные данные
Рассмотрим ежемесячные данные о покрытии полушарий Солнца пятнами с 1876 года.
Для северного полушария:
Используем гусеницу длины 250.
2-я и 3-я компоненты соответствуют 12-летним солнечным циклам:
Автор статьи не смог интерпретировать остальные главные компоненты. Однако субъективно первые шесть главных вполне адекватно характеризуют солнечную активность и могут быть использованы для прогноза.
См. также
Литература
- А. А. Жиглявский, В. Н. Солнцев: "Главные компоненты временных рядов: метод "Гусеница"
- Vladimir Nekrutkin, Anatoly Zhigljavsky: "Analysis of Time Series Structure: SSA and Related Techniques".
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |