Кластеризация графов без использования метрик (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Алгоритм)
(→Исходный код)
 
(9 промежуточных версий не показаны.)
Строка 12: Строка 12:
'''Определение.''' Вероятность, превышающую <tex>1-\frac1n</tex>, будем называть высокой.
'''Определение.''' Вероятность, превышающую <tex>1-\frac1n</tex>, будем называть высокой.
<br>
<br>
-
'''Определение.''' Вероятностный алгоритм, получающий на вход данные оптимизационной задачи и параметр <tex>\epsilon>0</tex>, который за полиномиальное время с высокой вероятностью получает решение, не более чем в <tex>(1+\epsilon)</tex> раз превышающее оптимальное, будем называть полиномиальной рандомизированной аппроксимационной схемой (PRAS).
+
'''Определение.''' Вероятностный алгоритм, получающий на вход данные оптимизационной задачи и параметр <tex>\varepsilon>0</tex>, который за полиномиальное время с высокой вероятностью получает решение, не более чем в <tex>(1+\varepsilon)</tex> раз превышающее оптимальное, будем называть полиномиальной рандомизированной аппроксимационной схемой (PRAS).
<br>
<br>
-
'''Определение.''' Если PRAS находит оптимальное решение с высокой вероятностью для любого <tex>\epsilon>0</tex>, то такой алгоритм будем называть вероятностным алгоритмом типа Монте-Карло.
+
'''Определение.''' Если PRAS находит оптимальное решение с высокой вероятностью для любого <tex>\varepsilon>0</tex>, то такой алгоритм будем называть вероятностным алгоритмом типа Монте-Карло.
В дальнейшем граф <tex>G</tex> будем считать связным, а веса ребер – единичными. Несколько слов о модификации алгоритма для решения задачи в случае взвешенного графа будет сказано в следующем разделе.
В дальнейшем граф <tex>G</tex> будем считать связным, а веса ребер – единичными. Несколько слов о модификации алгоритма для решения задачи в случае взвешенного графа будет сказано в следующем разделе.
Строка 25: Строка 25:
== Алгоритм ==
== Алгоритм ==
-
В качестве алгоритма для кластеризации предлагается использовать вероятностный алгоритм типа Монте-Карло, придуманный Каргером в работе [] для решения задачи минимального k-разреза.
+
В качестве алгоритма для кластеризации предлагается использовать вероятностный алгоритм типа Монте-Карло, придуманный Каргером для решения задачи минимального k-разреза.
Введем дополнительную процедуру, для описания данного алгоритма. Эта процедура представляет собой построение дендрограммы до заранее заданного уровня.
Введем дополнительную процедуру, для описания данного алгоритма. Эта процедура представляет собой построение дендрограммы до заранее заданного уровня.
Строка 36: Строка 36:
<br>
<br>
Процесс: <br>
Процесс: <br>
-
Пока |V_G | ≥m <br>
+
Пока <tex>|V_G | \geq m</tex> <br>
-
Выбирается произвольное ребро (u,v)∈E_G <br>
+
:Выбирается произвольное ребро <tex>(u,v) \in E_G</tex> <br>
-
G←G/{u,v} <br>
+
:<tex>G \leftarrow G/\{u,v\}</tex> <br>
Вернуть <tex>G</tex>.
Вернуть <tex>G</tex>.
Строка 51: Строка 51:
Процесс:
Процесс:
Инициализация: <tex>i=1</tex>. <br>
Инициализация: <tex>i=1</tex>. <br>
-
Повторять пока <tex>i≤r</tex> <br>
+
Повторять пока <tex>i \leq r</tex> <br>
-
Слияние <tex>(G,k)</tex> <br>
+
:Слияние <tex>(G,k)</tex> <br>
-
<tex>i=i+1</tex> <br>
+
:Количество оставшихся ребер представляет собой функционал <tex>f_i(G)=C_i </tex> <br>
-
Из получившихся дендрограмм выбираем min┬i⁡〖C_i 〗
+
:<tex>i=i+1</tex> <br>
 +
Из получившихся дендрограмм выбираем <tex>\min_i C_i</tex>
-
Здесь во внутреннем цикле происходит построение дендрограммы. Поскольку алгоритм сливает вершины совершенно произвольно, то мы не можем гарантировать нахождение оптимального решения. Однако можно оценить вероятность этого.
+
Здесь во внутреннем цикле (процедура Слияние) происходит построение дендрограммы. Поскольку алгоритм сливает вершины совершенно произвольно, то мы не можем гарантировать нахождение оптимального решения. Однако можно оценить вероятность этого.
<br>
<br>
-
::<tex>P(succeed)=P(C_i=C_{opt})\geq\frac1{\dbinom{n+k-2}{2k-2}}</tex>
+
::<tex>P(succeed)=P(C_i=C_{opt})\geq\frac1{\binom{n+k-2}{2k-2}}</tex>
Внешний цикл представляет собой процедуру вероятностной амплификации. Повторив внутренний цикл <tex>r</tex> раз мы получим, что
Внешний цикл представляет собой процедуру вероятностной амплификации. Повторив внутренний цикл <tex>r</tex> раз мы получим, что
<br>
<br>
-
::<tex>P(succeed) \geq 1 - (1-\frac1{\dbinom{n+k-2}{2k-2}})^r</tex>,
+
::<tex>P(succeed) \geq 1 - (1-\frac1{С_{n+k-2^{2k-2}}})^r</tex>,
-
откуда для <tex>r=\dbinom{n+k-2}{2k-2} \ln n</tex> выполнено <tex>P(succeed) \geq 1-\frac1n</tex>.
+
откуда для <tex>r=\binom{n+k-2}{2k-2} \ln n</tex> выполнено <tex>P(succeed) \geq 1-\frac1n</tex>.
<br>
<br>
Получаем, что поскольку <tex>r=n^{2k-2} \ln n</tex>, трудоемкость алгоритма составляет <tex>O(rn^2)=O(n^{2k} \log n)</tex>.
Получаем, что поскольку <tex>r=n^{2k-2} \ln n</tex>, трудоемкость алгоритма составляет <tex>O(rn^2)=O(n^{2k} \log n)</tex>.
Строка 73: Строка 74:
== Вычислительный эксперимент ==
== Вычислительный эксперимент ==
-
Вычислительный эксперимент будет проведен на ряде модельных графов. Представлены графы с различным числом вершин, результаты кластеризации данных графов, полученные рассматриваемым алгоритмом, и получены графики зависимости времени работы и качества работы алгоритма от числа вершин в графе.
+
[[Изображение:MinValueDependence.jpg|thumb|right]]
 +
[[Изображение:OriginalGraph.jpg‎|thumb|left]]
 +
[[Изображение:3clusteredGraph.jpg|thumb|left]]
 +
[[Изображение:4clusteredGraph.jpg|thumb|left]]
 +
[[Изображение:PSucDependence.jpg|thumb|right]]
 +
Вычислительный эксперимент был проведен в несколько этапов.
 +
 +
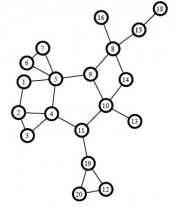
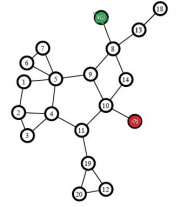
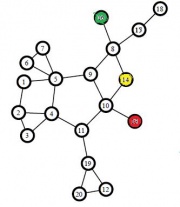
Вначале алгоритм был протестирован на графах с малым количеством вершин и заранее известной величиной k-разреза. Исходный граф и результаты работы алгоритма можно наблюдать на рисунках слева.
 +
 +
Оказалось, что данный алгоритм с высокой точностью находит минимум искомого функционала. Минус заключается в том, что сама форма рассматриваемого функционала приводит к тому, что алгоритм склонен к кластеризации висячих вершин в качестве отдельных кластеров. Избавиться от этого можно модифицировав целевой оптимизационный функционал, чтобы он учитывал не только количество ребер между кластерами, но и количество ребер или вершин внутри кластера.
 +
 +
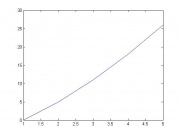
После этого было проведено исследование предполагаемого числа кластеров в графе, в который каждое ребро входит с заранее известной вероятностью. Выяснилось, что для плотных графов, в которых данная вероятность равна 1/2, исследуемый функционал растет практически линейно с ростом числа кластеров. График подобной зависимости находится справа сверху. Можно сделать выводы о том, что если нет заранее известных предпосылок для разделения графа на большое число кластеров, то для изучения структуры графа будет достаточно разделения на 3 или 4 кластера.
 +
 +
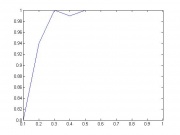
Поскольку зависимость времени работы графа от числа вершин и количества кластеров экспоненциальна (<tex>O(n^{2k} \log n)</tex>), то практическое применение данного алгоритма ограничено графами с количеством вершин порядка <tex>10^2</tex> и количеством кластеров порядка 5. Было проведено исследование зависимости вероятности нахождения глобального минимума в зависимости от количества итераций <tex>r</tex>. Типичный график подобной зависимости находится справа внизу. Видно, что для достижения приемлемого приближения глобального минимума рассматриваемого функционала на практике требуется не менее трети от теоретически необходимого количества итераций, что подтверждает полученные асимптотические оценки.
 +
 +
Резюмируя, из полученных расчетов можно сделать следующие выводы:
 +
# рассматриваемый алгоритм обладает избыточной склонностью к кластеризации отдельных висячих вершин
 +
#* эту проблему можно решить модификацией минимизируемого функционала
 +
#* структура алгоритма позволяет легко произвести подобную модификацию
 +
# большая трудоемкость данного алгоритма не позволяет использовать его для кластеризации графов с количеством вершин порядка <tex>10^3</tex>
 +
#* эту проблему можно решить используя различные приближенные жадные алгоритмы
 +
#* разработка данных жадных алгоритмов является открытой проблемой
 +
 +
== Исходный код ==
== Исходный код ==
== Исходный код ==
 +
[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/MIPT2006-2010OldProj/Kozlov2010Karger/ Kozlov2010Karger]
== Литература ==
== Литература ==
-
{{Задание|Козлов Илья|В.В.Стрижов|9 мая 2010|Volokno|Strijov}}
+
{{ЗаданиеВыполнено|Козлов Илья|В.В.Стрижов|9 мая 2010|Volokno|Strijov}}
[[Категория:Практика и вычислительные эксперименты]]
[[Категория:Практика и вычислительные эксперименты]]
 +
* Karger D. Global min-cuts in RNC and other ramifications of a simple mincut algorithm // Proc. of the 4-th ACM-SIAM Symp. on Discrete Algorithms. – 1993. – P. 21-30.
 +
* Karger D., Stein C. A new approach to the minimum cut problem // JACM, 43. – 1996. – P. 601-640.
 +
* Kumar V., Tan P., Steinbach M. Introduction to Data Mining. – Addison-Wesley, 2005. – 769 pp.
 +
* Nagamochi H., Ibaraki T. Computing edge connectivity in multigraphs and capacitated graphs // SIAM J. Disc. Math., 5. – 1992. – P. 54-66.

Текущая версия

Содержание

Аннотация

Данная работа посвящена решению задачи кластеризации. Рассматривается задача кластеризации на графах, на которых не задана метрика. Подобная задача может встретиться, например, при анализе групп знакомств в социальных сетях. Для ее решения предлагается использовать вероятностный алгоритм построения дендрограммы.

Постановка задачи

Пусть задан граф G(V,E,w): \; |V|=n, \; |E|=m (V – множество вершин графа, E – множество ребер, w:E\rightarrow\mathbb{R}^+ – весовая функция) и целое число k.

Задача кластеризации заключается в поиске разбиения V на k непересекающихся подмножеств (V=\{V_1,\dots,V_k\}), с минимизацией заданного функционала f(G). В качестве такого функционала будем рассматривать сумму весов ребер между подмножествами, т.е.

f(G)=\sum_{i=1}^{k-1} \sum_{j=i+1}^k \sum_{\substack{v_1\in V_i \\ v_2\in V_j}} w(\{v_1,v_2\})\rightarrow\min

Введем ряд определений, которыми будем пользоваться в дальнейшем.
Определение. Вероятность, превышающую 1-\frac1n, будем называть высокой.
Определение. Вероятностный алгоритм, получающий на вход данные оптимизационной задачи и параметр \varepsilon>0, который за полиномиальное время с высокой вероятностью получает решение, не более чем в (1+\varepsilon) раз превышающее оптимальное, будем называть полиномиальной рандомизированной аппроксимационной схемой (PRAS).
Определение. Если PRAS находит оптимальное решение с высокой вероятностью для любого \varepsilon>0, то такой алгоритм будем называть вероятностным алгоритмом типа Монте-Карло.

В дальнейшем граф G будем считать связным, а веса ребер – единичными. Несколько слов о модификации алгоритма для решения задачи в случае взвешенного графа будет сказано в следующем разделе.

Первое условие не накладывает никаких дополнительных ограничений, поскольку в случае несвязного графа можно каждую отдельную компоненту связности рассматривать в качестве одного из кластеров.

Второе условие возникает из конструкции алгоритма и приводит к тому, что минимизируемый функционал f(G) будет представлять собой число ребер между кластерами. Для того чтобы рассмотреть задачу в более общем случае потребуется дерандомизация исследуемого алгоритма, что приведет к возрастанию его трудоемкости.

Заметим, что рассматривается задача с заранее заданным число кластеров. Подбор оптимального значения числа k можно в дальнейшем осуществить простым перебором.

Алгоритм

В качестве алгоритма для кластеризации предлагается использовать вероятностный алгоритм типа Монте-Карло, придуманный Каргером для решения задачи минимального k-разреза.

Введем дополнительную процедуру, для описания данного алгоритма. Эта процедура представляет собой построение дендрограммы до заранее заданного уровня.

Слияние (G,m)
Вход: граф G, число m.
Выход: гиперграф G.
Процесс:
Пока |V_G | \geq m

Выбирается произвольное ребро (u,v) \in E_G
G \leftarrow G/\{u,v\}

Вернуть G.

Здесь и далее граф задается симметричной матрицей инцидентности, и все операции слияния вершин реализованы как работа со строками и столбцами этой матрицы. Функционал f(G) тогда равен половине суммы всех недиагональных элементов матрицы. Собственно алгоритм описывается следующим образом:

Алгоритм Каргера
Вход: граф G, число k, число r - количество итераций алгоритма.
Выход: k-разрез G.
Процесс: Инициализация: i=1.
Повторять пока i \leq r

Слияние (G,k)
Количество оставшихся ребер представляет собой функционал f_i(G)=C_i
i=i+1

Из получившихся дендрограмм выбираем \min_i C_i

Здесь во внутреннем цикле (процедура Слияние) происходит построение дендрограммы. Поскольку алгоритм сливает вершины совершенно произвольно, то мы не можем гарантировать нахождение оптимального решения. Однако можно оценить вероятность этого.

P(succeed)=P(C_i=C_{opt})\geq\frac1{\binom{n+k-2}{2k-2}}

Внешний цикл представляет собой процедуру вероятностной амплификации. Повторив внутренний цикл r раз мы получим, что

P(succeed) \geq 1 - (1-\frac1{С_{n+k-2^{2k-2}}})^r,

откуда для r=\binom{n+k-2}{2k-2} \ln n выполнено P(succeed) \geq 1-\frac1n.
Получаем, что поскольку r=n^{2k-2} \ln n, трудоемкость алгоритма составляет O(rn^2)=O(n^{2k} \log n).


Так как каждый внешний цикл алгоритма выполняется независимо от остальных, алгоритм Каргера можно модифицировать и уменьшить время его работы, используя параллельные вычисления. Если задействовать n^{2k-2} \ln n процессоров и выполнить на каждом из них по одному вычислению внешнего цикла алгоритма, то трудоемкость такого распределенного алгоритма будет O(n^2). Таким образом, в зависимости от существующих мощностей можно подобрать оптимальное соотношение между количеством используемых процессоров и трудоемкостью получающейся задачи.

Еще одно направление модификации алгоритма позволяет рассмотреть случай взвешенного графа. Для этого требуется ввести дополнительный функционал, который перед слиянием вершин будет давать оценки, чтобы сливать только те вершины, ребра между которыми наиболее похожи на межкластерные.

Вычислительный эксперимент

Вычислительный эксперимент был проведен в несколько этапов.

Вначале алгоритм был протестирован на графах с малым количеством вершин и заранее известной величиной k-разреза. Исходный граф и результаты работы алгоритма можно наблюдать на рисунках слева.

Оказалось, что данный алгоритм с высокой точностью находит минимум искомого функционала. Минус заключается в том, что сама форма рассматриваемого функционала приводит к тому, что алгоритм склонен к кластеризации висячих вершин в качестве отдельных кластеров. Избавиться от этого можно модифицировав целевой оптимизационный функционал, чтобы он учитывал не только количество ребер между кластерами, но и количество ребер или вершин внутри кластера.

После этого было проведено исследование предполагаемого числа кластеров в графе, в который каждое ребро входит с заранее известной вероятностью. Выяснилось, что для плотных графов, в которых данная вероятность равна 1/2, исследуемый функционал растет практически линейно с ростом числа кластеров. График подобной зависимости находится справа сверху. Можно сделать выводы о том, что если нет заранее известных предпосылок для разделения графа на большое число кластеров, то для изучения структуры графа будет достаточно разделения на 3 или 4 кластера.

Поскольку зависимость времени работы графа от числа вершин и количества кластеров экспоненциальна (O(n^{2k} \log n)), то практическое применение данного алгоритма ограничено графами с количеством вершин порядка 10^2 и количеством кластеров порядка 5. Было проведено исследование зависимости вероятности нахождения глобального минимума в зависимости от количества итераций r. Типичный график подобной зависимости находится справа внизу. Видно, что для достижения приемлемого приближения глобального минимума рассматриваемого функционала на практике требуется не менее трети от теоретически необходимого количества итераций, что подтверждает полученные асимптотические оценки.

Резюмируя, из полученных расчетов можно сделать следующие выводы:

  1. рассматриваемый алгоритм обладает избыточной склонностью к кластеризации отдельных висячих вершин
    • эту проблему можно решить модификацией минимизируемого функционала
    • структура алгоритма позволяет легко произвести подобную модификацию
  2. большая трудоемкость данного алгоритма не позволяет использовать его для кластеризации графов с количеством вершин порядка 10^3
    • эту проблему можно решить используя различные приближенные жадные алгоритмы
    • разработка данных жадных алгоритмов является открытой проблемой

Исходный код

Исходный код

Kozlov2010Karger

Литература

Данная статья была создана в рамках учебного задания.
Студент: Козлов Илья
Преподаватель: В.В.Стрижов
Срок: 9 мая 2010


В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

  • Karger D. Global min-cuts in RNC and other ramifications of a simple mincut algorithm // Proc. of the 4-th ACM-SIAM Symp. on Discrete Algorithms. – 1993. – P. 21-30.
  • Karger D., Stein C. A new approach to the minimum cut problem // JACM, 43. – 1996. – P. 601-640.
  • Kumar V., Tan P., Steinbach M. Introduction to Data Mining. – Addison-Wesley, 2005. – 769 pp.
  • Nagamochi H., Ibaraki T. Computing edge connectivity in multigraphs and capacitated graphs // SIAM J. Disc. Math., 5. – 1992. – P. 54-66.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BB%D0%B0%D1%81%D1%82%D0%B5%D1%80%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2_%D0%B1%D0%B5%D0%B7_%D0%B8%D1%81%D0%BF%D0%BE%D0%BB%D1%8C%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты