Метод потенциального бустинга
Материал из MachineLearning.
(Новая: Метод потенциального бустинга - алгоритм классификации, использующий процедуру [[...) |
(→Идея метода) |
||
| (11 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
Метод потенциального бустинга - [[алгоритм]] [[классификация|классификации]], использующий процедуру [[бустинг|бустинга]] для обучения классификатора - [[метод потенциальных функций|метода потенциальных функций]]. | Метод потенциального бустинга - [[алгоритм]] [[классификация|классификации]], использующий процедуру [[бустинг|бустинга]] для обучения классификатора - [[метод потенциальных функций|метода потенциальных функций]]. | ||
| + | |||
| + | ==Идея метода== | ||
| + | Бустинг - метод построения композиции классификаторов, которая последовательно обучает базовые классификаторы, каждый раз стараясь исправить ошибки, допускаемые всеми предыдущими классификаторами. | ||
| + | |||
| + | Идея метода потенциальных функций состоит в том, чтобы в пространстве объектов каждый объект создавал потенциальное поле со своим зарядом, соответствующим его классу (по аналогии с электростатикой). В качестве функции потенциалов можно брать любую функцию, достигающую в центре своего максимума и убывающую при отдалении от центра. Классификатором становится совокупность всех потенциалов - объект причисляется к тому классу, представители которого дают наибольший суммарный потенциал в этом объекте. | ||
| + | |||
| + | Главной идеей метода потенциального бустинга является построение классификатора, которое является композицией базовых классификаторов - потенциальных функций. Построение композиции методом бустинга позволяет устранить типичные недостатки [[метод потенциальных функций|метода потенциальных функций]]: медленная сходимость алгоритма, отсутствие настройки или очень грубая настройка параметров потенциалов, зависимость результата от порядка выбора объектов обучающей выборки. | ||
| + | |||
| + | ==Описание алгоритма== | ||
| + | ===Постановка проблемы=== | ||
| + | ====Задача классификации==== | ||
| + | |||
| + | Пусть <tex>X</tex> — множество описаний объектов (все описания - m-мерные числовые векторы), | ||
| + | <tex>Y</tex>={1,-1} — множество номеров классов. | ||
| + | Существует неизвестная ''целевая зависимость'' — отображение | ||
| + | <tex>y^{*}:\; X\to Y</tex>, | ||
| + | значения которой известны только на объектах конечной [[выборка|обучающей выборки]] | ||
| + | <tex>X^l = \{(x_1,y_1),\dots,(x_n,y_n)\}</tex>. | ||
| + | Требуется построить [[алгоритм]] | ||
| + | <tex>B:\; X\to Y</tex>, | ||
| + | способный классифицировать произвольный объект | ||
| + | <tex>x \in X</tex>. | ||
| + | |||
| + | ====Задача потенциального бустинга ==== | ||
| + | Введем функцию вида: <br /> | ||
| + | <tex>f(x,h)</tex> = exp(<tex>-\sum^{m}_{i=1}{(\frac{x_j}{h_j})^2})</tex> - потенциальная функция с центром в нуле и вектором ширины <tex> h=(h_1,...,h_m)</tex>, где <tex>h_i</tex> - характеризует ширину потенциала по i-ой координате. | ||
| + | Введем семейство базовых вещественнозначных классификаторов: <br /> | ||
| + | <tex>b_t(x) = s_tf(x-a_t,h_t)</tex> , где <tex>s_t</tex> = ±1 - тип t-го потенциала, <tex>a_t=(a_1,...,a_m)</tex> - координаты центра t-го потенциала, <tex>h_t</tex> - ширина t-го потенциала. Потенциалы типа +1 имеют только положительные значения, потенциалы типа -1 имеют только отрицательные значения. <br /> | ||
| + | Задача потенциального бустинга состоит в обучении композиции базовых классификаторов как их линейной комбинации: <br /> | ||
| + | <tex>B(x)</tex>=sign(<tex>\sum^{T}_{t=1}{\alpha_tb_t(x)}</tex>) , где <tex>T</tex> - число базовых классификаторов, <tex>\alpha_1,...,\alpha_T</tex> - коэффициенты этих классификаторов. <br /> | ||
| + | Если <tex>B(x)</tex> = 1 , то объект причисляется к классу 1, иначе - к классу -1. <br /> | ||
| + | Введем отступ композиции на объекте <tex>x_i</tex> : <br /> | ||
| + | <tex>M_T(x_i) = y_i\sum^{T}_{t=1}{\alpha_tb_t(x_i)}</tex> <br /> | ||
| + | |||
| + | Отрицательное значение отступа показывает ошибку предсказания композиции на объекте : чем больше по абсолютному значению – тем сильнее композиция ошибается. Положительное значение отступа показывает, что композиция правильно распознает объект: чем больше значение - тем увереннее композиция распознает его. <br /> | ||
| + | |||
| + | |||
| + | ===Схема алгоритма=== | ||
| + | 1. <tex>M_0(x_i):=0</tex> <br /> | ||
| + | 2. Для <tex> t = 1,...,T: </tex> <br /> | ||
| + | a. <tex>w_i:=</tex>exp(<tex>-M</tex><sub>t-1</sub><tex>(x_i)</tex>) <br /> | ||
| + | b. Решается задача оптимизации: <tex>\sum^{n}_{i=1}{w_iy_ib_t(x_i)} \rightarrow max </tex> по <tex> a_t\in X , h_t</tex>≥0, <tex> s_t = 1,-1</tex>. <br /> | ||
| + | c. Рещается задача одномерной оптимизации: <tex>\sum^{n}_{i=1}{w_i exp(-\alpha_t b_t(x_i)y_i)} \rightarrow min </tex> по <tex>alpha_t</tex>>0 <br /> | ||
| + | d. Значения отступов композиции обновляются: <tex>M_t(x_i):=M</tex><sub>t-1</sub>(<tex>x_i</tex>)<tex>+\alpha_t b_t(x_i)y_i</tex> <br /> | ||
| + | 3. Строится конечная композиция: <tex>B(x)</tex>=sign(<tex>\sum^{T}_{t=1}{\alpha_tb_t(x)}</tex>) <br /> | ||
| + | |||
| + | |||
| + | |||
| + | == См. также == | ||
| + | |||
| + | * [[Метод потенциальных функций]] | ||
| + | * [[Метрический классификатор]] | ||
| + | * [[Бустинг]] | ||
| + | * [[Алгоритм AdaBoost]] | ||
| + | |||
| + | |||
| + | {{Задание|Djulustan|Константин Воронцов|30 июня 2013}} | ||
| + | |||
| + | |||
| + | |||
| + | [[Категория:Алгоритмические композиции]] | ||
| + | [[Категория:Метрические алгоритмы классификации]] | ||
| + | [[Категория:Непроверенные учебные задания]] | ||
Текущая версия
Метод потенциального бустинга - алгоритм классификации, использующий процедуру бустинга для обучения классификатора - метода потенциальных функций.
Содержание |
Идея метода
Бустинг - метод построения композиции классификаторов, которая последовательно обучает базовые классификаторы, каждый раз стараясь исправить ошибки, допускаемые всеми предыдущими классификаторами.
Идея метода потенциальных функций состоит в том, чтобы в пространстве объектов каждый объект создавал потенциальное поле со своим зарядом, соответствующим его классу (по аналогии с электростатикой). В качестве функции потенциалов можно брать любую функцию, достигающую в центре своего максимума и убывающую при отдалении от центра. Классификатором становится совокупность всех потенциалов - объект причисляется к тому классу, представители которого дают наибольший суммарный потенциал в этом объекте.
Главной идеей метода потенциального бустинга является построение классификатора, которое является композицией базовых классификаторов - потенциальных функций. Построение композиции методом бустинга позволяет устранить типичные недостатки метода потенциальных функций: медленная сходимость алгоритма, отсутствие настройки или очень грубая настройка параметров потенциалов, зависимость результата от порядка выбора объектов обучающей выборки.
Описание алгоритма
Постановка проблемы
Задача классификации
Пусть — множество описаний объектов (все описания - m-мерные числовые векторы),
={1,-1} — множество номеров классов.
Существует неизвестная целевая зависимость — отображение
,
значения которой известны только на объектах конечной обучающей выборки
.
Требуется построить алгоритм
,
способный классифицировать произвольный объект
.
Задача потенциального бустинга
Введем функцию вида:
= exp(
- потенциальная функция с центром в нуле и вектором ширины
, где
- характеризует ширину потенциала по i-ой координате.
Введем семейство базовых вещественнозначных классификаторов:
, где
= ±1 - тип t-го потенциала,
- координаты центра t-го потенциала,
- ширина t-го потенциала. Потенциалы типа +1 имеют только положительные значения, потенциалы типа -1 имеют только отрицательные значения.
Задача потенциального бустинга состоит в обучении композиции базовых классификаторов как их линейной комбинации:
=sign(
) , где
- число базовых классификаторов,
- коэффициенты этих классификаторов.
Если = 1 , то объект причисляется к классу 1, иначе - к классу -1.
Введем отступ композиции на объекте :
Отрицательное значение отступа показывает ошибку предсказания композиции на объекте : чем больше по абсолютному значению – тем сильнее композиция ошибается. Положительное значение отступа показывает, что композиция правильно распознает объект: чем больше значение - тем увереннее композиция распознает его.
Схема алгоритма
1.:=0)
2. Для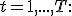
a.exp(
t-1
)
b. Решается задача оптимизации:по
≥0,
.
c. Рещается задача одномерной оптимизации:по
>0
d. Значения отступов композиции обновляются:t-1(
)
y_i)
3. Строится конечная композиция:=sign(
)
См. также
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |

